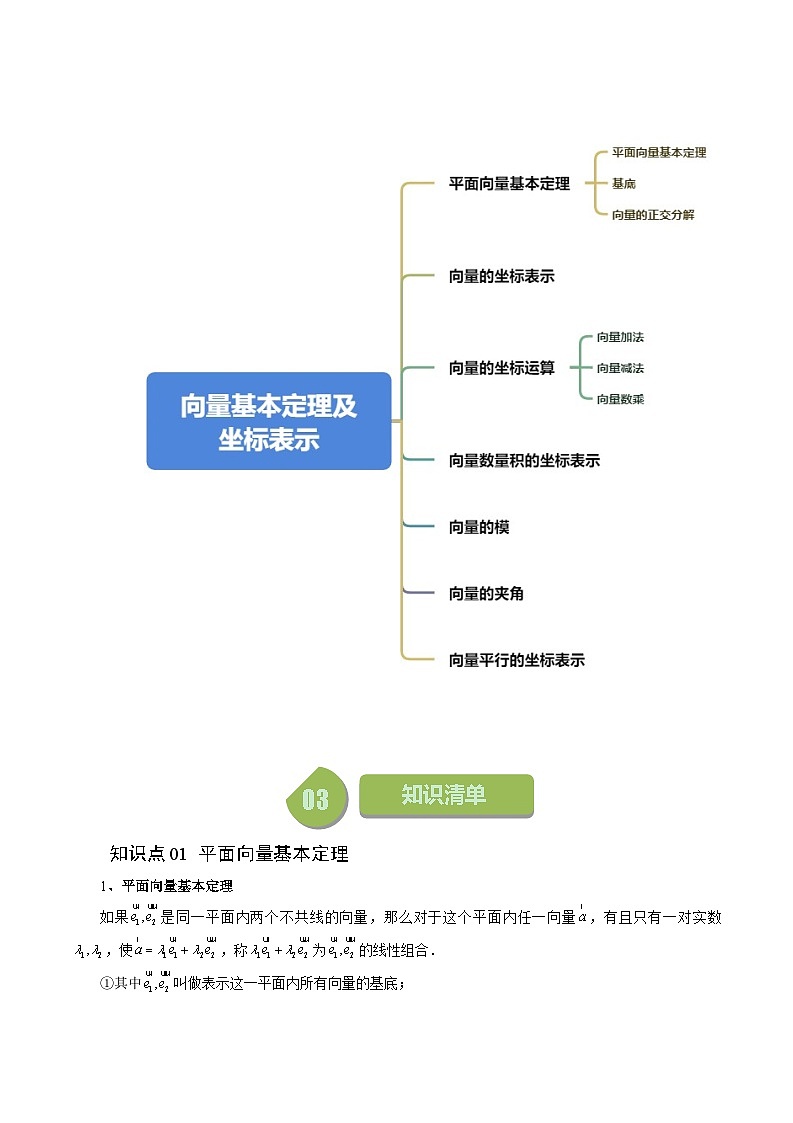
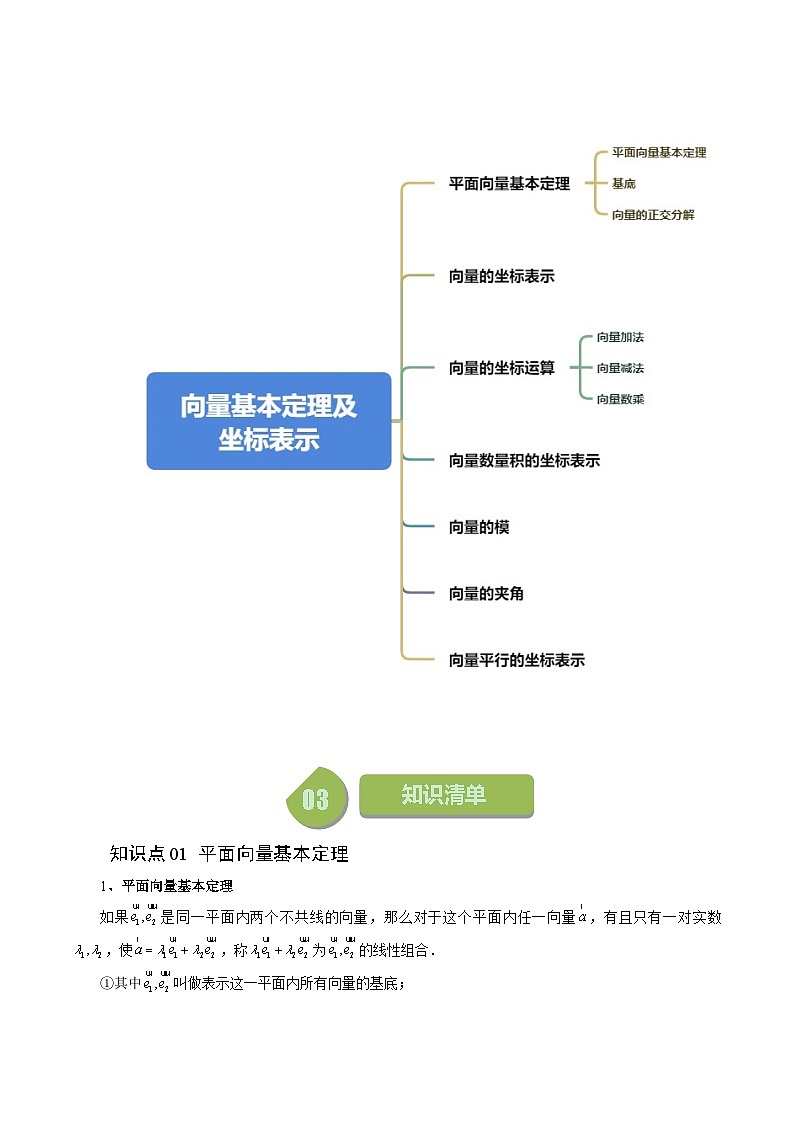
高中数学苏教版 (2019)必修 第二册9.3 向量基本定理及坐标表示精练

这是一份高中数学苏教版 (2019)必修 第二册9.3 向量基本定理及坐标表示精练，文件包含2023-2024学年高一数学下册同步学与练苏教版-93向量基本定理及坐标表示十三大题型原卷版docx、2023-2024学年高一数学下册同步学与练苏教版-93向量基本定理及坐标表示十三大题型解析版docx等2份试卷配套教学资源，其中试卷共66页， 欢迎下载使用。


知识点01 平面向量基本定理
1、平面向量基本定理
如果是同一平面内两个不共线的向量，那么对于这个平面内任一向量，有且只有一对实数，使，称为的线性组合．
①其中叫做表示这一平面内所有向量的基底；
②平面内任一向量都可以沿两个不共线向量的方向分解为两个向量的和，并且这种分解是唯一的．
这说明如果且，那么．
③当基底是两个互相垂直的单位向量时，就建立了平面直角坐标系，因此平面向量基本定理实际上是平面向量坐标表示的基础．
知识点诠释：
平面向量基本定理的作用：平面向量基本定理是建立向量坐标的基础，它保证了向量与坐标是一一对应的，在应用时，构成两个基底的向量是不共线向量．
2、如何使用平面向量基本定理
平面向量基本定理反映了平面内任意一个向量可以写成任意两个不共线的向量的线性组合．
（1）由平面向量基本定理可知，任一平面直线形图形，都可以表示成某些向量的线性组合，这样在解答几何问题时，就可以先把已知和结论表示为向量的形式，然后通过向量的运算，达到解题的目的．
（2）在解具体问题时，要适当地选取基底，使其他向量能够用基底来表示．选择了不共线的两个向量、，平面上的任何一个向量都可以用、唯一表示为=+，这样几何问题就转化为代数问题，转化为只含有、的代数运算．
【即学即练1】（2024·河南省直辖县级单位·高一河南省济源第一中学校考阶段练习）如图，在中，，P是线段BD上一点，若，则实数m的值为（ ）

A．B．C．D．
【答案】A
【解析】∵，∴，
又，∴，
∵B，P，D三点共线，∴，∴.
故选：A.
知识点02 平面向量的坐标表示
1、正交分解
把一个向量分解为两个互相垂直的向量，叫做把向量正交分解．
知识点诠释：
如果基底的两个基向量、互相垂直，则称这个基底为正交基底，在正交基底下分解向量，叫做正交分解，事实上，正交分解是平面向量基本定理的特殊形式．
2、平面向量的坐标表示
如图，在平面直角坐标系内，分别取与轴、轴方向相同的两个单位向量、作为基底，对于平面上的一个向量，由平面向量基本定理可知，有且只有一对实数，使得=．这样，平面内的任一向量都可由唯一确定，我们把有序数对叫做向量的（直角）坐标，记作=，x叫做在轴上的坐标，叫做在轴上的坐标．把叫做向量的坐标表示．给出了平面向量的直角坐标表示，在平面直角坐标系内，每一个平面向量都可以用一有序数对唯一表示，从而建立了向量与实数的联系，为向量运算数量化、代数化奠定了基础，沟通了数与形的联系．
知识点诠释：
（1）由向量的坐标定义知，两向量相等的充要条件是它们的坐标相等，即且，其中，．
（2）要把点的坐标与向量坐标区别开来．相等的向量的坐标是相同的，但始点、终点的坐标可以不同．比如，若，，则；若，，则，，显然A、B、C、D四点坐标各不相同．
（3）在直角坐标系中有双重意义，它既可以表示一个固定的点，又可以表示一个向量．
【即学即练2】（2024·全国·高一随堂练习）如图，设为一组标准正交基，用这组标准正交基分别表示向量，，，，并求出它们的坐标．

【解析】由图可知：
，对应坐标为；
，对应坐标为；
，对应坐标为；
，对应坐标为.
知识点03 平面向量的坐标运算
1、平面向量坐标的加法、减法和数乘运算
2、如何进行平面向量的坐标运算
在进行平面向量的坐标运算时，应先将平面向量用坐标的形式表示出来，再根据向量的直角坐标运算法则进行计算．在求一个向量时，可以首先求出这个向量的起点坐标和终点坐标，再运用终点坐标减去起点坐标得到该向量的坐标．求一个点的坐标，可以转化为求该点相对于坐标原点的位置向量的坐标．但同时注意以下几个问题：
（1）点的坐标和向量的坐标是有区别的，平面向量的坐标与该向量的起点、终点坐标有关，只有起点在原点时，平面向量的坐标与终点的坐标才相等．
（2）进行平面向量坐标运算时，先要分清向量坐标与向量起点、终点的关系．
（3）要注意用坐标求向量的模与用两点间距离公式求有向线段的长度是一样的．
（4）要清楚向量的坐标与表示该向量的有向线段的起点、终点的具体位置无关，只与其相对位置有关．
【即学即练3】（2024·山西运城·高一统考期末）已知，，点P是线段MN的一个三等分点且靠近点M，则点P的坐标为 ．
【答案】
【解析】由题可知，
设，则，
，，
∴.
故答案为：.
知识点04 平面向量平行（共线）的坐标表示
1、平面向量平行（共线）的坐标表示
设非零向量，则，即，或．
知识点诠释：
若，则不能表示成因为分母有可能为0．
2、三点共线的判断方法
判断三点是否共线，先求每两点对应的向量，然后再按两向量共线进行判定，即已知
，，
若则A，B，C三点共线．
【即学即练4】（2024·江苏无锡·高一江苏省太湖高级中学校考阶段练习）向量，，，若，，三点共线，则的值为（ ）
A．或B．或C．或-11D．或
【答案】A
【解析】由，，，
得，，
又，，三点共线，
则，
即，解得或，
故选：A.
知识点05 向量数量积的坐标表示
1、已知两个非零向量，，
2、设，则或
3、如果表示向量的有向线段的起点和终点的坐标分别为、，那么（平面内两点间的距离公式）．
【即学即练5】（2024·全国·高一随堂练习）已知，，且，则 ．
【答案】1
【解析】,解得，
故答案为:1.
题型一：平面向量基本定理的理解
【例1】（2024·高一课时练习）已知，是不共线的非零向量，则以下向量可以作为基底的是（ ）
A．，B．，
C．，D．，
【答案】C
【解析】对于A：零向量与任意向量均共线，所以此两个向量不可以作为基底；
对于B：因为，，所以，所以此两个向量不可以作为基底；
对于C：设，即，则，所以无解，所以此两个向量不共线，可以作为一组基底；
对于D：设，，所以，所以此两个向量不可以作为基底；
故选：C.
【变式1-1】（2024·黑龙江齐齐哈尔·高一齐齐哈尔中学校考期中）设是平面内所有向量的一个基底，则下列不能作为基底的是（ ）
A．和B．和
C．和D．和
【答案】C
【解析】对于A，令，则，不存在，，不共线，可以作为基底，A错误；
对于B，令，则，不存在，，不共线，可以作为基底，B错误；
对于C，，
和共线，不能作为一组基底，C正确；
对于D，令，则，不存在，，不共线，可以作为基底，D错误.
故选：C.
【变式1-2】（2024·高一课时练习）设是平面内所有向量的一组基底，则下列四组向量中，不能作为基底的是（ ）
A． 和 B．和
C． 和 D．和
【答案】B
【解析】是平面内所有向量的一组基底，所以不共线；
所以和不共线，和不共线，和不共线；
所以选项A,C,D都可以作为基底；
B中，，
所以和共线，不能作为基底．
故选：B
【变式1-3】（2024·山西·高一校联考阶段练习）如果表示平面内所有向量的一个基底，那么下列四组向量，不能作为一个基底的是（ ）
A．、B．、
C．、D．、
【答案】C
【解析】对于A选项，设，
因为、不共线，则，显然不成立，A中的两个向量可作一个基底；
对于B选项，设，
因为、不共线，则，显然不成立，B中的两个向量可作一个基底；
对于C选项，因为，C中的两个向量不能作一个基底；
对于D选项，设，
因为、不共线，则，显然不成立，D中的两个向量可作一个基底.
故选：C.
【方法技巧与总结】
考查两个向量是否能构成基底，主要看两向量是否不共线．此外，一个平面的基底一旦确定，那么平面上任意一个向量都可以由这个基底唯一线性表示出来．
题型二：用基底表示向量
【例2】（2024·全国·高一假期作业）如图，在平行四边形中，是的中点，和相交于点． 记 ，，则（ ）

A．B．
C．D．
【答案】A
【解析】在平行四边形中，和相交于点，
所以，又是的中点，
所以，所以，
所以.
故选：A
【变式2-1】（2024·陕西·高一校联考期中）如图，在中，设，，，，则（ ）

A．B．
C．D．
【答案】D
【解析】由题意,
故选：D．
【变式2-2】（2024·安徽芜湖·高一安徽省无为襄安中学校考期中）在中，为边上的中线，为的中点，则等于（ ）
A．B．C．D．
【答案】B
【解析】因为，
所以．
故选：B
【方法技巧与总结】
平面向量基本定理的作用以及注意点
（1）根据平面向量基本定理，任何一个基底都可以表示任意向量．用基底表示向量，实质上是利用三角形法则或平行四边形法则，进行向量的线性运算．
（2）基底的选取要灵活，必要时可以建立方程或方程组，通过方程求出要表示的向量．
题型三：平面向量基本定理的应用
【例3】（2024·全国·高一随堂练习）如图所示，中，AQ为边BC的中线，，，，，其中，，，．

(1)当时，用向量，表示；
(2)证明：为定值．
【解析】（1）当时，，
因为AQ为边BC的中线，
所以，
所以．
（2）由（1）可知，
所以．
而，，，
所以，
即，
整理可得，
而，是不共线向量，所以，
两式相加可得，是定值,证毕．
【变式3-1】（2024·海南·高一校考期末）如图，在中，是边上的中线，为的中点．

(1)用，表示；
(2)用，表示．
【解析】（1）因为是边上的中线，
所以.
（2）因为为的中点，
所以.
【变式3-2】（2024·河北邢台·高一邢台市第二中学校考阶段练习）如图，四边形ABCD是平行四边形，点E，F分别为CD，AD的中点

(1)以，为基底，分别表示向量，；
(2)以，为基底，表示向量.
【解析】（1）因为为DC中点，则，
F为AD中点，则；
（2）注意到，
又为DC中点，则，
F为AD中点，则，
则，
，
则.
【变式3-3】（2024·广西钦州·高一校考期末）如图，在中，，，BE与AD相交于点M．

(1)用，表示，；
(2)若，求的值．
【解析】（1）因为，所以，
所以．
因为，所以，
所以．
（2）因为A，M，D三点共线，所以．
因为，所以，即．
因为B，M，E三点共线，所以．
因为，所以．
因为，所以，解得，
从而，，故．
【变式3-4】（2024·高一校考单元测试）如图所示，已知点是的重心.

(1)求；
(2)若过的重心，且，，，，求证：.
【解析】（1）如图所示，延长交于点，则是的中点，
∴，
∵是的重心，∴，∴；
（2）∵是边的中点，∴，
又∵是的重心， ∴，
∴，
而，
∵、、三点共线，∴有且只有一个实数，使得，
∴，∴，
∵与不共线，∴且消去，得.
【方法技巧与总结】
若直接利用基底表示向量比较困难，可设出目标向量并建立其与基底之间满足的二元关系式，然后利用已知条件及相关结论，从不同方向和角度表示出目标向量(一般需建立两个不同的向量表达式)，再利用待定系数法确定系数，建立方程或方程组，解方程或方程组即得．
题型四：平面向量的坐标表示
【例4】（2024·全国·高一课堂例题）如图，是夹角为120°的两个单位向量，，且，．求在基下的坐标．

【解析】如图，
作平行四边形OBAC，则．
因为，，
所以，在中，，．
所以，即．
因此在基下的坐标为．
【变式4-1】（2024·全国·高一课堂例题）如图，设，，，P（x，y）是平面直角坐标系中的4个点，且，．求在基下的坐标．

【解析】，分别是x轴和y轴上的单位向量，并且相互垂直，因此不共线，则，组成平面上的一组基．
在轴上取与横坐标相同的点，则与轴平行或共线．
在轴上取与纵坐标相同的点，则与轴平行或共线．
因此．
由，的坐标可知，，
因此，即在基下的坐标为．
【变式4-2】（2024·高一课时练习）在直角坐标系中，向量、、的方向和长度如图所示，分别求它们的坐标．
【解析】根据题意，直角坐标系中，，，，
,,；
,,．
,,；
【方法技巧与总结】
在表示点、向量的坐标时，可利用向量的相等、加减法运算等求坐标，也可以利用向量、点的坐标定义求坐标．
题型五：平面向量加、减运算的坐标表示
【例5】（2024·全国·高一随堂练习）已知，，求，，的坐标．
【解析】由题意，，
，
.
【变式5-1】（2024·全国·高一随堂练习）已知，，求，的坐标．
【解析】因为，，则，
.
【变式5-2】（2024·全国·高一随堂练习）已知向量、的坐标，求、的坐标．
(1)，；
(2)，；
(3)，；
(4)，．
【解析】（1）因为，，则，
.
（2）因为，，则，
.
（3）因为，，则，
.
（4）因为，，则，
.
【变式5-3】（2024·新疆·高一校考期末），求，的坐标.
【解析】因为，
所以.
.
【方法技巧与总结】
平面向量坐标运算的技巧
（1）若已知向量的坐标，则直接应用两个向量和、差的运算法则进行．
（2）若已知有向线段两端点的坐标，则可先求出向量的坐标，然后再进行向量的坐标运算．
题型六：平面向量数乘运算的坐标表示
【例6】（2024·高一单元测试）已知点，()，试求当点在第三象限时，的取值范围 ．
【答案】
【解析】设，
∵，
∴，
∵，∴，
∴，解得，
∵点在第三象限，
∴，解得，
故答案为：.
【变式6-1】（2024·陕西宝鸡·高一统考期末）已知，，，若，则 .
【答案】
【解析】根据题意，由向量的坐标表示，列出方程，求出，，即可得出结果.因为，，，
若，则，解得，所以.
故答案为：.
【变式6-2】（2024·高一课时练习）已知点，，，，若，则的值为 ．
【答案】1
【解析】由题知，，，
由得，
∴∴
∴．
故答案为：1
【变式6-3】（2024·高一单元测试）已知,若,则的坐标是
【答案】
【解析】设，则， ，
，
，
，
∴的坐标是，
故答案为：．
【方法技巧与总结】
平面向量坐标运算的技巧
（1）若已知向量的坐标，则直接应用两个向量和、差及向量数乘的运算法则进行．
（2）若已知有向线段两端点的坐标，则可先求出向量的坐标，然后再进行向量的坐标运算．
（3）向量的线性坐标运算可完全类比数的运算进行．
题型七：向量共线的判定
【例7】（2024·广东佛山·高一佛山市三水区实验中学校考阶段练习）已知，，，则（ ）
A．，，三点共线B．，，三点共线
C．，，三点共线D．，，三点共线
【答案】D
【解析】由题意可得：，则有.
则A，C，D三点共线.
故选：D.
【变式7-1】（2024·全国·高一假期作业）已知向量不共线，，，，则（ ）
A．A，B，C三点共线B．A，C，D三点共线
C．A，B，D三点共线D．B，C，D三点共线
【答案】C
【解析】因为不共线，，，，
易得互不共线，所以A，B，C三点不共线，B，C，D三点不共线，故AD错误；
又，易得不共线，则A，C，D三点不共线，故B错误；
而，所以A，B，D三点共线，故C正确.
故选：C.
【变式7-2】（2024·江苏镇江·高一扬中市第二高级中学校考期末）设是平面内的一组基底，，则（ ）
A．三点共线B．三点共线
C．三点共线D．三点共线
【答案】C
【解析】A选项，设，则，无解，故三点不共线，A错误；
B选项，设，则，无解，故三点不共线，B错误；
C选项，，
，
故，故三点共线，C正确；
D选项，，
设，则，无解，故三点不共线，D错误.
故选：C
【方法技巧与总结】
向量共线的判定应充分利用向量共线定理或向量共线的坐标表示进行判断，特别是利用向量共线的坐标表示进行判断时，要注意坐标之间的搭配．
题型八：利用向量共线的坐标表示求参数
【例8】（2024·江苏泰州·高一校考期末）设，为平面内一个基底，已知向量，，，若A，B，D三点共线，则的值是（ ）
A． B． C． D．
【答案】D
【解析】因为，，
所以，
因为A，B，D三点共线，
所以有，即
因为，为平面内一个基底，
所以，不是共线向量，因此有，
故选：D
【变式8-1】（2024·河北邯郸·高一统考期末）已知向量，，，若B，C，D三点共线，则（ ）
A．－16B．16C．D．
【答案】A
【解析】由题意得，，
因为B，C，D三点共线，
所以，
则，得.
故选：A.
【变式8-2】（2024·新疆·高一八一中学校考期末）在平面直角坐标系中，向量，，，若A，B，C三点共线，则的值为（ ）
A．B．C．D．
【答案】C
【解析】因为A，B，C三点共线，
则，，
即，
则，解得.
故选：C
【方法技巧与总结】
利用向量平行的条件处理求值问题的思路
（1）利用向量共线定理列方程组求解．
（2）利用向量平行的坐标表达式直接求解．
提醒：当两向量中存在零向量时，无法利用坐标表示求值．
题型九：定比分点坐标公式及应用
【例9】（2024·高一课时练习）已知，，点P在线段AB的延长线上，且，则点P的坐标为 .
【答案】
【解析】点在线段的延长线上，且，
，
,,,．
所以点P的坐标为.
故答案为：.
【变式9-1】（2024·浙江宁波·高一宁波市北仑中学校考期末）已知两点，点在直线上，且满足，则点的坐标为 .
【答案】或/或；
【解析】若点在线段的反向延长线上，又因为，则有，设，则，所以，解得，即；
若点在线段上，又因为，则有设，则，所以，解得，即；
若点在线段的延长线上，又因为，则显然不成立；
故答案为:或.
【变式9-2】（2024·高一课时练习）已知，，若点分所成的比为，则 ， .
【答案】
【解析】因为点分所成的比为，所以，因为，，，所以，，所以
所以解得
故答案为：；
【方法技巧与总结】
用有向线段的定比分点坐标公式，可以求解有向线段的定比分点坐标及定点分有向线段所成的比．事实上用这个公式，还可巧妙地用于解决其它一些问题．如用得好，会使解题过程显得别具一格，简捷明快，充分展现我们思维的独创性．定比分点公式也是判定或证明两向量是否共线、平行的有效方法．
题型十：数量积的坐标运算
【例10】（2024·全国·高一假期作业）在平行四边形中，，，点为线段 的中点，则 .
【答案】
【解析】，以为原点，为轴，为轴，建立如图所示的平面直角坐标系，
，则，
有，，，，，
.
故答案为：
【变式10-1】（2024·新疆乌鲁木齐·高一乌鲁木齐市第四中学校考期末）已知向量，则 .
【答案】
【解析】，
，
，
故答案为：.
【变式10-2】（2024·全国·高一专题练习）如图，在矩形中，，，点为的中点，点在边上，若，则的值是 ．

【答案】2
【解析】建立如图所示的坐标系，
由图可得，，，，
，
即有．
即，，
则
．
故答案为：2．
【变式10-3】（2024·吉林长春·高一长春市第二十九中学校考阶段练习）设向量，，且，则m＝ ．
【答案】
【解析】因为，，所以，
又因为，所以，解得.
故答案为：
【方法技巧与总结】
进行数量积运算时，要正确使用公式，并能灵活运用以下几个关系．
题型十一：平面向量的模
【例11】（2024·全国·高一随堂练习）已知向量，非零向量与的夹角为，，则 .
【答案】
【解析】因为，所以，
又非零向量与的夹角为，，
所以，即，
所以，解得（舍去）或.
故答案为：
【变式11-1】（2024·安徽阜阳·高一校考阶段练习）设平面向量，，则 ．
【答案】
【解析】，
则.
故答案为：.
【变式11-2】（2024·河北石家庄·高一统考期末）已知，，且，则 ．
【答案】3
【解析】由已知得，
，
，
解得.
故答案为：3.
【变式11-3】（2024·上海虹口·高一上外附中校考期末）若，且，则的坐标为 ．
【答案】或
【解析】由，可设，则，
由，得，
解得，故或，
故答案为：或
【变式11-4】（2024·河南郑州·高一河南省实验中学校考期末）已知向量，，若，则 ．
【答案】
【解析】因为，
所以，解得，
则，，
所以，
所以，
故答案为：．
【方法技巧与总结】
求向量的模的常见思路及方法
（1）求模问题一般转化为求模的平方，即，求模时，勿忘记开方．
（2）或，此性质可用来求向量的模，可以实现实数运算与向量运算的相互转化．
题型十二：平面向量的夹角、垂直问题
【例12】（2024·河北邢台·高一统考期末）已知向量，，且，的夹角为钝角，则的取值范围为
【答案】
【解析】向量，，且，的夹角为钝角
且，不共线，
则,解得：且，
故答案为：.
【变式12-1】（2024·河北邯郸·高一统考期末）在平行四边形ABCD中，，，，，线段AE与BF相交于点G，则 .
【答案】
【解析】如图，不妨以A为原点，所在直线为横轴，建立直角坐标系，
过作轴于M点，由题意可得，，
则，，，，，
得，，
所以.
故答案为：.
【变式12-2】（2024·云南昆明·高一校考阶段练习）设x，，向量，，，且，，则向量与的夹角大小为 ．
【答案】
【解析】由题意得，解得，
故，，
则，
因为，所以.
故答案为：
【变式12-3】（2024·陕西榆林·高一校考期末）已知向量.
(1)求；
(2)设的夹角为，求的值；
(3)若向量与互相垂直，求的值.
【解析】（1）因为，所以；
（2）的夹角为，则；
（3）因为，所以，，
由向量与互相垂直得，，
所以，化简得，解得.
【变式12-4】（2024·四川遂宁·高一四川省蓬溪中学校校考阶段练习）已知向量
(1)当，且时，求
(2)当，，求向量与的夹角α的余弦值.
【解析】（1）向量
则，，
由，可得，
即，解得或，
又，所以，则，，
所以.
（2）由，则，
由，可得，解得，
所以，，，
.
【方法技巧与总结】
解决向量夹角问题的方法及注意事项
（1）求解方法：由直接求出．
（2）注意事项：利用三角函数值求的值时，应注意角的取值范围是．利用判断的值时，要注意时，有两种情况：一是是钝角，二是为；时，也有两种情况：一是是锐角，二是为．
题型十三：平面向量数量积的综合应用
【例13】（2024·全国·高一假期作业）在边长为的正方形中，是中点，则 ；若点在线段上运动，则的最小值是 .
【答案】
【解析】
根据题意，以为坐标原点，建立如图所示平面直角坐标系，
因为正方形的边长为，且是中点，
则，
则，
所以；
设，其中，
则，则，
所以，，
则，，
其中，，
当时，有最小值为.
所以的最小值是.
故答案为：30；
【变式13-1】（2024·全国·高一随堂练习）在等腰梯形ABCD中，已知，，，，动点E和F分别在线段BC和DC上，且，，则的最小值为 .
【答案】
【解析】由题意，，，
所以，，
又动点和分别在线段和上，且，，所以，解得，
，
当且仅当时，即时取等号，故的最小值为，
故答案为：．
【变式13-2】（2024·天津和平·高一统考期末）如图，在中，是线段上的点，且，是线段的中点，延长交于点，设，则 ；若为边长等于2的正三角形，则 .

【答案】 /-0.5
【解析】由于，则，
又是线段的中点，故
，
结合得，
故；
设，而，是线段的中点，
故
，
又三点共线，故，则，
故
，
又为边长等于2的正三角形，则
，
故答案为：；
【变式13-3】（2024·黑龙江牡丹江·高一牡丹江一中校考期末）在平行四边形中，，若点满足则 .
【答案】36
【解析】
由题意得，，所以.
故答案为：36.
【变式13-4】（2024·江西萍乡·高一统考期末）如图，在中，，，，动点在线段上移动，则的最小值为 ．

【答案】
【解析】在中，，，，
所以，又，
所以，
以所在直线为轴，以为原点，建立如图所示的直角坐标系，
则，，设，，
所以，
所以，
所以当时，有最小值.
故答案为：.
【方法技巧与总结】
坐标法
一、单选题
1．（2024·全国·高一随堂练习）已知向量，则（ ）
A．10B．5C．D．
【答案】C
【解析】因为，所以，所以.
故选：C
2．（2024·全国·高一假期作业）若，则实数（ ）
A．6B．C．3D．
【答案】B
【解析】因为，所以，
即，所以，
即，解得.
故选：B.
3．（2024·全国·高一假期作业）已知向量，，.若，且，则（ ）
A．B．C．D．
【答案】C
【解析】因为，，
由可得，，
即，整理得.
又因为，所以，
联立，解得或，
故，
故选C.
4．（2024·全国·高一随堂练习）已知向量，，若，则（ ）
A．B．
C．D．
【答案】A
【解析】法一：用坐标表示向量
由题意可知，，
由得，
，
整理得，，
所以．则A对；
法二：因为向量，
所以，
又，
所以，
所以.
故选：A．
5．（2024·全国·高一假期作业）在中，，是直线上的一点，若则实数的值为（ ）
A．B．C．D．
【答案】B
【解析】因为，所以，
又是直线上的一点，所以，
又，
所以，所以.
故选：B
6．（2024·全国·高一假期作业）已知平行四边形，若点是边的三等分点（靠近点处），点是边的中点，直线与相交于点，则（ ）
A．B．C．D．
【答案】C
【解析】
设，则，，
设，，
则，，
因为，
所以，解得，
所以，即.
故选：C.
7．（2024·全国·高一假期作业）已知平面向量，，若实数m，n满足，则与的夹角为（ ）
A．B．C．D．
【答案】B
【解析】因为，，所以，，
又，所以，
即，所以与的夹角为,
故选：B.
8．（2024·四川成都·高一四川省成都市第四十九中学校校考期末）已知是边长为1的正的边上的动点，为的中点，则的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】取AC的中点O，以O为原点，直线AC为x轴，建立如图所示的平面直角坐标系，
则：，设，
，
，且，
时，取最小值；时，取最大值，
∴的取值范围是，
故选：A.
二、多选题
9．（2024·全国·高一假期作业）已知，则（ ）
A．若，则
B．若，则
C．的最小值为2
D．若向量与向量的夹角为钝角，则的取值范围为
【答案】AB
【解析】已知，
若，则，解得，A选项正确；
若，则，解得，B选项正确；
，，
当时，有最小值，C选项错误；
当时，，，
向量与向量的夹角为，D选项错误.
故选：AB
10．（2024·浙江宁波·高一镇海中学校考期末）下列说法正确的是（ ）
A．已知，为平面内两个不共线的向量，则可作为平面的一组基底
B．，则存在唯一实数，使得
C．两个非零向量，，若，则与共线且反向
D．中，，，则为等边三角形
【答案】ACD
【解析】由，为平面内两个不共线的向量，
所以设，所以，则不存在，
所以与不共线，则可作为平面的一组基底，故A对；
只有当时，若，则存在唯一实数，使得，故B错；
因为两个非零向量，，设与夹角为，
由，平方得，
，所以，又，所以，则与共线且反向，
故C对；
在中，，所以，，所以，
由，得，即，则为等边三角形，故D对.
故选：ACD
11．（2024·全国·高一随堂练习）若平面向量，，其中，，则下列说法正确的是（ ）
A．若，则
B．若，则与同向的单位向量为
C．若，且与的夹角为锐角，则实数的取值范围为
D．若，则的最小值为
【答案】BD
【解析】由，，
A选项：，
则，解得，则，，
所以不存在，使，即，不共线，A选项错误；
B选项：，则，解得，
即，，，
所以与同向的单位向量为，B选项正确；
C选项：时，，
又与的夹角为锐角，
则，解得，且，
即，C选项错误；
D选项：由，得，即，
所以，
当且仅当，即时，等号成立，D选项正确；
故选：BD.
12．（2024·广东东莞·高一校考阶段练习）已知△ABC是边长为2的等边三角形，D，E分别是AC，AB上的点，且，，BD与CE交于点O，则下列说法正确的是（ ）
A．B．
C．D．在上的投影为
【答案】BCD
【解析】由题意知，为的中点，，
以为原点，分别为轴，轴正方向建立平面直角坐标系，
则，
设，则，
所以，解得，即为的中点，
所以，故B正确；
对于C：因为，故C正确；
对于A：因为，所以，故A错误；
对于D：因为，
在方向上的投影为，故D正确．
故选：BCD．
三、填空题
13．（2024·广东佛山·高一统考竞赛）已知中，分别为边上的点，且，.与的交点为，若，则 .
【答案】
【解析】由三点共线，得：，
又，
所以有，解得.
故答案为：.
14．（2024·新疆喀什·高一统考期末）已知中，D为的中点，，若，则 .
【答案】
【解析】因为,
所以,故;
故答案为：.
15．（2024·全国·高一随堂练习）在平行四边形 中， 点E满足且， 则实数 ．
【答案】4
【解析】由题意可得：
,
故答案为：4.
16．（2024·全国·高一随堂练习）已知，，则向量在上的投影向量的坐标为 ．
【答案】
【解析】因为，，
所以向量在上的投影向量为.
故答案为：.
四、解答题
17．（2024·陕西西安·高一阶段练习）如图所示，已知在△AOB中，BC=2AC，OD=2DB，DC和OA交于点E，设，．
(1)用和表示向量、；
(2)若，求实数λ的值
【解析】（1）由题意知，A是BC的中点，且，
由平行四边形法则，，
所以，
.
（2）因为，又，
，
所以＝，解得．
18．（2024·河南省直辖县级单位·高一济源市第四中学校考阶段练习）已知向量，，
(1)分别求，的坐标；
(2)若向量，且与向量平行，求实数k的值．
【解析】（1）依题意，，
.
（2）由（1）知，而，
由与向量平行，得，解得：，
所以实数k的值是.
19．（2024·全国·高一随堂练习）在中，已知在线段上，且，设．
(1)用向量表示；
(2)若，求．
【解析】（1）因为，所以，
由题得；
（2）由已知得，
．
20．（2024·辽宁大连·高一期末）在三角形中，，，，为线段上任意一点，交于.
(1)若.
①用表示.
②若，求的值.
(2)若，求的最小值.
【解析】（1）①因为，所以，
故在中，
；
②因为三点共线，设，
所以，
因为，
所以，
所以
又由①及已知，，
所以，解得.
（2）因为，又三点共线，设，
所以，
又因为，所以，
所以，，
当且仅当，即时取得等号，
所以的最小值为.
21．（2024·广西南宁·高一宾阳中学阶段练习）如图所示，在中，，，与相交于点，设，.
(1)试用向量表示；
(2)过点作直线分别交线段于点，记，，求证：不论点在线段上如何移动，为定值.
【解析】（1）因为三点共线，
所以存在实数使得，
又因为三点共线，
所以存在实数使得，
根据向量相等可得，解得，
所以.
（2）设，
由（1）可得①，②，
又三点共线，所以③，
由①②可得，，代入③式可得，
即不论点在线段上如何移动，为定值.
课程标准
学习目标
（1）能解释正交分解的含义，会举出正交分解的实例，能分析平面向量正交分解与平面向量基本定理的内在联系．
（2）能在平面向量坐标表示的基础上，得出平面向量的和、差、数乘运算的坐标表示，并进行相关的计算．
（3）能用坐标表示平面向量的数量积，会进行坐标表示下的平面向量数量积的运算；能描述两个平面向量夹角的含义，会用坐标表示向量的模与夹角．
（4）能用坐标表示向量共线的条件，并会用其判断两个向量是否共线；能用坐标表示向量垂直的条件，并会用其判断两个向量是否垂直；体会数形结合的思想．
（5）在探究平面向量基本定理和坐标表示的过程中，感悟联系的观点，体会转化与化归的思想，能说出用向量法解决几何问题的基本路径，体会用向量语言、向量方法表述和解决问题的简捷性．
（1）理解平面向量基本定理及其意义．
（2）会运用平面向量基本定理解决简单平面几何问题．
（3）借助平面直角坐标系，掌握平面向量的正交分解及坐标表示．
（4）会用坐标表示平面向量的加、减运算与数乘运算．
（5）能用坐标表示平面向量的数量积和两个平面向量的夹角．
（6）能用坐标表示平面向量共线、垂直的条件．
运算
坐标语言
加法与减法
记，
，
实数与向量的乘积
记，则