





初中数学北师大版(2024)八年级上册3 一次函数的图象多媒体教学课件ppt
展开1.(2022天津滨海新区期末)在平面直角坐标系中,下列各点 在函数y=2x-1的图象上的是( )A.(-2.5,-4) B.(3,1)C.(2.5,4) D.(-1,1)
解析 当x=2.5时,y=2x-1=4,所以点(2.5,4)在直线y=2x-1上,选 项C符合题意.其他选项点坐标均不符合函数y=2x-1,故选C.
2.一次函数y=4x+2的图象经过第 象限.( )A.一、二、三 B.一、二、四C.一、三、四 D.二、三、四
解析 ∵一次函数y=4x+2中,k=4>0,b=2>0,∴函数图象经过第一、二、三象限.故选A.
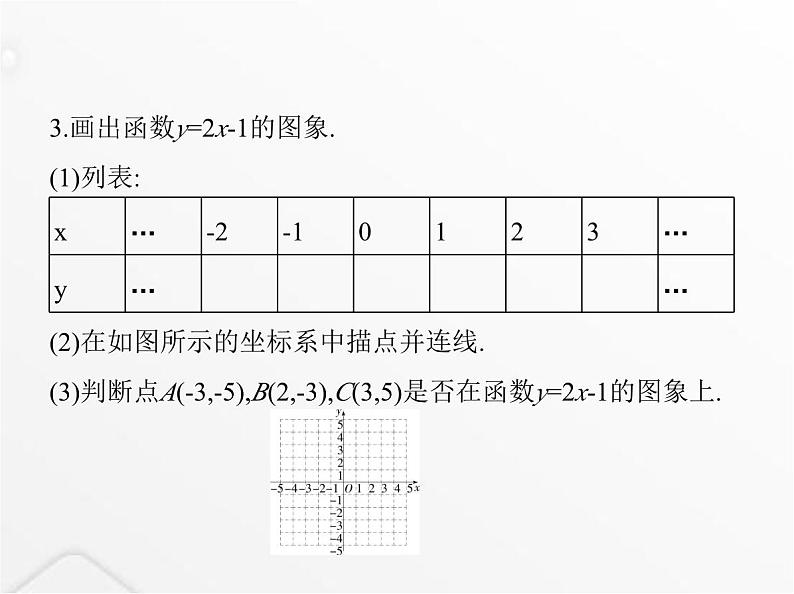
3.画出函数y=2x-1的图象.(1)列表:
(2)在如图所示的坐标系中描点并连线.(3)判断点A(-3,-5),B(2,-3),C(3,5)是否在函数y=2x-1的图象上.
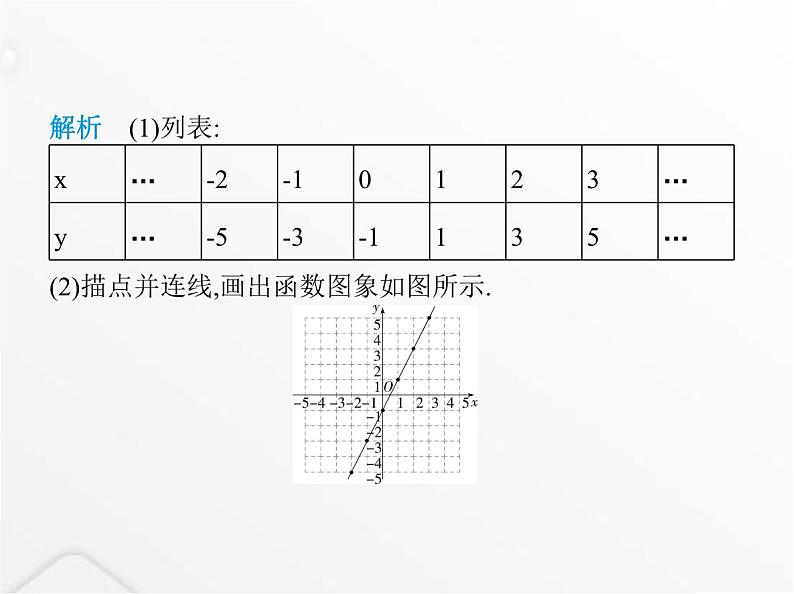
解析 (1)列表:(2)描点并连线,画出函数图象如图所示.
(3)把x=-3代入y=2x-1,得y=-7≠-5,把x=2代入y=2x-1,得y=3≠-3,把x=3代入y=2x-1,得y=5,所以点C在函数y=2x-1的图象上,点A和B不在函数y=2x-1的图象上.
4.(2024安徽六安期末)下列函数中,y随x的增大而减小的是 ( )A.y=5x+3 B.y=2x-4C.y=-3x+4 D.y=x+3
解析 当k<0时,y随x的增大而减小,故选C.
5.(一题多解)(2024江苏淮安期末)已知点(-2,y1),(3,y2)都在直 线y=-2x+1上,则y1与y2的大小关系为 ( )A.y1>y2 B.y1=y2C.y1
6.(2023辽宁沈阳中考)已知一次函数y=kx+b的图象如图所示, 则k,b的取值范围是 ( )A.k>0,b>0 B.k>0,b<0C.k<0,b>0 D.k<0,b<0
解析 由题图可知该一次函数图象经过第一、三、四象限, 则k>0,b<0.故选B.
7.关于一次函数y=-4x-8的说法中,正确的是 ( )A.该函数图象不经过第三象限B.该函数图象经过点(2,0)C.y随x的增大而增大D.该函数图象与坐标轴围成的三角形面积为8
解析 A.一次函数y=-4x-8中,k=-4<0,b=-8<0,所以函数图象 经过第二、三、四象限,不经过第一象限,故该选项错误;B.直线y=-4x-8,令y=0,得-4x-8=0,解得x=-2,所以函数图象经过点(-2,0),故该选项错误;C.由于k=-4<0,所以y随x的增大而减小,故该选项错误;D.直线y=-4x-8,令x=0可得y=-8,因此该函数图象与y轴的交点 坐标为(0,-8),又该函数图象与x轴的交点坐标为(-2,0),∴函数 图象与坐标轴围成的三角形面积为 ×2×8=8,故该选项正确.故选D..
8.(易错题)(2023四川成都模拟)已知一次函数y=mx+n的图象 不经过第二象限,则m,n的取值范围为 .
解析 ∵一次函数y=mx+n的图象不经过第二象限,∴m>0.当此函数图象经过原点时,n=0;当此函数图象不经过原点时,n<0.故答案为m>0,n≤0.
9.(2024安徽六安期末)函数y=-x+b的图象与x轴、y轴分别交 于点A、B,△AOB的面积为8,则b的值为 .
10.已知函数y=(2m+1)x+m-3.(1)若函数图象经过原点,求m的值.(2)若函数的图象平行于直线y=3x-3,求m的值.(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取 值范围.
解析 (1)∵函数y=(2m+1)x+m-3的图象经过原点,∴当x=0时,y=0,即2m+1≠0,m-3=0,解得m=3.(2)∵函数y=(2m+1)x+m-3的图象与直线y=3x-3平行,∴2m+1= 3,解得m=1.(3)∵函数y=(2m+1)x+m-3是一次函数,且y随x的增大而减小, ∴2m+1<0,∴m<- .
11.(新独家原创)已知|m+2|+ =0,函数y=mx+n的图象与x轴、y轴分别交于点A、B.(1)求A、B的坐标,并在如图所示的直角坐标系中画出它的 图象.(2)从图象看,x取何值时,y>0?(3)直线AB上是否存在一点C(C与B不重合),使△BOC的面积 等于6?若存在,求出点C的坐标;若不存在,请说明理由.
解析 (1)∵|m+2|+ =0,∴m+2=0,n-3=0,解得m=-2,n=3,∴函数的解析式为y=-2x+3.由y=0,得x= ,由x=0,得y=3,∴A ,B(0,3).函数图象如图所示:
12.(2023甘肃兰州中考,11,★★☆)一次函数y=kx-1的函数值y 随x的增大而减小,当x=2时,y的值可以是 ( )A.2 B.1 C.-1 D.-2
解析 ∵一次函数y=kx-1的函数值y随x的增大而减小,∴k<0,∴当x=2时,y=2k-1<-1.故选D.
13.(2023陕西中考A卷,5,★★☆)在同一平面直角坐标系中, 函数y=ax(a≠0)和y=x+a的图象可能是 ( )
解析 A.由函数y=ax(a≠0)图象得a>0,与y=x+a图象的a<0矛 盾,故本选项不符合题意;B.函数y=x+a的图象所过象限错误,故本选项不符合题意;C.函数y=x+a的图象所过象限错误,故本选项不符合题意;D.由函数y=ax(a≠0)图象得a<0,与y=x+a图象的a<0一致,故 本选项符合题意.故选D.
思想解读 数形结合主要是指数与形之间的一一对应关系, 数形结合就是将直观的几何位置、图形关系与抽象的数量 关系、数学语言相结合,通过“以数解形”“以形助数”使 抽象问题具体化、复杂问题简单化.
14.(新考法)(2022浙江绍兴中考,9,★★☆)已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1
解析 ∵直线y=-2x+3中,-2<0,∴y随x的增大而减小,当y=0时,x=1.5,∵(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1
若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2> 0,故选项D符合题意.故选D.
15.(2024福建漳州长泰一中期中,10,★★☆)已知一次函数y= kx+k-1的图象过点A(a,a),则下列说法不正确的是 ( )A.当k=1时,y=kx+k-1一定为正比例函数B.当a=0时,y=kx+k-1一定为正比例函数C.当k<0时,a的值一定为-1D.当a<0时,y的值一定随x值的增大而减小
解析 选项A,把k=1代入y=kx+k-1,则y=x,是正比例函数,故该 选项说法正确.选项B,当a=0时,A(0,0),把A(0,0)代入y=kx+k-1,则k=1,则y=x,是 正比例函数,故该选项说法正确.选项C,把A(a,a)代入y=kx+k-1,得a=ak+k-1,∵k<0,∴a= =-1,故该选项说法正确.选项D,把A(a,a)代入y=kx+k-1,得a=ak+k-1,当k≠1时,有a= =-1<0,k的值不一定为负数,故y的值不一定随x值的增大而减小,故该选项说法错误.故选D.
16.(2024广东深圳实验学校期中,14,★★☆)已知关于x的一 次函数y=mx+n的图象如图所示,则|n-m|- 可化简为 .
17.(2024四川成都七中育才学校期中,17,★★☆)如图,在平 面直角坐标系xOy中,直线l1:y=- x+ 与x轴交于点A,直线l2:y=2x+b与x轴交于点B,且与直线l1交于点C(-1,m).(1)求m和b的值.(2)求△ABC的面积.(3)若将直线l2向下平移t(t>0)个单位长度后,所得到的直线与 直线l1的交点在第一象限,直接写出t的取值范围.
解析 (1)把C(-1,m)代入l1:y=- x+ ,得m=- ×(-1)+ =2,把C(-1,2)代入l2:y=2x+b,得2=-2+b,∴b=4.(2)当- x+ =0时,x=2,∴A(2,0).当2x+4=0时,x=-2,∴B(-2,0).∴AB=4,
∴△ABC的面积= AB·yC= ×4×2=4.(3)
解析 (1)令x=0,得y=2×0+4=4,∴B(0,4),∴OB=4,∵点C是OB的中点,∴OC=BC=2,∴C(0,2).(2)令y=0,有0=2x+4,解得x=-2.∴A(-2,0),∴OA=2,∴S△ABC= ×BC×OA= ×2×2=2.设点D(m,0),则AD=|m+2|,
∵S△ABC=S△ACD,∴ ×AD×OC= ×|m+2|×2=2,解得m=-4或m=0,∴点D的坐标为(-4,0)或(0,0).(3)假设存在,设点P的坐标为(n,0),∵∠BAP确定,∴△ABP是直角三角形需分两种情况分析:①当∠APB=90°时,点P与原点O重合,坐标为(0,0).②当∠ABP=90°时,AB2+BP2=AP2,∵OA=2,OB=4,OP=|n|=n,AP=n+2,
初中数学北师大版八年级上册第四章 一次函数3 一次函数的图象评课课件ppt: 这是一份初中数学北师大版八年级上册第四章 一次函数3 一次函数的图象评课课件ppt,共13页。PPT课件主要包含了情景导入,思考探究获取新知,解列表,y-2x+1,你发现什么,做一做,y2x+3,y-x,y-x+3,y5x-2等内容,欢迎下载使用。
北师大版八年级上册3 一次函数的图象作业ppt课件: 这是一份北师大版八年级上册3 一次函数的图象作业ppt课件,共22页。
初中数学3 一次函数的图象教学演示ppt课件: 这是一份初中数学3 一次函数的图象教学演示ppt课件,共13页。PPT课件主要包含了情景导入,思考探究获取新知,解列表,y-2x+1,你发现什么,做一做,y2x+3,y-x,y-x+3,y5x-2等内容,欢迎下载使用。













