北师大版八年级上册3 一次函数的图象教学ppt课件

这是一份北师大版八年级上册3 一次函数的图象教学ppt课件，共22页。PPT课件主要包含了函数图象概念，ykxk≠0，相关知识，-2-4，-1-2，正比例函数图象，正比例函数的性质，经过原点的直线，k0k0，三象限等内容，欢迎下载使用。

1. 能根据正比例函数的图象和表达式 y =kx（k≠0）理解k＞0和k＜0时，函数的图象特征与增减性。2. 掌握正比例函数的性质，并能灵活运用解答有关问题。
4.3 一次函数的图象第1课时 正比例函数的图象
2. 一次函数的解析式：
y=kx+b(k≠0)
3. 正比例函数的解析式：
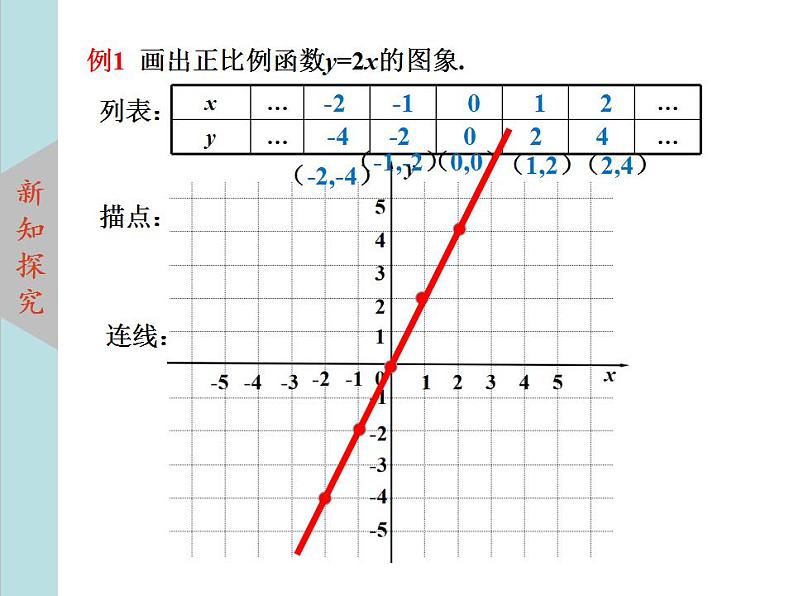
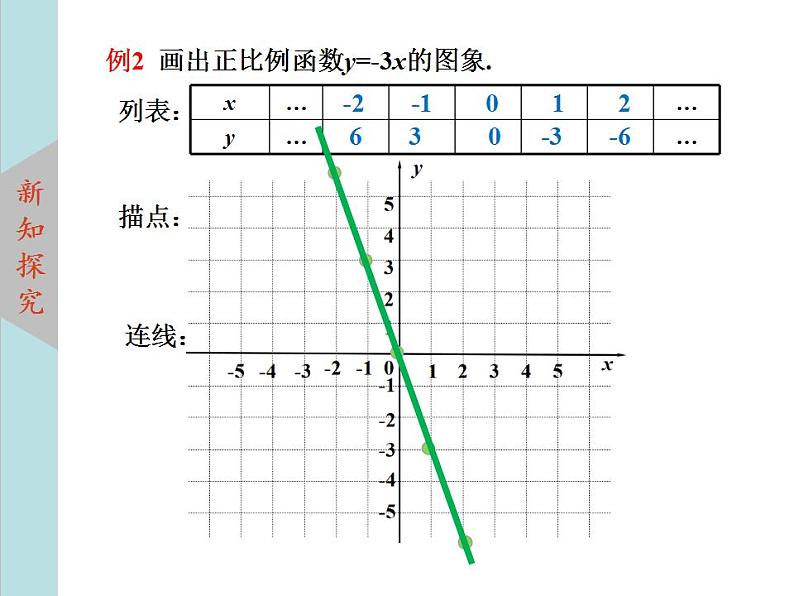
(1)函数图象：把一个函数自变量的每一个值与对应的函数值分别作为点的横坐标和纵坐标，在直角坐标系内描出相应的点，所有这些点组成的图形叫做该函数的图象．(2) 函数图象的画法步骤： （1）列表； （2）描点； （3）连线.
例1 画出正比例函数y=2x的图象.
-2 -1 0 1 2
-4 -2 0 2 4
例2 画出正比例函数y=-3x的图象.
6 3 0 -3 -6
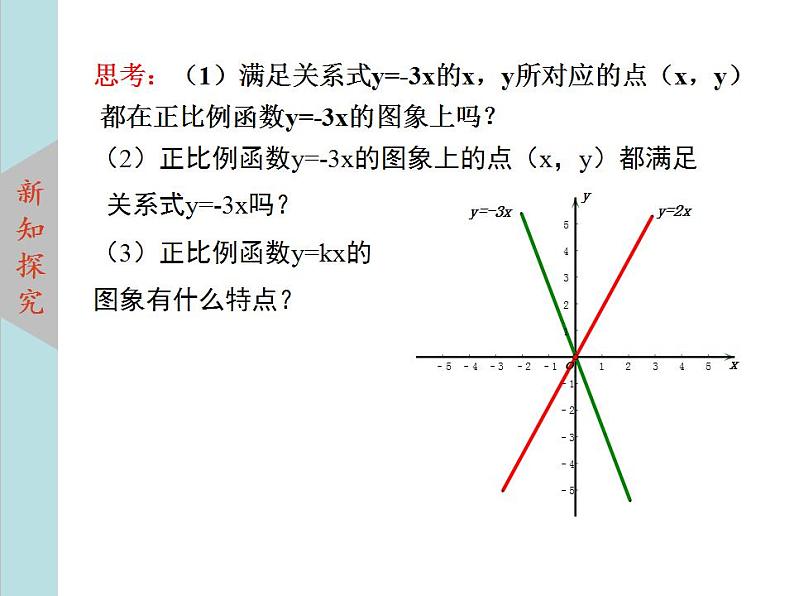
思考：（1）满足关系式y=-3x的x，y所对应的点（x，y） 都在正比例函数y=-3x的图象上吗？（2）正比例函数y=-3x的图象上的点（x，y）都满足 关系式y=-3x吗？（3）正比例函数y=kx的图象有什么特点？
正比例函数y=kx的图象是一条经过原点（0,0）的直线.
画正比例函数图象时，只要再确定一个点，过这点和原点画直线就可以了.
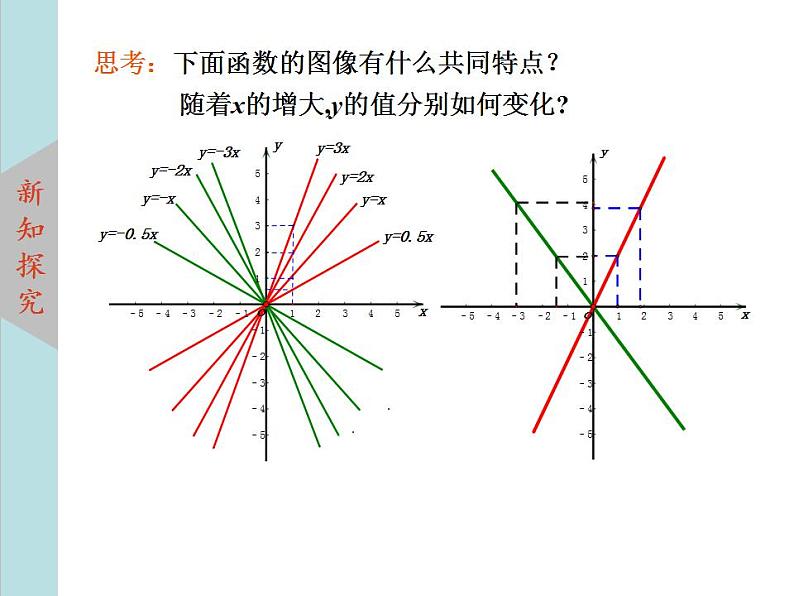
思考：下面函数的图像有什么共同特点？ 随着x的增大,y的值分别如何变化?
|k|越大，直线越陡，直线越靠近y轴.
例 已知正比例函数y=mx的图象经过点（m，4），且y的值随着x值的增大而减小，求m的值.
解: 因为正比例函数y=mx的图象经过点（m，4）,所以4=m·m，解得m=±2. 又因为y的值随着x值的增大而减小， 所以m<0，故m=－2.
1. 正比例函数y= x的图象大致是(　　)
2. 正比例函数y=kx的图象如图所示,则k的值为 (　　)
3. 已知正比例函数y=(m-3)x的图象经过第二、四象限,则m的取值范围是 (　　)A.m≥3B.m>3C.m≤3D.m<3
4. 若函数y=(m+1)x|m|是正比例函数,则该函数的图象经过第　　　　象限. 
4. 若正比例函数的图象经过点(-1,2)和(m,3),则m的值为　　　　. 
5. 若点A(-5,y1)和点B(-6,y2)都在函数y=-9x的图象上,则y1与y2的大小关系是 (　　)A.y1y2C.y1=y2D.无法确定
6. 已知正比例函数y=kx(k是常数, k≠0)的图象经过第二、四象限,那么y的值随着x值的增大而　　　 . (填“增大”或“减小”) 
7. 对于函数 下列说法不正确的是(　　)A．其图象经过点(0，0)B．其图象经过点C．其图象经过第二、四象限D．y随x的增大而增大
8. 在正比例函数y＝－3mx的图象中，函数y的值随x值的增大而增大，则P(m，5)在(　　)A．第一象限 B．第二象限C．第三象限 D．第四象限
9. 函数y＝3x，y＝－2x， 的共同特点是(　　)A．图象位于同样的象限 B．y随x增大而减小C．都经过原点 D．y随x增大而增大
正比例函数的图象和性质
图象：经过原点的直线.当k>0时，经过第一、三象限；当k<0时，经过第二、四象限.
性质：当k>0时，y的值随x值的增大而增大；当k<0时，y的值随x值的增大而减小.
画正比例函数图象的一般步骤：列表、描点、连线