苏科版九年级下册5.4 二次函数与一元二次方程课前预习ppt课件

这是一份苏科版九年级下册5.4 二次函数与一元二次方程课前预习ppt课件，共33页。PPT课件主要包含了教学目标，-1或4，x-1或x4，没有交点→没有实数根，有两个不同的实数根，没有实数根等内容，欢迎下载使用。

理解二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0的关系，能根据二次函数y=ax2+bx+c的图像确定一元二次方程ax2+bx+c=0的根的情况
掌握直线与抛物线的交点问题——会求直线与抛物线的交点坐标，并会判断直线与抛物线的交点个数
图像法确定一元二次方程的根的情况
Q1：二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0有怎样的关系？
令y=0，得：ax2+bx+c=0当二次函数y=ax2+bx+c的y=0时，有一元二次方程ax2+bx+c=0
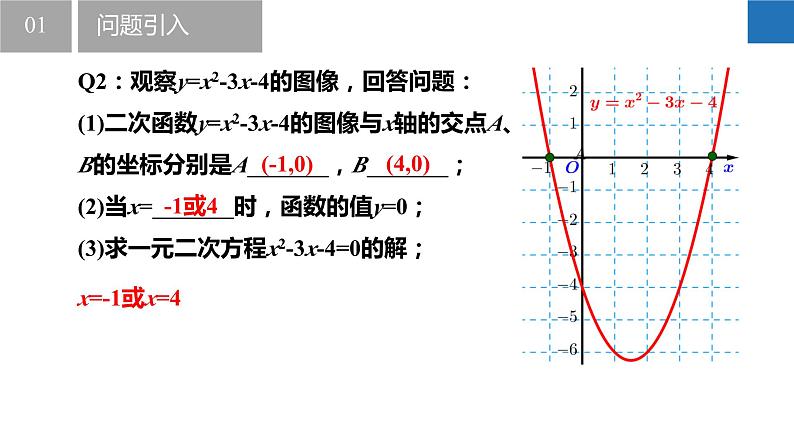
Q2：观察y=x2-3x-4的图像，回答问题：(1)二次函数y=x2-3x-4的图像与x轴的交点A、B的坐标分别是A_______，B_______；(2)当x=_______时，函数的值y=0；(3)求一元二次方程x2-3x-4=0的解；
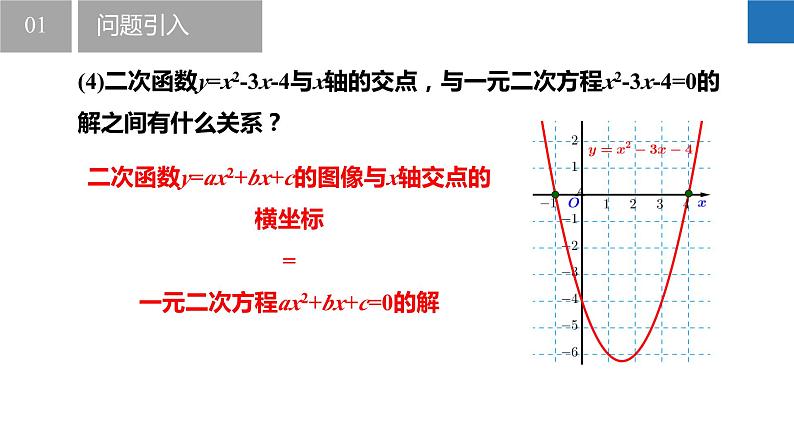
(4)二次函数y=x2-3x-4与x轴的交点，与一元二次方程x2-3x-4=0的解之间有什么关系？
二次函数y=ax2+bx+c的图像与x轴交点的横坐标=一元二次方程ax2+bx+c=0的解
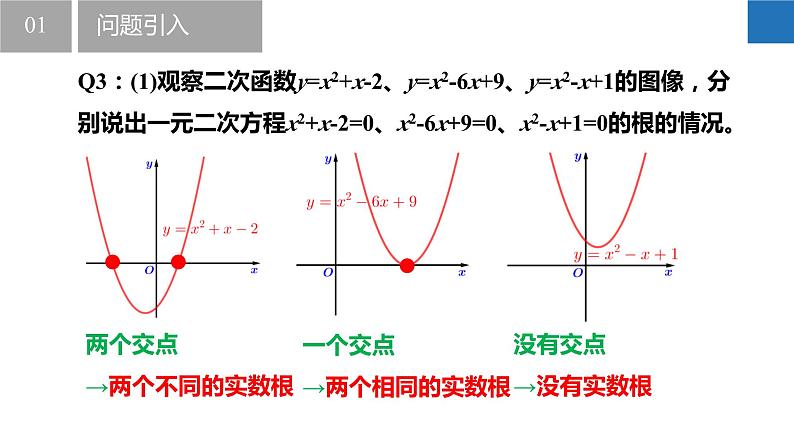
Q3：(1)观察二次函数y=x2+x-2、y=x2-6x+9、y=x2-x+1的图像，分别说出一元二次方程x2+x-2=0、x2-6x+9=0、x2-x+1=0的根的情况。
两个交点→两个不同的实数根
一个交点→两个相同的实数根
(2)利用判别式法检验(1)中结论是否正确。
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
ax2+bx+c=0(a≠0)有两个不同的实数根
ax2+bx+c=0(a≠0)有两个相同的实数根
ax2+bx+c=0(a≠0)没有实数根
y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解
例1、求二次函数y=(x-5)(x-7)的图像与x轴的交点坐标。
解：令y=0，即(x-5)(x-7)=0，解得：x=5或x=7，∴二次函数y=(x-5)(x-7)的图像与x轴的交点坐标为(5,0)和(7,0)。
例2、二次函数y=x2-6x+n的部分图像如图所示，若关于x的一元二次方程x²-6x+n=0的一个解x1=1，求另一个解x2。
解：∵二次函数的图像与x轴的一个交点为(1,0)，且对称轴为x=3，∴另一个交点为(5，0)，∵y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解，∴x²-6x+n=0的另一个解x2=5。
例3、(1)求抛物线y=kx2+(2k+1)x+2的图像与x轴的两个交点；(2)若(1)中两个交点的横坐标均为整数，且k为正整数，试求出该二次函数的表达式；(3)已知抛物线y=kx2+(2k+1)x+2恒过定点，直接写出定点的坐标。
例3、(1)求抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点；(2)若(1)中两个交点的横坐标均为整数，且k为正整数，试求出该二次函数的表达式；(3)已知抛物线y=kx2+(2k+1)x+2恒过定点，直接写出定点的坐标。
例4、抛物线y=ax2-2x+3与x轴有两个交点，求a的取值范围。
例5、已知抛物线y=4x2+2x+c，且当-1例6、已知关于x的一元二次方程：x2-(m-3)x-m=0(1)试判断原方程根的情况；(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0)，B(x2,0)两点，则A，B两点间的距离是否存在最大或最小值？若存在，求出这个值；若不存在，请说明理由。（友情提示：AB=|x1-x2|）
直线与抛物线的交点问题
Q1：求直线y=1与抛物线y=x2-3x+3的交点坐标
直线与抛物线联立，化简可得一元二次方程
Q2：求直线y=x+1与抛物线y=x2-4x+7的交点坐标
（一）求直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点坐标：
（二）判断直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点个数：
例1、抛物线与直线y=m有交点，图中抛物线的表达式为y=ax²+bx+c，根据图像判断下列方程根的情况。（1）方程ax²+bx+c=0的两根分别为__________________;（2）方程ax²+bx+c-3=0的两根分别为__________________;（3）方程ax²+bx+c=2的根的情况是__________________;（4）方程ax²+bx+c=4的根的情况是__________________。
可以看作：抛物线y=ax²+bx+c与直线y=3联立所得，故方程的两根=抛物线y=ax²+bx+c与直线y=3交点的横坐标。
x1=-1，x2=-1
可以看作：抛物线y=ax²+bx+c与直线y=2联立所得，故方程的根的情况需分析抛物线y=ax²+bx+c与直线y=2的交点情况。
可以看作：抛物线y=ax²+bx+c与直线y=4联立所得，故方程的根的情况需分析抛物线y=ax²+bx+c与直线y=4的交点情况。
例2、(1)求直线y=x+1与抛物线y=x2-1的交点坐标；(2)求直线y=2x-6与抛物线y=2x²-6x+4的交点坐标。
例3、已知a，b是关于x的方程(x-a)(x-b)=2的两个根，其中a可以看作：抛物线y=(x-a)(x-b)与直线y=2联立所得
图像法确定一元二次方程的根的情况:
直线与抛物线的交点问题：