初中数学苏科版九年级下册5.4 二次函数与一元二次方程说课课件ppt

这是一份初中数学苏科版九年级下册5.4 二次函数与一元二次方程说课课件ppt，共15页。PPT课件主要包含了方程x2+2x0，b2-4ac0，x-2，没有实数根等内容，欢迎下载使用。

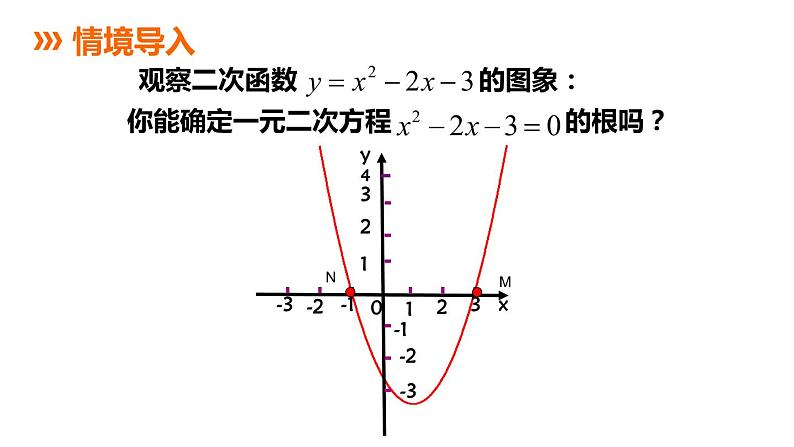
观察二次函数 的图象：
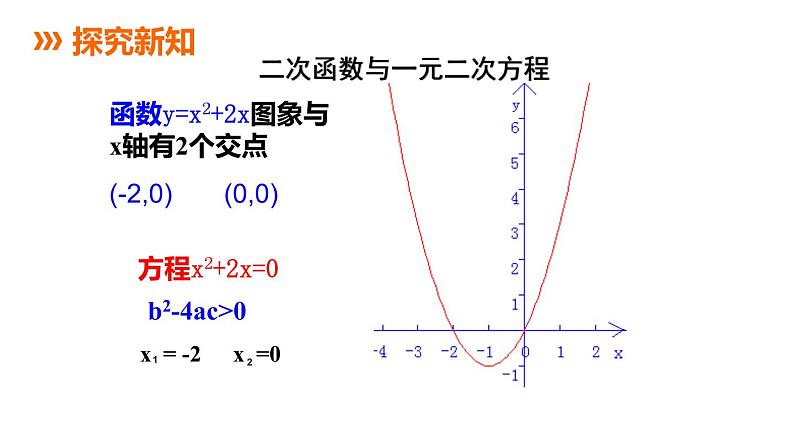
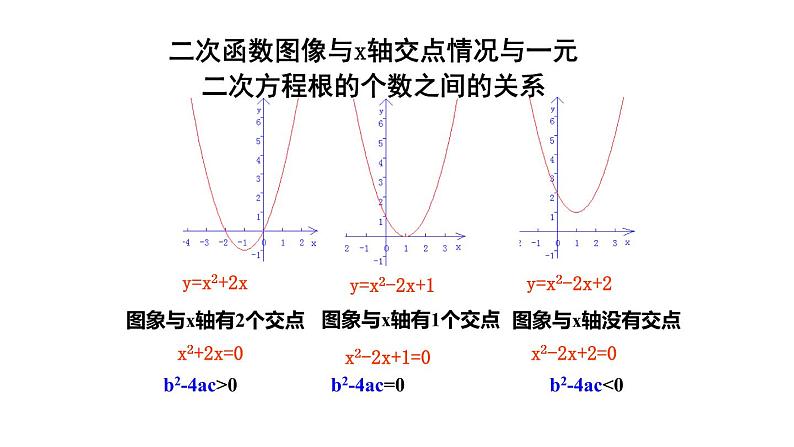
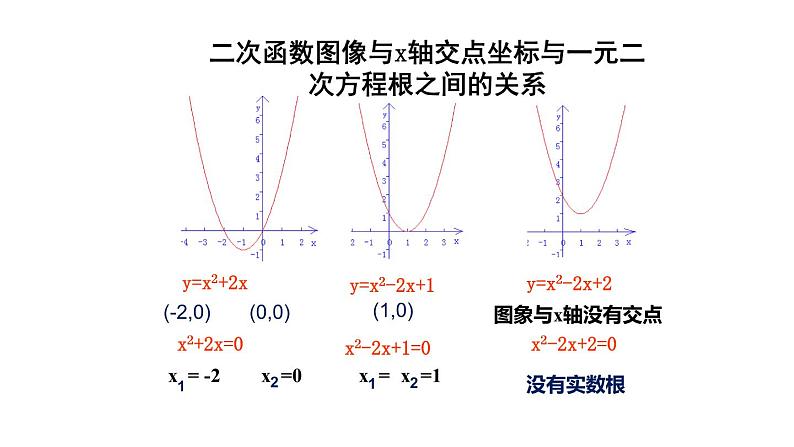
函数y=x2+2x图象与x轴有2个交点(-2,0) (0,0)
二次函数与一元二次方程
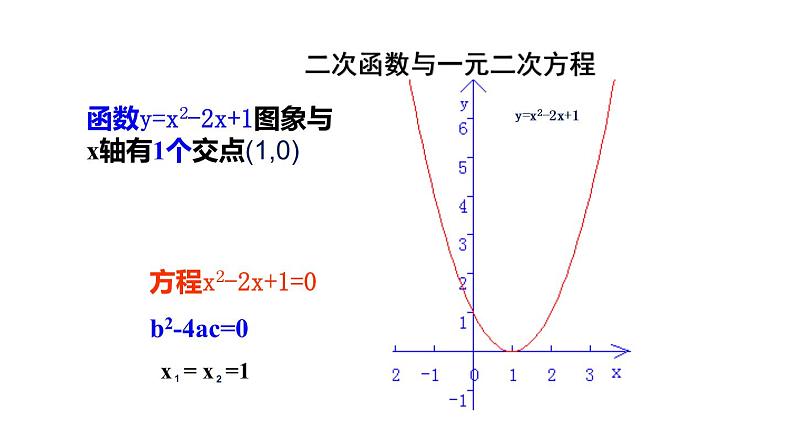
函数y=x2-2x+1图象与x轴有1个交点(1,0)
方程x2-2x+1=0
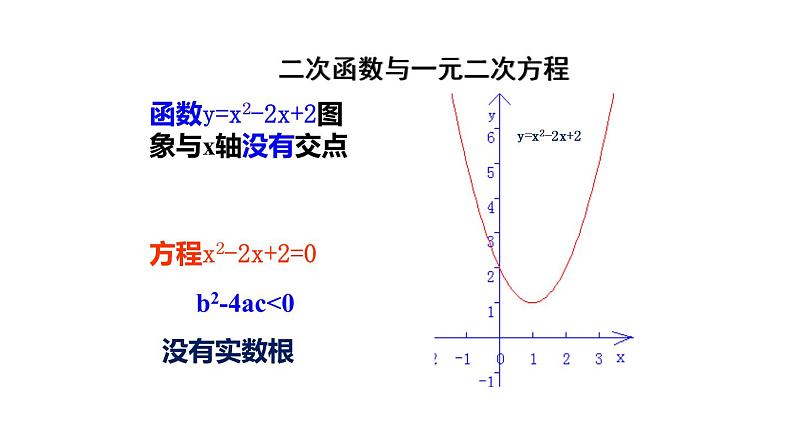
函数y=x2-2x+2图象与x轴没有交点
方程x2-2x+2=0
二次函数图像与x轴交点情况与一元二次方程根的个数之间的关系
(-2,0) (0,0)
二次函数图像与x轴交点坐标与一元二次方程根之间的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:①有两个交点,②有一个交点,③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
抛物线y=ax2+bx+c与x轴有两个交点
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明：
1、b2-4ac＞0 一元二次方程ax2+bx+c=0有两个不等的实数根
抛物线y=ax2+bx+c与x轴有唯一公共点
2、b2-4ac=0 一元二次方程ax2+bx+c=0有两个相等的实数根
抛物线y=ax2+bx+c与x轴没有公共点
3、b2-4ac＜0 一元二次方程ax2+bx+c=0没有实数根
例1求二次函数图象y=x2-3x+2与x轴的交点的坐标。
解：∵交点在x轴上， ∴它们的纵坐标为0， ∴令y=0，则x2-3x+2=0 解得：x1=1，x2=2； ∴（1，0） ， （2，0）
例2不画图象，判断二次函数y=-x2+5x-8的图像与x轴是否有公共点。
解：因为一元二次方程-x2+5x-8=0的根的判别式b2-4ac=52-4×（-1）×（-8）＜0，所以方程-x2+5x-8=0没有实数根。二次函数y=-x2+5x-8的图像与x轴没有公共点.
例3 [教材补充例题] 已知抛物线y=x2+4kx+4k2-3k.(1)当k为何值时,抛物线与x轴有两个交点?(2)当k为何值时,抛物线与x轴无交点?
[解析] 根据二次函数与一元二次方程的关系,将抛物线与x轴的交点问题转化为一元二次方程根的判别式问题,列出不等式解答.
解:(1)∵ 抛物线与x轴有两个交点,∴b2-4ac>0,∴(4k)2-4×(4k2-3k)>0,解得k>0.故当k>0时,抛物线与x轴有两个交点.(2)∵ 抛物线与x轴无交点,∴b2-4ac<0,∴(4k)2-4×(4k2-3k)<0,解得k<0.故当k<0时,抛物线与x轴无交点.
1、方程 的根是 ；则函数 的图象与x轴的交点有 个，其坐标是 ．
（-5，0）、（1，0）
2、方程 的根是 ____ ；则函数 的图象与x轴的交点有_____ 个，其坐标是 ．
3、下列函数的图象中，与x轴没有公共点的是（ ）