北师大版数学七年级下册 4.3.2 《探索三角形全等的条件》第2课时 课件+分层练习（含答案解析）

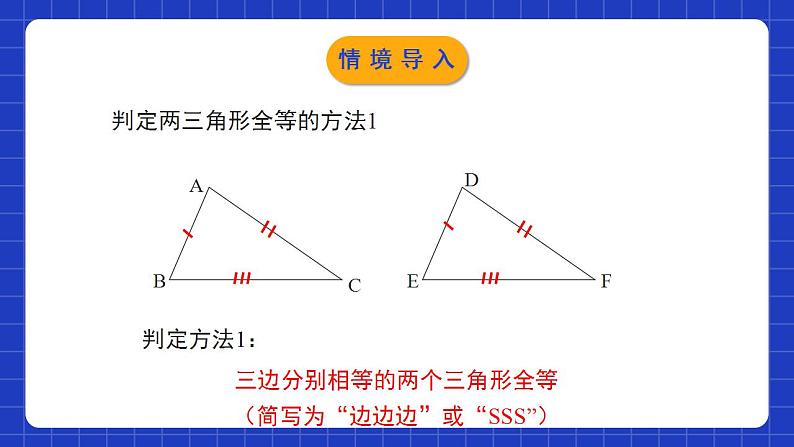
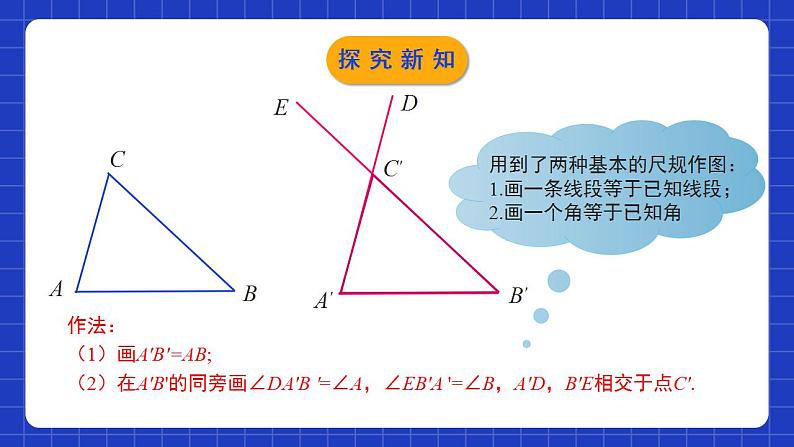
4.3.2探索三角形全等的条件第2课时学习目标1探索并正确理解三角形全等的判定方法“ASA”和“AAS”．2会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.判定两三角形全等的方法1ABCDEF三边分别相等的两个三角形全等（简写为“边边边”或“SSS”）判定方法1：情境导入 一张教学用的三角形硬纸板不小心被撕坏了，如图，你能制作一张与原来同样大小的新教具？能恢复三角形的原貌吗？情境导入三角形全等的判定（“角边角”） 思考：我们知道:如果给出一个三角形三条边的长度,那么因此得到的三角形都是全等.如果已知一个三角形的两角及一边,那么有几种可能的情况呢?1.角.边.角;2.角.角.边.每种情况下得到的三角形都全等吗?探究新知 如果“两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60°和80°，它们所夹的边为2cm，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？2cm全等探究新知 先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ，使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下，放到△ABC上，它们全等吗？探究新知作法：（1）画A'B'=AB;（2）在A'B'的同旁画∠DA'B '=∠A，∠EB'A '=∠B，A'D，B'E相交于点C'.A′B′C′ED探究新知归纳总结 两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或“ASA”。符号语言： ∵在△ABC和△DEF中 ∠B=∠E （已知） BC=EF （已知） ∠C= ∠F （已知） ∴ △ABC ≌△DEF （ASA） 三角形全等的判定2 探究新知 如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗?答：带1去，因为有两角且夹边分别相等的两个三角形全等.探究新知用“角角边”判定三角形全等 若三角形的两个内角分别是∠A=70°和∠B=45°，且∠B所对的边为5cm，你能画出这个三角形吗?画出的三角形与伙伴们全等吗？ABC70°45°5cm探究新知你和其他同学画的三角形全等吗？若改变角度和边长，你能得到同样的结论吗？转化的思想：角角边 角边角 由三角形内角和定理可知，两角相等，则必然三角都相等！探究新知两角和其中一角的对边对应相等的两个三角形全等。简写成“角角边”或“AAS”。符号语言： ∵在△ABC和△DEF中 ∠B=∠E （已知） ∠C= ∠F （已知） AC = DF （已知） ∴ △ABC ≌△DEF （AAS） 三角形全等的判定3 归纳总结探究新知1、相同点：都已知两个角和一条边2、不同点：“ASA”在已知的两个三角形中的顺序是：“AAS”在已知的两个三角形中的顺序是：两角及夹边两角及其中一角的对边比较“ASA”和“AAS”判定方法的异同点：归纳总结探究新知例：如图，AD∥BC，BE∥DF，AD＝CB，试说 明：△ADF≌△CBE. 解：∵AD∥BC，BE∥DF， ∴∠A＝∠C， ∠DFE＝∠BEC. 在△ADF和△CBE中，∠A=∠C ∠DFE＝∠BECAD＝BC∴△ADF≌△CBE(AAS).探究新知1．下列结论中，正确的是（ 　 ）A．有两条边对应相等的两个三角形全等B．有一个角和两条边对应相等的两个三角形全等C．有两个角和它们的夹边对应相等的两个三角形全等D．任意两个直角三角形全等C随堂练习2.已知△ABC和△A1B1C1中，∠A＝∠A1， AB＝A1B1， 再补充下列哪个条件可以根据“ASA”判断△ABC和△A1B1C1全等（ ）A．∠B＝∠B1　　　　B．∠C＝∠C1 C．AC＝A1C1　　　　 D．以上均不对A随堂练习3．在△ABC和△DEF中，若∠A＝∠D，∠B＝∠E，BC＝EF，则△ABC≌△DEF，根据是_______．AAS4.如图，Rt△ABC中，∠BAC＝90°，AB＝AC，分别过点B，C作过点A的直线的垂线BD，CE，垂足分别为D，E，若BD＝3，CE＝2，则DE＝ ．5随堂练习5．解决课前导入的问题：一张教学用的三角形硬纸板不小心被撕坏了，如下图，你能制作一张与原来同样大小的新教具吗？能恢复原来三角形的原貌吗？随堂练习被撕坏的这块三角形硬纸板保留了原三角形硬纸板的两角及其夹边，新制作的三角形硬纸板的两角及其夹边和被撕坏的这块三角形硬纸板对应相等，新制作的三角形硬纸板和原三角形硬纸板满足“角边角”，自然就同样大小了，所以能恢复原来三角形的原貌．随堂练习6.如图，在△ABC中，AD⊥BC于点D，BE⊥AC于E．AD与BE交于F，若BF＝AC，试说明：△ADC≌△BDF．分析：先说明∠ADC＝∠BDF，∠DAC＝∠DBF，再由BF＝AC，根据“AAS”即可得出两三角形全等．BACDEF随堂练习∵∠AFE＝∠BFD，　∠DAC＋∠AEF＋∠AFE＝180°，　∠BDF＋∠BFD＋∠DBF＝180°解：∵AD⊥BC，∴∠ADC＝∠BDF＝∠BEA＝90°．∴∠DAC＝∠DBF．在△ADC和△BDF中，∵AC＝BF,∴△ADC≌△BDF(AAS)．BACDEFBE⊥AC，∠DAC＝∠DBF,∠ADC＝∠BDF,随堂练习7.已知：如图，△ABC ≌△A′B′C′ ，AD，A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD＝ A′D′ ，并用一句话说出你的发现.随堂练习解：因为△ABC ≌△A′B′C′ ，所以AB=A'B'（全等三角形对应边相等），∠ABD=∠A'B'D'（全等三角形对应角相等）.因为AD⊥BC，A'D'⊥B'C'，所以∠ADB=∠A'D'B'.在△ABD和△A'B'D'中，∠ADB=∠A'D'B'（已证），∠ABD=∠A'B'D'（已证），AB=AB（已证），所以△ABD≌△A'B'D'（AAS）.所以AD=A'D'.随堂练习角边角和角角边内容有两角及夹边对应相等的两个三角形全等（简写成 “ASA”)应用为证明线段和角相等提供了新的证法注意注意“角角边”、“角边角”中两角与边的区别两角分别相等且其中一组等角的对边相等的两个三角形全等，（简写成 “AAS ” ）内容课堂小结课程结束