初中数学3 探索三角形全等的条件习题ppt课件

这是一份初中数学3 探索三角形全等的条件习题ppt课件，共24页。PPT课件主要包含了答案B，答案82°等内容，欢迎下载使用。

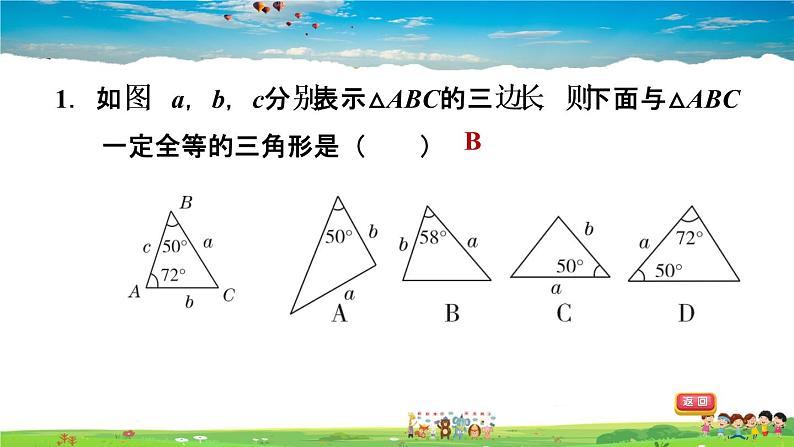
1．如图，a，b，c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（　　）
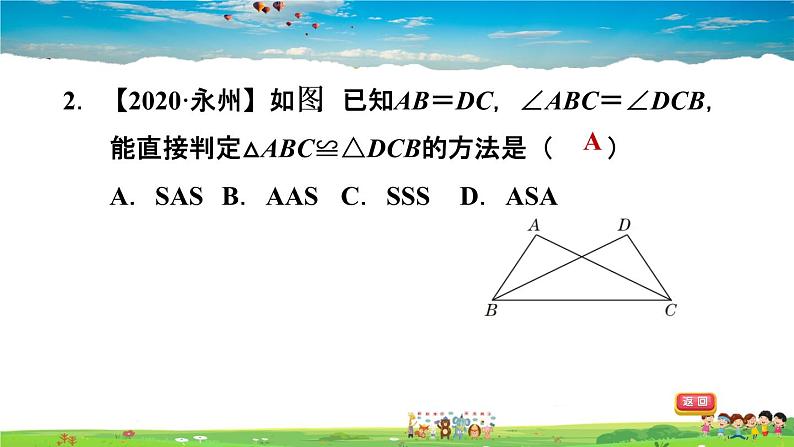
2．【2020·永州】如图，已知AB＝DC，∠ABC＝∠DCB，能直接判定△ABC≌△DCB的方法是（　　）A．SAS B．AAS C．SSS D．ASA
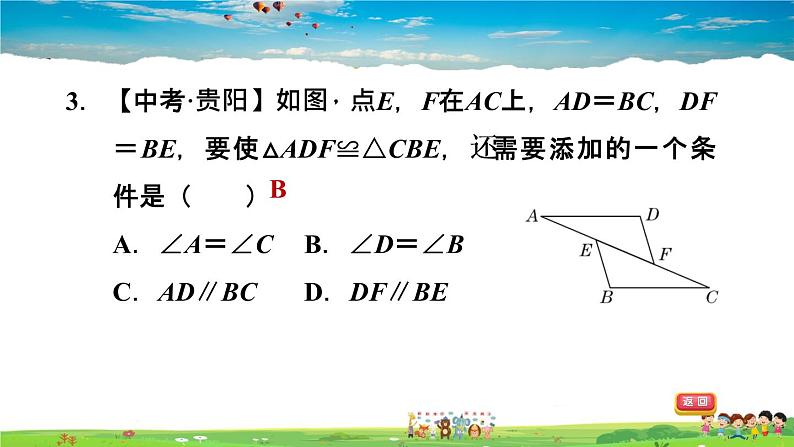
3．【中考·贵阳】如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（　　）A．∠A＝∠C B．∠D＝∠BC．AD∥BC D．DF∥BE
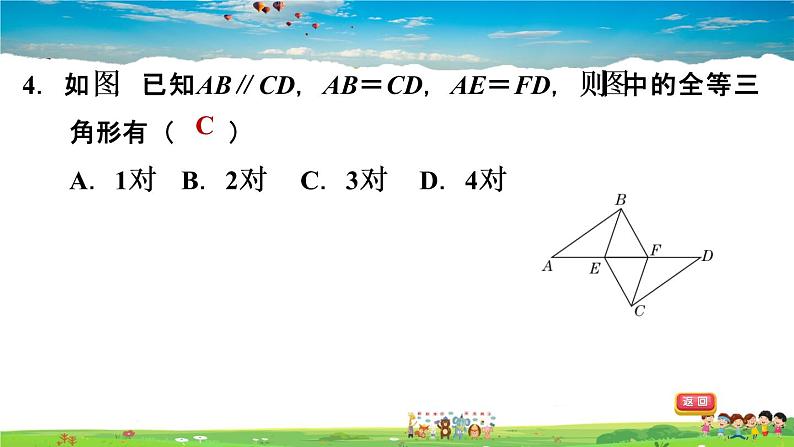
4．如图，已知AB∥CD，AB＝CD，AE＝FD，则图中的全等三角形有（　　）A．1对 B．2对 C．3对 D．4对
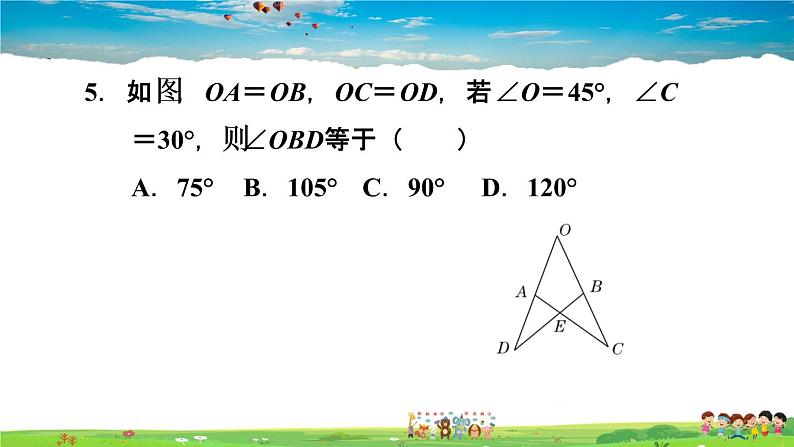
5．如图，OA＝OB，OC＝OD，若∠O＝45°，∠C＝30°，则∠OBD等于（　　）A．75° B．105° C．90° D．120°
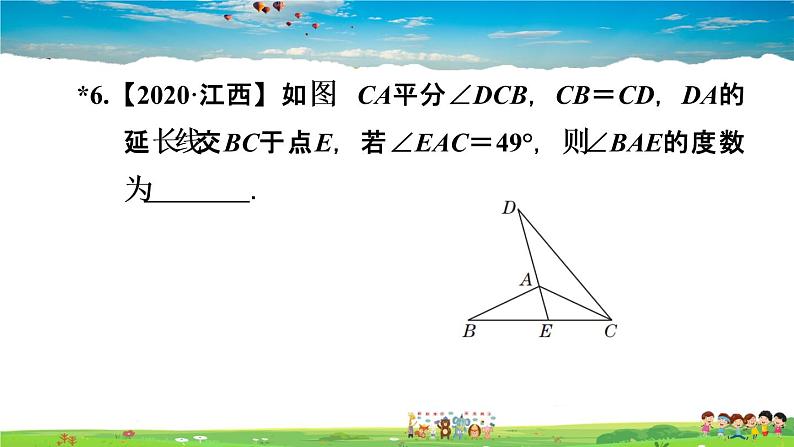
*6.【2020·江西】如图，CA平分∠DCB，CB＝CD，DA的延长线交BC于点E，若∠EAC＝49°，则∠BAE的度数为　　　　．
易说明△ABC≌△ADC，从而可得∠B＋∠ACB＝∠D＋∠ACD＝49°，进而根据三角形内角和定理求出∠BAC的度数，即可求出∠BAE的度数．
7．【2020·镇江】如图，AC是四边形ABCD的对角线，∠1＝∠B，点E，F分别在AB，BC上，BE＝CD，BF＝CA，连接EF. （1）试说明：∠D＝∠2；
解： 因为BE＝CD，∠1＝∠B，BF＝CA，所以△BEF≌△CDA(SAS)．所以∠D＝∠2.
（2）若EF∥AC，∠D＝78°，求∠BAC的度数．
解：因为∠D＝∠2，∠D＝78°，所以∠2＝78°.因为EF∥AC，所以∠BAC＝∠2＝78°.
8．如图，在△ABC中，AB＝AC，D，E分别是AB，AC的中点，且CD＝BE，△ADC与△AEB全等吗？请说明理由．
在说明两个三角形全等时，经常会出现用“SSA”判定两个三角形全等的情况．实际上，“SSA”不能判定两个三角形全等．因为两边及一边的对角分别相等的两个三角形不一定全等．如本题中易出现根据条件BE＝CD，AB＝AC，∠A＝∠A，利用“SSA”说明两个三角形全等的错误．
9．【2020·无锡】如图，已知AB∥CD，AB＝CD，BE＝CF.（1）试说明：△ABF≌△DCE；
解：因为AB∥CD，所以∠B＝∠C.因为BE＝CF，所以BE－EF＝CF－EF，即BF＝CE.又因为AB＝CD，所以△ABF≌△DCE(SAS)．
（2）试说明：AF∥DE.
解：因为△ABF≌△DCE，所以∠AFB＝∠DEC.所以∠AFE＝∠DEF.所以AF∥DE.
10．【2019·乐山】如图，线段AC，BD相交于点E，AE＝DE，BE＝CE.试说明：∠B＝∠C.
11．【2020·宜宾】如图，在△ABC中，点D是边BC的中点，连接AD并延长到点E，使DE＝AD，连接CE.（1）试说明：△ABD≌△ECD；
解：因为点D是边BC的中点，所以BD＝CD.又因为∠ADB＝∠EDC，AD＝ED，所以△ABD≌△ECD(SAS)．
（2）若△ABD的面积为5，求△ACE的面积．
解：在△ABC中，点D是边BC的中点，所以S△ABD＝S△ACD.因为△ABD≌△ECD，所以S△ABD＝S△ECD.因为S△ABD＝5，所以S△ACE＝S△ACD＋S△ECD＝5＋5＝10.
12．【2020·徐州】如图，AC⊥BC，DC⊥EC，AC＝BC，DC＝EC，AE与BD交于点F.（1）试说明：AE＝BD；
解：因为AC⊥BC，DC⊥EC，所以∠ACB＝∠DCE＝90°.所以∠ACE＝∠BCD.又因为AC＝BC，DC＝EC.所以△ACE≌△BCD(SAS)．所以AE＝BD.