
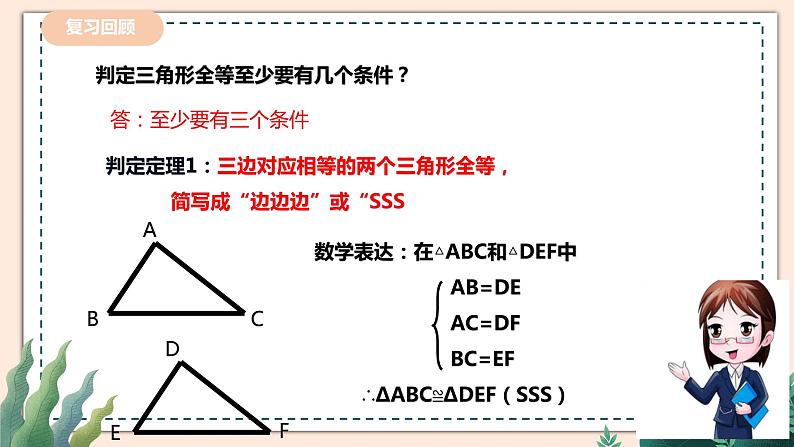





- 4.2 《图形的全等》 课件+教案 课件 16 次下载
- 4.3.1《探索三角形全等的条件》 课件+教案 课件 15 次下载
- 4.3.3《探索三角形全等的条件》 课件+教案 课件 18 次下载
- 4.4 《用尺规作三角形》 课件+教案 课件 15 次下载
- 4.5 《利用三角形全等测距离》 课件+教案 课件 14 次下载
初中数学北师大版七年级下册3 探索三角形全等的条件完整版课件ppt
展开北师版数学七年级下4.3.2探索三角形全等的条件教案
课题 | 4.3.2探索三角形全等的条件 | 单元 | 4 | 学科 | 数学 | 年级 | 七 |
学习 目标 | 1.探索并掌握两个三角形全等的条件:“ASA”,“AAS”. 2.并能应用它们判别两个三角形是否全等。 | ||||||
重点 | 掌握三角形全等的条件“ASA”“AAS”,并能应用它们来判定两个三角形是否全等 | ||||||
难点 | 用三角形“角边角”“角角边”的条件进行有条理的思考和简单的推理。 | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
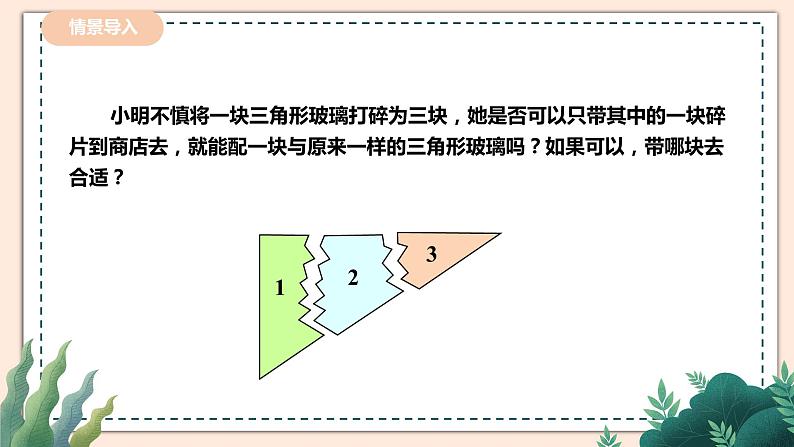
导入新课 | 如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与 原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗? |
思考 自议
| 通过创设问题情景,激发了学生探究新知的热情。 |
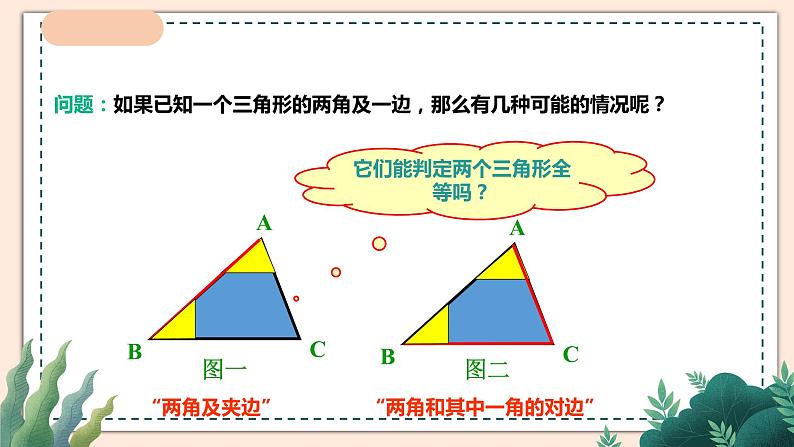
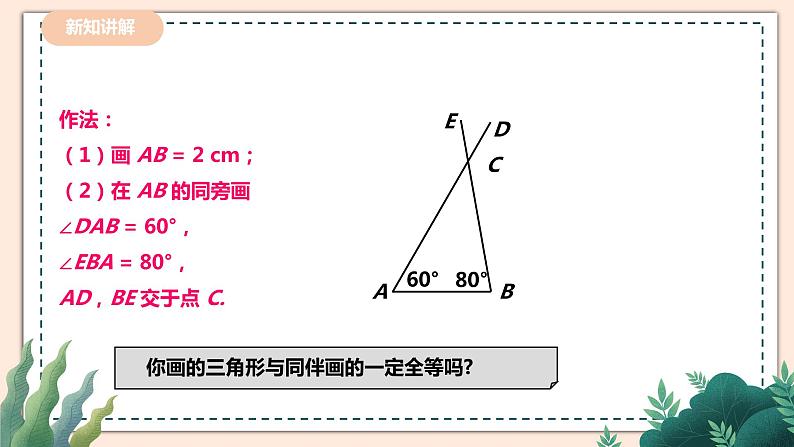
讲授新课 | 【做一做】 如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗? 【做一做】 测量、画三角形。同学们交流一下画这个三角形的步骤. 方法1:先画出BC=2 cm,然后画∠B=80°,最后画∠C=60°.
方法2:先画出∠B=80°,然后画BC=2 cm,最后画∠C=60°. 同学把画出的三角形剪下来,与同小组比较,看是否重合. 画出的三角形都全等. 改变角度和边长,你能得到同样的结论吗? 【总结归纳】 两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”. 几何语言: 在△ABC和△DEF中, ∠A=∠D, AB=DE, ∠B=∠E , ∴△ABC≌△DEF(ASA). 议一议 如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢? 你能将它转化为“做一做”中的条件吗? 【做一做】 如果“两角及一边”条件中的边是其中一角的对边,比如三角形的两个内角分别是60°和80°,其中60°角所对的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗? 【总结归纳】 两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS”. 几何语言: 在△ABC和△DEF中, ∠A=∠D, ∠B=∠E , AB=DE ∴△ABC≌△DEF(ASA). 例、如图所示,AB 与 CD 相交于点 O,O 是 AB 的中点,∠A = ∠B,△AOC 与△BOD 全等吗?为什么? 【总结提升】 在说明两个三角形全等所需要的角相等时,目前通常采用的方法有: (1)公共角、对顶角分别相等; (2)等角加(减)等角,其和(差)相等,即等式的性质; (3)同角或等角的余(补)角相等;(4)角平分线得到相等角; (5)平行线的同位角、内错角相等;(6)直角都相等; (7)全等三角形对应角相等;(8)第三角代换,即等量代换等. 解决导入问题: 小明不慎将一块三角形玻璃打碎为三块,她是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃吗?如果可以,带哪块去合适? |
改变角度和边长,所画的三角形仍然全等。
学生在教师的引导下总结归纳。
根据教师提供的条件画一画,然后和同桌比较所画的三角形是否全等。
学生在教师的引导下总结归纳。
学生根据所系知识做例题。巩固所学知识。
学生解决问题
| 通过实践操作,使学生对三角形全等条件有了一个更清楚的理解,让学生懂得数学就来自于我们的生活,体会到数学与我们生活的联系.让学生逐步深入,符合学生的认知规律,培养学生的创新精神,增强学生的合作意识.
通过老师引导、学生在活动中归纳总结。培养学生的语言表达能力。
通过实践操作,使学生对三角形全等条件有了一个更清楚的理解,让学生懂得数学就来自于我们的生活,体会到数学与我们生活的联系.
通过老师引导、学生在活动中归纳总结。培养学生的语言表达能力。
安排具有一定挑战性的分析、表达题,引导学生熟练掌握角形全等的“ 角边角”条件。逐步培养学生推理意识和能力
再次巩固新知
|
课堂练习 | 1.如图,已知:∠A=∠D,要使△ABC≌△DCB,只需增加一个条件是( ) A.AC=DB B.BC=CB C.∠ABC=∠DCB D.AB=DC 2. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°,且AC=A′C′,那么这两个三角形( ) A.一定不全等 B.一定全等 C.不一定全等 D.以上都不对 3. 如图,已知∠A =∠D,AB = CD,可得△ABO≌_______,理由是______. 4、如图,已知AB=DE, ∠A =∠D, ,∠B=∠E,则 △ABC ≌△DEF的理由是: 。 5.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
|
学生自主完成习题,老师订正 |
让学生巩固已学知识,加深对知识的理解与运用 |
课堂小结 | 1.知识回顾. 2.谈谈这节课你有哪些收获? | 教师与学生一起进行交流,共同回顾本节知识 | 让学生与同伴交流获得结果,帮助他分析,找出问题原因,及时查漏补缺. |
板书 | 两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”. 两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”. |
|
|
初中数学3 探索三角形全等的条件图片ppt课件: 这是一份初中数学3 探索三角形全等的条件图片ppt课件,共25页。PPT课件主要包含了角角边,ASA,公共边,∠2∠1,AAS等内容,欢迎下载使用。
北师大版七年级下册3 探索三角形全等的条件教课ppt课件: 这是一份北师大版七年级下册3 探索三角形全等的条件教课ppt课件,文件包含432探索三角形全等的条件pptx、43探索三角形全等的条件第2课时利用“角边角”“角角边”判定三角形全等doc等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学北师大版七年级下册3 探索三角形全等的条件获奖课件ppt: 这是一份初中数学北师大版七年级下册3 探索三角形全等的条件获奖课件ppt,文件包含433探索三角形全等的条件pptx、北师版数学七年级下433探索三角形全等的条件教案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。













