初中数学人教版八年级上册13.1.1 轴对称教学课件ppt

这是一份初中数学人教版八年级上册13.1.1 轴对称教学课件ppt，共19页。PPT课件主要包含了专题讲解，P-30，拓展提升，∵CDAE等内容，欢迎下载使用。

轴对称复习 (第2课时)
专题一 轴对称及轴对称图形
专题二 线段垂直平分线的性质和判定
专题三 等腰三角形的性质和判定
专题四 将军饮马和造桥选址问题
例1 下列“禁止行人通行、注意危险、禁止非机动车通行、限速60 km/h”四个交通标志图中，为轴对称图形的是（　　）
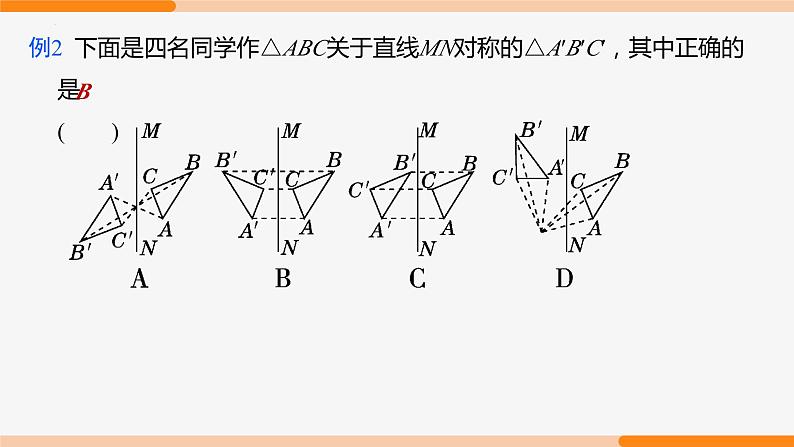
例2 下面是四名同学作△ABC关于直线MN对称的△A′B′C′，其中正确的是 (　　)
例3.已知点M(2a－b，5＋a)，N(2b－1，－a＋b)．(1)若点M，N关于x轴对称，试求a，b的值；(2)若点M，N关于y轴对称，试求(b＋2a)99的值．
例1 在△ABC中，AD是高，在线段DC上取一点E，使BD=DE，已知AB+BD=DC.求证：点E在线段AC的垂直平分线上．
证明：∵ AD是高，∴AD⊥BC.又∵BD=DE，∴AD所在的直线是线段BE的垂直平分线，∴AB=AE，∴AB+BD=AE+DE.又∵AB+BD=DC，
∴DC=AE+DE，∴DE+EC=AE+DE,∴EC=AE，∴点E在线段AC的垂直平分线上．
例2.如图，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
证明：如图，连接AF.∵AB=AC，∠BAC=120°，∴∠B=∠C=30°.∵AC的垂直平分线是EF，∴CF=AF，∴∠FAC=∠C=30°，
∴∠BAF=∠BAC-∠FAC=120°-30°=90°.在Rt△ABF中，∠B=30°，∴BF=2AF，∴BF=2CF．
例1 等腰三角形的一个内角是另一个内角的2倍，求该等腰三角形的顶角的度数.
解：设该等腰三角形中，小角的度数为x,则大角的度数为2x.
当x为底角时， x +x+ 2x=180°， 解得 x=45°，则2x=90°.
当x为顶角时， x +2x+ 2x=180°， 解得x =36°.
故该等腰三角形顶角的度数为90°或36°.
证明：过点E作EG∥AC交BC于点G，如图，则∠1＝∠F，∠2＝∠3.∵ AB＝AC，∴ ∠B＝∠3(等边对等角)．∴ ∠B＝∠2.∴ BE＝EG(等角对等边)．又∵BE＝CF，∴ EG＝CF.
例2.如图，在△ABC中，AB＝AC，EF交AB于点E，交AC的延长线于点F，交BC于点D，且BE＝CF. 求证：DE＝DF.
在△EDG和△FDC中， ∠1＝∠F，∠4＝∠5，EG＝ FC，∴ △EDG≌△FDC(AAS)．∴ DE＝DF.
例3 如图，∠AOP＝∠BOP＝15°，PC∥OA交OB于C，PD⊥OA于D，若PC＝3，求PD的长.
解 如图，过点P作PE⊥OB于E.∵ PC∥OA，∴∠PCE＝∠AOB＝∠BOP＋∠AOP＝30°.又∵ PC＝3，∴ PE＝1.5.∵ ∠AOP＝∠BOP，PD⊥OA，∴ PD＝PE＝1.5.
例1 按要求完成作图：(1)作△ABC关于y轴对称的△A1B1C1；(2)在x轴上找出点P，使PA+PC最小，并直接写出P点的坐标：
例2 如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是（　　）A．10 B．15C．20 D．30
1.将如图的七巧板的其中几块，拼成一个多边形，为轴对称图形的是( )
2.在平面直角坐标系中，若点P(a－3，1)与点Q(2，b＋1)关于x轴对称，则a＋b的值是(　　)A．1 B．2C．3 D．4
4.如图，已知在△ABC中，AB＝AC，∠C＝30°，AB⊥AD，则下列关系式正确的为(　　) A．BD＝CD B．BD＝2CD C．BD＝3CD D．BD＝4CD
3.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC = .
5.如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC、∠BCD的平分线，则图中的等腰三角形有(　　)A．5个 B．4个 C．3个 D．2个
6.一个三角形的一个外角为130°，且它恰好等于一个不相邻的内角的2倍，则这个三角形是（ ）A．钝角三角形 　 B．直角三角形 　C．等腰三角形 　 D．等边三角形
7 如图，在△ABC中，AB=AC,BD⊥AC于D.求证： ∠BAC=2∠DBC.
证明：作∠BAC的平分线AE,交BC于点E,如图所示，则
∵ AB=AC, ∴ AE⊥BC.
∴ ∠2+ ∠ACB=90 °.
∵ BD⊥AC, ∴ ∠DBC+ ∠ACB=90 °.
∴ ∠2= ∠DBC.
∴ ∠BAC= 2∠DBC.
7.如图,在△ABC中,AD是角平分线,AC=AB+BD.求证：∠B=2∠C.
证明：在AC上截取AE=AB，连接DE.
∵AD是角平分线，∴∠EAD=∠BAD.
又∵AD=AD，∴△EAD≌△BAD，∴DE=DB，∠AED=∠B.
∵AC=AB+BD=AE+DE=AE+EC，∴CE=ED.
∴∠AED=∠C+∠CDE=2∠C，即∠B=2∠C.
想一想：还有别的证明方法吗？
提示：延长AB至F，使BF=BD，连接DF.
8.如图，已知△ABC是等边三角形，D，E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q.求证：BP=2PQ.
∴△ADC≌△BEA.
证明：∵△ABC为等边三角形，
∴ AC=BC=AB ，∠C=∠BAC=60°.