人教版八年级上册13.1.1 轴对称精品教案设计

第十三章 《轴对称》复习教学设计

一；教学目标

1.知识的整理和归纳。

2. 掌握线段的垂直平分线、角的平分线的性质及应用，理解等腰三角形，等边三角形的性质并能够简单应用，能利用轴对称的性质解决问题。

3.体会轴对称的“桥梁”作用，感悟转化思想。

二．教学重点

1.知识的整理和归纳。

2. 理解等腰三角形，等边三角形的性质并能够简单应用，利用轴对称的性质解决问题。

三．教学难点

利用轴对称的性质解决问题。

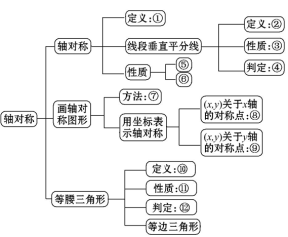
1.本章知识结构图

   2.有关概念复习

（1）轴对称；（2）轴对称图形；

①．如果____ ____沿一条直线折叠,直线两旁的部分能够_________,这个图形就叫做轴对称图形.这条直线就是它的_______.这时我们也说这个图形关于这条直线（成轴）对称。

②．把_____  __沿着某一条直线折叠,如果它能够与__  ___图形__ __,那么就说这两个图形关于这条直线（成轴）对称.这条直线叫做_ ____，折叠后重合的点是对应点,叫做__ ____.

③用表格的方式对比两种图形的区别和联系.

设计意图：通过复习回顾，学生回忆思考，提高他们的观察，分析，归纳，概括，对比的能力。

练习1.下列四个艺术字中，不是轴对称的是(　　)

设计意图：轴对称图形的判断，使学生加深对定义的理解。

（3）轴对称的性质

①．如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的              。

②．对称轴两侧的图形关系为             

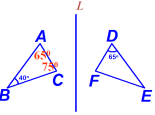
练习2. △ABC与△DEF关于直线L成轴对称，

则∠C是多少度？

设计意图：轴对称的性质应用，通过图形的不变性，掌握解决基本几何图形问题的方法。

（4）线段的垂直平分线

①．形 ：点P在线段AB的垂直平分线MN上   ＝＞ PA=PB  （性质）

数： PA=PB ＝＞  点P在线段AB的垂直平分线MN上   （判断）

②．直线MN可以看成与线段AB两端点

A、B的距离相等的所有点的______.

练习3.下列说法错误的是（    ）

A.过“到线段两端点距离相等的点”的直线是线段的垂直平分线

B.线段垂直平分线的点到线段两端点的距离相等

C.线段有且只有一条垂直平分线

D.线段的垂直平分线是一条直线

练习4.如图，已知在△ABC中，AB=AC=10，DE垂直平分AB，

垂足为E，DE交AC于D，若△BDC的周长为16，则BC=　____．

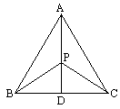
练习5.如图：△ABC中,AB=AC,PB=PC．

求证：AD⊥BC

设计意图：考察垂直平分线的性质，提升学生灵活运用的能力。通过几何证明的方式，培养学生逻辑思维能力。

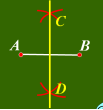3.线段的垂直平分线作法

①确定线段的中点作法                  

②作两点的对称轴作法

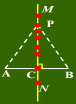
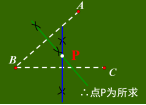
应用：如图点A、B、C表示三个小区，现要修建一个购物中心，

使它到三个小区的距离相等，求购物中心的位置P.

三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等。

设计意图：全面考察学生对垂直平分线的做法及运用，并解决相关的实际问题。

4.画轴对称图形的方法

对于某些图形，只要_____图形中的一些特殊点（如线段端点）

的对称点，_____这些对称点，就得到原图形的轴对称图形．

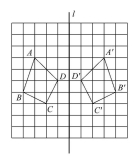练习6.如图，在边长为1的小正方形组成的10×10网格

中四边形ABCD在直线l的左侧，其四个顶点A，B，C，D

分别在网格的格点上.

（1）画图形关于x轴或y轴对称图形的方法

①.运用轴对称图形的性质作图      ②.运用坐标变化的规律作图

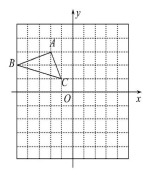点(x, y)关于x轴对称的点的坐标为(x,－y)

点(x, y)关于y轴对称的点的坐标为(－x,y)

练习7.如图，△ABC在平面直角坐标系中第二象限内，

顶点A的坐标是(-2，3)，求作△ABC关于x轴对称的图形△A1B1C1.

练习8.点A(-3，0)关于y轴的对称点的坐标是　　　　.

练习9.已知两点的坐标分别是      （﹣2，3）和（2，3），则下列情况：其中正确的有（　　）

①点关于x轴对称  ②两点关于y轴对称  ③两点之间距离为4．

A.3个      B.2个       C.1个      D.0个

设计意图：应用关于x轴、y轴对称的点的坐标的规律，解决简单的问题，从中体会利用点的坐标解决轴对称问题的思想方法。

5.等腰三角形（1）等腰三角形的定义：                    

有两边相等的三角形叫___________   

性质：等腰三角形的顶角平分线、 底边上的中线、底边上的高互相重合.（三线合一）

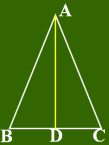1、如图，在△ABC中，AB=AC时，    

(1)∵AD⊥BC∴∠ ____= ∠_____;____=____

(2) ∵AD是中线∴____⊥____; ∠_____= ∠_____

(3) ∵ AD是角平分线∵____ ⊥____;_____=____

练习10.若等腰三角形的两边长为 2 cm和7 cm，则等腰三角形的周长为　 cm.

练习11.等腰三角形一腰上的高与另一腰的夹角为40°，则其顶角为             

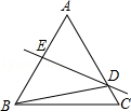
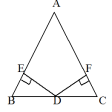
练习12.已知：如图，在△ABC中，AB＝AC，D是BC的中点，

DE⊥AB，DF⊥AC，E、F分别是垂足。求证：AE＝AF。                 

设计意图：等腰三角形的应用，在练习中让学生掌握好分类讨论的思想。

（2）等腰三角形的判定:

①.________的三角形是等边三角形.

②.如果一个三角形有_________，  那么两个角所对的边也相等，则这个三角形是等边三角形.（等角对等边）

（3）等边三角形的判定:

①. _________的三角形是等边三角形.

②.__________的三角形是等边三角形.

③. 有__________的__________是等边三角形.

练习13.下列四个说法中，正确的有（    ）

①三个角都相等的三角形是等边三角形；②有两个角等于60°的三角形是等边三角形；                                                           ③有一个是60°的等腰三角形是等边三角形；                                                           ④有两个角相等的等腰三角形是等边三角形。A.0个B.1个C.2个D.3个

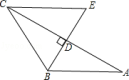练习14.已知：如图，在△ABC中，AB=BC，∠ABC=120°，

BE⊥AC于点D，且DE=DB，试判断△CEB的形状，并说明理由

设计意图：综合运用等腰三角形的判定方法，并在解答题中让学生完整的叙述和证明。

（4）特殊三角形性质的判定:

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.

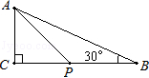练习15.如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（　　）

A  3.5     B  4.2     C  5.8     D   7　

设计意图：灵活运用特殊三角形的性质判定，并求出三角形的基本元素

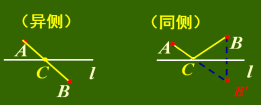5.最短路径问题的基本模型：

①.点到点：两点之间，线段最短

②.点到线：垂线段最短 ③.两点一线

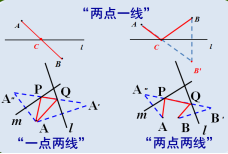
变式1：利用轴对称变换，

把“折”路径摆成“直”路径.

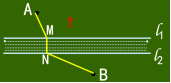变式2：造桥选址问题

如图,A和B两地在一条河的两岸,现要在河

上造一座桥MN,桥应造在何处才能使从A

到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)

设计意图：通过不同的类型，考察学生是否能够识别并解决这类实际问题。

四；课堂小结

1．同学们通过这节课的复习，你能否迅速的说出本章你所掌握的知识点？

2.你能否归纳本章的题型，且对本章的作图题归纳出简单的步骤？

设计意图：通过讨论、交流，加深对所学知识的认识，锻炼学生自主归纳小结的能力。

五.作业布置：

课本第91-93页，第8，9，10题