苏科版八年级上册第一章 全等三角形1.2 全等三角形精品导学案
展开1.2全等三角形
【学习目标】
基本目标:1.知道全等形的概念,并会用符号表示两个三角形全等
2.知道全等三角形的有关概念,会在两个全等三角形中正确找出对应顶点、对应边、对应角
提升目标:理解全等三角形的对应边、对应角相等的性质,能进行简单推理。
【重点难点】
重点:全等三角形的性质及其应用.
难点:确认全等三角形的对应元素,理解平移、翻折、旋转等全等变换的过程.
【课堂导学】
一、情境引入
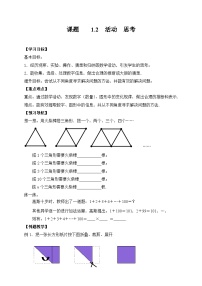
想一想:观察下列图形:
(图1) (图2) (图3)
图1是△ABC经过 得到△DEF;
图2是△ABC绕着 后得到△ADE;
图3是△ABD沿边 后得到△ADC;
1.上图中的三组三角形有什么特征?
2.在△ABC通过变化与另一个三角形重合时,你能分别说出与点A、B、C重合的点吗?
3.你能写到每组图形中有哪些相等的数量关系吗?
知识点归纳:
1、全等三角形的表示方法(如右图): 。
2、全等三角形的性质: 。
数学符号语言(如右图):
∵ ≌
∴AB= , AC= , BC = .
∠ = , = , = .
3、注意点:表示两个三角形全等时,通常把对应顶点的字母写在 .
二、例题讲解
例1、若下列图形中的两个三角形为全等三角形,请用符号表示出图中的全等三角形,并写出对应边和对应角。
(1) (2) (3)
例2、如图△ABC ≌ △DCB
(1)写出∠ACB的对应角和BC的对应边。
(2)若∠A=100°, ∠DBC=20°,求∠ABC 和∠DOC的度数 .
例3、已知:如图△ABC≌△ADE,试判断图中∠1与∠2的关系,说明理由.
【课堂检测】
- 如图1,将△ABC绕顶点A旋转一定角度得到△ADE,那么△ABC ≌ ________,AB=_________, AC=_________,CB=_________,∠B=________,∠BAC=_______,
∠BAD=________.
2. 如图2,△ABC ≌△ADC,若∠BAC=°,∠B=°,则∠DAC= °,
∠ACD= °,∠D= °
图1 图2 图3
3. 如图3,△ABE≌△DBC,AB=3cm,DE=2cm,求BC的长.
【课后巩固】
一、夯实基础
1. 已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
(1) (2)
2. 如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2 B.AC=CA C.AC=BC D.∠D=∠B
3. 如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.
(1)BD是∠ABE的平分线吗?为什么?
(2)DE⊥BC吗?为什么?
(3)点E平分线段BC吗?为什么?
二、加强理解
4. 如图所示,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
5.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°, ∠EAB=120°,求∠DFB和
∠DGB的度数.
三、拓展思维
6.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠1:∠2:∠3=28:5:3,求∠EFC的度数.
初中数学苏科版八年级上册4.4 近似数优质导学案: 这是一份初中数学苏科版八年级上册4.4 近似数优质导学案,共5页。学案主要包含了学习目标,教学重难点,预习导航,课堂导学,课堂检测,课后巩固等内容,欢迎下载使用。
初中苏科版4.2 立方根精品学案设计: 这是一份初中苏科版4.2 立方根精品学案设计,共3页。学案主要包含了复习回顾,合作探究,当堂反馈,课堂小结,课后作业等内容,欢迎下载使用。
苏科版八年级上册3.1 勾股定理精品导学案: 这是一份苏科版八年级上册3.1 勾股定理精品导学案,共4页。学案主要包含了学习目标,学习重点,学习难点,学习过程,【拓展延伸】等内容,欢迎下载使用。