


2023八年级数学下册第1章直角三角形角平分线的判定同步练习新版湘教版
展开1.4.2角平分线的判定同步练习
一、选择题(本大题共8小题)
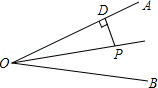
1. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B. 5 C. 4 D. 3
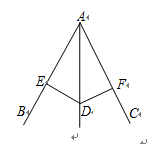
2.如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,下列结论中不正确的是( )
A.DE=DF B.AE=AF
C.△ADE≌△ADF D.AD=DE+DF
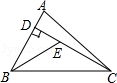
3. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B. 7 C. 5 D. 4
4. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A.![]() B. 2 C. 3 D.
B. 2 C. 3 D. ![]() +2
+2

5. 已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB边的距离为( )
A.18 B.16 C.14 D. 12
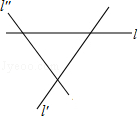
6. 如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B. 二处 C. 三处 D. 四处
7. 在△ABC中,∠B=∠ACB,CD是∠ACB的角平分线,已知∠ADC=105°,则∠A的度数为( )
A.40° B.36° C.70° D.60°
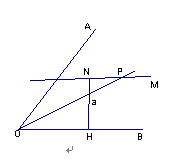
8. 如图, ∠AOB和一条定长线段A,在∠AOB内找一点P,使P 到OA、OB的距离都等于A,做法如下:(1)作OB的垂线NH,使NH=A,H为垂足.(2)过N作NM∥OB.(3)作∠AOB的平分线OP,与NM交于P.(4)点P即为所求.其中(3)的依据是( )
A.平行线之间的距离处处相等
B.到角的两边距离相等的点在角的平分线上
C.角的平分线上的点到角的两边的距离相等
D.到线段的两个端点距离相等的点在线段垂直平分线上
二、填空题(本大题共6小题)
9. 已知△ABC中,∠A=80°,∠B和∠C的角平分线交于O点,则∠BOC= 。
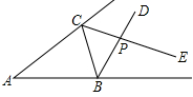
10. 如图,△ABC的∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,若点P到AC的距离为4,则点P到AB的距离为 .
11. 如图,△ABC中,∠C=90°,∠A=36°,DE⊥AB于D,且EC=ED,
∠EBC= °

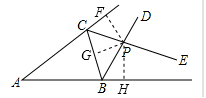
12. 如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是 。

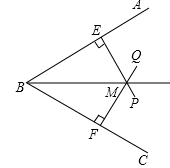
13. 如图,点M在∠ABC内,ME⊥AB于E点,MF⊥BC于F点,且ME=MF,∠ABC=70°,则∠BME= °.
三、计算题(本大题共4小题)
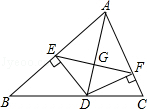
14. 如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.
15. 如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.

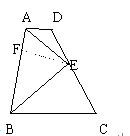
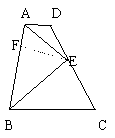
16. 如图,已知AD∥BC, ∠DAB和∠ABC的平分线交于E, 过E的直线交AD于D, 交BC于C, 求证: DE=EC.
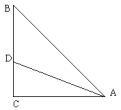
17. 如图16所示,已知AD为等腰三角形ABC的底角的平分线,∠C=90°,求证:AB=AC+CD.
参考答案:
一、选择题(本大题共8小题)
1. A
分析:过点p作PE⊥OB于点E。根据角平分线上的点到角的两边的距离相等可解答得到。
解:解:过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PD=6,
∴PE=6,
即点P到OB的距离是6.
故选:A.
2.D
分析:题目的已知条件比较充分,满足了角平分线的性质要求的条件,可直接应用性质得到结论,与各选项进行比对,得出答案.
解:∵P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,
∴PE=PF,又有AD=AD
∴△APE≌△APF(HL)
∴AE=AF故选D.
3. C
分析:角平分线的性质.
解:作![]() 于F,
于F,![]() 平分
平分![]()
![]()
![]() 故选C.
故选C.
4. C
分析:运用在直角三角形中,30°角所对的直角边是斜边的一半来求解。
解: ∠B=30° BD=2DE=2 ∠CAD=30° CD=BD/2=1 BC=CD+BD=1+2=3.故选C
5. C
分析:做DE垂直于AB,求证ΔACD全等ΔAED(AAS),CD等于DE,用比例设X,求出CD,BD长,DE就是距离。
解:如图,过D作DE⊥AB于E,
∵AD平分∠BAC交BC于D,而∠C=90°,
∴CD=DE,
∵BC=64,且BD:CD=9:7,
∴CD=64×![]() =28,∴DE=28,
=28,∴DE=28,
则点D到AB边的距离为28.故选C.

6. D
分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
解:如图所示,加油站站的地址有四处.
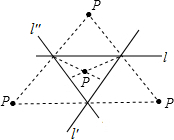
故选D.
7. 在△ABA
分析:可根据角平分线的性质及其三角形外角的性质列方程解答。
解:因为∠B=∠ACB,故可设∠B=∠ACB=x,则根据题意列方程得到:![]() x=105°, ∠B=∠ACB=70°, ∠A的度数40°,故选A。
x=105°, ∠B=∠ACB=70°, ∠A的度数40°,故选A。
8. B
分析:题目要求满足两个条件,其一是到角OA,OB的距离相等,作角平分线,根据到角的两边距离相等的点在角平分线上,可得答案.
解:根据角平分线的性质,(3)的依据是到角的两边的距离相等的点在角平分线上,
故选B.
二、填空题(本大题共6小题)
9. 分析:本题考查的是角平分线的性质,利用角平分线分角成一半和三角形内角和定理或连接AO并延长,利用三角形的外角性质
解:因为∠A=80°,∠B的平分线与∠C的平分线交点O,
则∠B+∠C=180°-80=100°,∠BOC=180°-(∠B+∠C)÷2=180°-50°=130°.
10. 分析:过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,然后根据角平分线上的点到角的两边的距离相等可得PF=PG=PH,从而得解
解:如图,过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,
∴PF=PG=4,PG=PH,
∴PF=PG=PH=4.故答案为:4.
11. 解:∵∠C=90°,∠A=36°,
∴∠ABC=54°,
又∵∠C=90°,DE⊥AB于D,且EC=ED,
∴BE平分∠ABC,
∴∠EBC=27°.
故答案为:27.
12. 分析:根据角平分线性质:角平分线上的点到角的两边距离相等即可得到结果
解:根据角平分线性质:角平分线上的点到角的两边距离相等即可得到结果,
![]() BD是∠ABC的内角平分线,DE⊥BC、DG⊥AB,
BD是∠ABC的内角平分线,DE⊥BC、DG⊥AB,![]()
![]() CD是∠ACB的外角平分线,DE⊥BC、DF⊥AC,
CD是∠ACB的外角平分线,DE⊥BC、DF⊥AC,![]()
![]()
13. 分析:根据到角的两边距离相等的点在角的平分线上判断出BM平分∠ABC,然后求出∠ABM,再根据直角三角形两锐角互余求解即可.
解:解:∵ME⊥AB,MF⊥BC,ME=MF,
∴BM平分∠ABC,
∴∠ABM= ![]() ∠ABC=
∠ABC= ![]() ×70°=35°,
×70°=35°,
∴∠BME=90°-∠ABM=90°-35°=55°.
故答案为:55°.
三、计算题(本大题共4小题)
14. 分析:![]()
证明:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD.
在△AED和△AFD中,
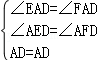 ,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF.
15. 证明:(1)如图,连接AP并延长,
∵PE⊥AB,PF⊥AC
∴∠AEP=∠AFP=90°
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
![]()
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.

16.证:在AB上截取AF=AD。∵AE是∠DAF的平分线(已知)
∴∠DAE=∠FAE(角平分线定义)
在△DAE和△FAE中, ∴△DAE≌△FAE(SAS)
∴△DAE≌△FAE(SAS)
∴DE=FE(全等三角形对应边相等)∴∠D=∠AFE(全等三角形对应角相等)
∵∠AFE+∠BFE=1800(邻补角定义)
又AD∥BC(已知)
∴∠D+∠C=1800(两直线平行,同旁内角互补)
∴∠BFE=∠C(等角的补角相等)
∵BE是∠ABC的平分线(已知)∴∠FBE=∠CBE(角平分线定义)
在△FBE和△CBE中 ∴△FBE≌△CBE(AAS)
∴△FBE≌△CBE(AAS)
∴FE=CE(全等三角形对应边相等) ∴DE=EC.
17. 证明:证一(截长法):如图1所示,过点D作BD⊥AB于E,
∵AD是∠BAC的平分线
 ∴∠CAD=∠EAD,又∠DEA=∠DCA且AD公共,∴△ADE≌△ACD(AAS),∴ AE=AC,CD=DE
∴∠CAD=∠EAD,又∠DEA=∠DCA且AD公共,∴△ADE≌△ACD(AAS),∴ AE=AC,CD=DE
在△DEB中,∵∠B=45°,∠DEB=90°,
∴△EBD是等腰直角三角形.∴DE=EB,∴CD=EB.
∴AC+CD=AE+EB,即AC+CD=AB.
证法二(补短法):
如图2所示,在AC的延长线上截取CM=CD,连结DM.
在△MCD中,∠MCD=90°,CD=CM
∴△MCD是等腰直角三角形.∴∠M=45°
又∵在等腰直角三角形中,∠B=45°
∴∠M=∠B=45° 又∵AD平分∠CAD
∴在△MAD与△BAD中
∴△MAD≌△BAD(AAS)∴MA=AB,即AC+CD=AB.









