
数学八年级下册2.5.2矩形的判定优秀教案
展开2.5.2 矩形的判定
![]()
【知识与技能】
1.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力.
2.通过矩形判定的教学渗透矛盾可以互相转化的唯物辩证法思想.
【过程与方法】
经历矩形的判定的探究过程,并能有效的解决问题,培养学生的逻辑思维能力和演绎能力.
【情感态度】
通过矩形判定的推导证明,培养学生热爱数学和生活中的图形,锻炼克服困难的意志,建立自信心.
【教学重点】
矩形判定方法的探究与运用
【教学难点】
矩形的性质与判定的综合运用
![]()
一、创设情境,导入新课
李芳同学用“边——直角、边——直角、边——直角边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
【教学说明】情境引入激发学生的兴趣,通过让学生画图,激起疑惑.教师讲课前,先让学生完成预习.
二、思考探究,获取新知
问题 矩形的判定
思考 教材第61页上“动脑筋”
【教学说明】让学生验证三个角是直角的四边形是矩形,从而得到矩形的第二种判定方法.
思考 教材第61页下“动脑筋”
【教学说明】使学生经历画图验证、说理的过程,让学生明白对角线相等的平行四边形也是矩形,从而得到理解的第三种判定方法.
例:教材第62页“例2”
【教学说明】运用所学的矩形的性质与判定解决问题,既起到巩固新知识的作用,又教会了学生把题中的条件能灵活的转化,体验转化的思想.
三、运用新知,深化理解
1.已知四边形ABCD的对角线AC、BD相交于点O,那么下列条件中,不能判定四边形ABCD为矩形的是( )
A.∠BAD=∠ABC=∠BCD=∠ADC
B.OA=OB=OC=OD
C.AB=CD,AD=BC,AC=BD
D.∠BAD=∠BCD,∠ABC+∠BCD=180°,∠AOB=∠BOC
2.M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,当AB、BC满足条件 时,四边形PEMF为矩形.
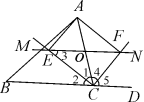
3.如图所示,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO.
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
【教学说明】让学生独立完成,便于教师了解学生的掌握情况,及时辅导有困难的学生,出错较多的地方要作必要的强调补充,好的解题方法应大力表扬.在完成上述题目后,让学生完成练习册中本课时的对应训练部分.
答案:1.D 2.BC=2AB
3.(1)证明:∵CE平分∠ACB,
∴∠1=∠2,∵EF∥BC,∴∠2=∠3,
∴∠1=∠3,∴EO=OC,
同理OF=OC,∴EO=FO.
(2)解:当O运动到AC中点时,四边形AECF为矩形,
证明:∵AO=CO,又∵EO=FO,
∴四边形AECF为平行四边形,
又∵EC、FC平分∠ACB、∠ACD,
∠1+∠2+∠4+∠5=180°,
∴∠1+∠4=90°,
∴□AECF是矩形.
四、师生互动,课堂小结
到目前为止,你已经学习了矩形的哪几种判定方法?还有什么心得体会?与大家共同分享.
【教学说明】让学生学会归纳总结,整理形成知识体系,培养学生良好的学习习惯.同学之间相互交流,共同提高.
![]()
1.布置作业:习题2.5中的第3、4题.
2.完成练习册中本课时练习的作业部分.
![]()
就学生的掌握情况来看,对于运用矩形的判定方法进行有关的证明和计算,比较容易一些,而对于矩形的性质与判定的综合应用还比较欠缺.在今后的教学中要通过实例让学生不断加以强化,促进全面提高.
初中数学2.5.2矩形的判定教案设计: 这是一份初中数学<a href="/sx/tb_c95354_t8/?tag_id=27" target="_blank">2.5.2矩形的判定教案设计</a>,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明等内容,欢迎下载使用。
湘教版八年级下册2.5.2矩形的判定教案: 这是一份湘教版八年级下册<a href="/sx/tb_c95354_t8/?tag_id=27" target="_blank">2.5.2矩形的判定教案</a>,共9页。
初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定一等奖教案: 这是一份初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定一等奖教案,共4页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。













