
湘教版八年级下册4.2 一次函数优秀知识点教案
展开一次函数知识点总结
一、本节学习指导
本节的知识相当重要,同学们要引起重视,如果给出一个式子让其判断是不是一次函数,判断方法我们要掌握。关于一次函数的解析式的几种求法我们要会,特别是其中最常用的“待定系数法”。本节有配套免费学习视频。
二、知识要点
1.一次函数:形如y=kx+b (k≠0, k, b为常数)的函数。
注意:(1)要使y=kx+b是一次函数,必须k≠0。如果k=0,则kx=0,y=kx+b就不是一次函数;
(2)当b=0时,y=kx,y叫x的正比例函数。
2.图象:一次函数的图象是一条直线。【重点】
(1)两个常有的特殊点:与y轴交于(0,b);与x轴交于(-b/k,0)
(2)由图象可以知道,直线y=kx+b与直线y=kx平行,例如直线:y=2x+3与直线y=2x-5都与直线y=2x平行。
3.性质: 【重点】
(1)图象的位置:

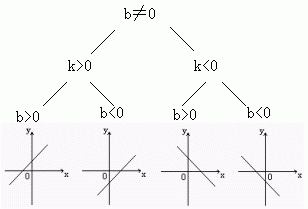
(2)增减性
k>0时,y随x增大而增大
k<0时,y随x增大而减小
4.求一次函数解析式的方法 【重点】
(1)由已知函数推导或推证
(2)由实际问题列出二元方程,再转化为函数解析式,此类题一般在没有写出函数解析式前无法(或不易)判断两个变量之间具有什么样的函数关系。
(3)用待定系数法求函数解析式。(最常用)
“待定系数法”的基本思想就是方程思想,就是把具有某种确定形式的数学问题,通过引入一些待定的系数,转化为方程(组)来解决,题目的已知恒等式中含有几个等待确定的系数,一般就需列出几个含有待定系数的方程,本单元构造方程一般有下列几种情况:
①利用一次函数的定义
x的系数不为0,x的最高次数为1,构造方程组。
②利用一次函数y=kx+b中常数项b恰为函数图象与y轴交点的纵坐标,即由b来定点;直线y=kx+b平行于y=kx,即由k来定方向 。
③利用函数图象上的点的横、纵坐标满足此函数解析式构造方程。
④利用题目已知条件直接构造方程 。
例:
(1)若函数是![]() 正比例函数,则k的值为( )
正比例函数,则k的值为( )
(2)已知![]() 是正比例函数,且y随x的增大而减小,则m的值为_______.
是正比例函数,且y随x的增大而减小,则m的值为_______.
(3)当m=_______时,函数![]() 是一次函数.
是一次函数.
解:
(1)由于y=(k+1)x+k²-1是正比例函数,
∴![]() ,∴k=1,∴应选B.
,∴k=1,∴应选B.
(2)![]() 是正比例函数的条件是:m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这两个条件得当
是正比例函数的条件是:m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这两个条件得当![]() 即m=-2时,
即m=-2时,![]() 是正比例函数且y随x的增大而减小.
是正比例函数且y随x的增大而减小.
(3)根据一次函数的定义可知,![]() 是一次函数的条件是:
是一次函数的条件是:
![]() 解得m=1或-3,故填1或-3.
解得m=1或-3,故填1或-3.
三、经验之谈:
1.判断一个式子是不是一次函数,首先看“k”是否等于零,其次看最高次项是否等于1次。
2.给出一个一次函数,我们要能迅速的画出图像,一看朝向,如果k>0,图像“向上爬”,k<0,图像“向下滑”;二看截距,截距就是|b|,如果b>0,图像和y轴的焦点在y的正半轴,如果b<0,则在y的负半轴。
3.一次函数的增减性很简单,当函数图像“向上爬”时,y随x的增大而增大;当函数图象“向下滑”时,y随x的增大而减小。
初中数学湘教版八年级下册4.4 用待定系数法确定一次函数表达式优秀教案及反思: 这是一份初中数学湘教版八年级下册4.4 用待定系数法确定一次函数表达式优秀教案及反思,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明等内容,欢迎下载使用。
湘教版八年级下册4.3 一次函数的图象优秀第2课时教案: 这是一份湘教版八年级下册4.3 一次函数的图象优秀第2课时教案,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明等内容,欢迎下载使用。
湘教版八年级下册4.5 一次函数的应用获奖第1课时教案及反思: 这是一份湘教版八年级下册4.5 一次函数的应用获奖第1课时教案及反思,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明等内容,欢迎下载使用。













