1.1 直角三角形的性质和判定（Ⅰ）（2课时）课件+教案+PPT练习＋素材

这是一份1.1 直角三角形的性质和判定（Ⅰ）（2课时）课件+教案+PPT练习＋素材

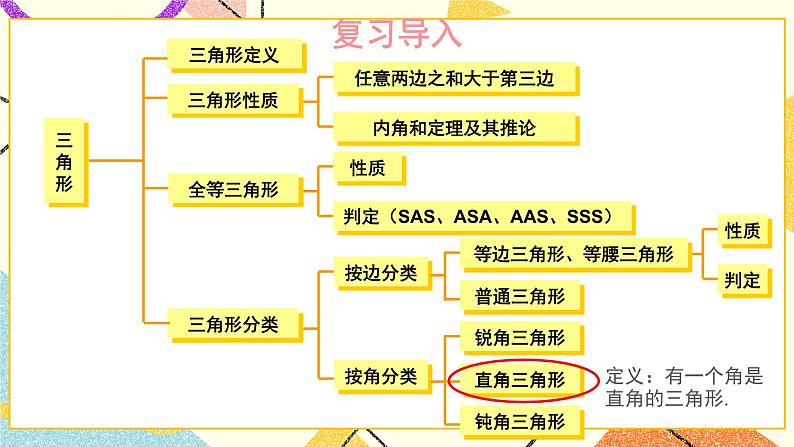
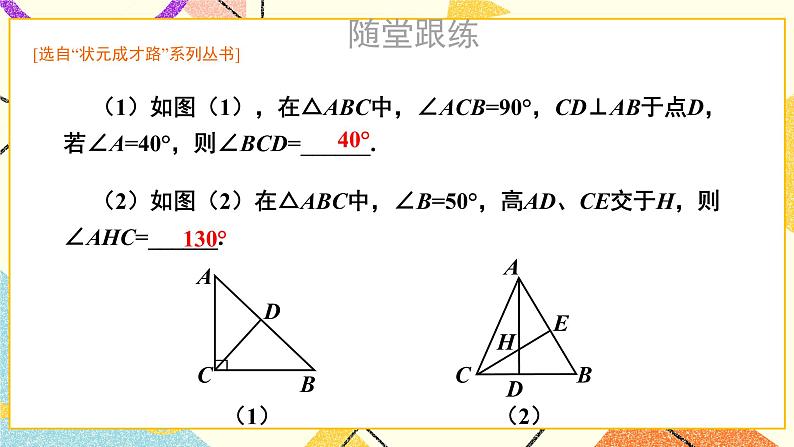
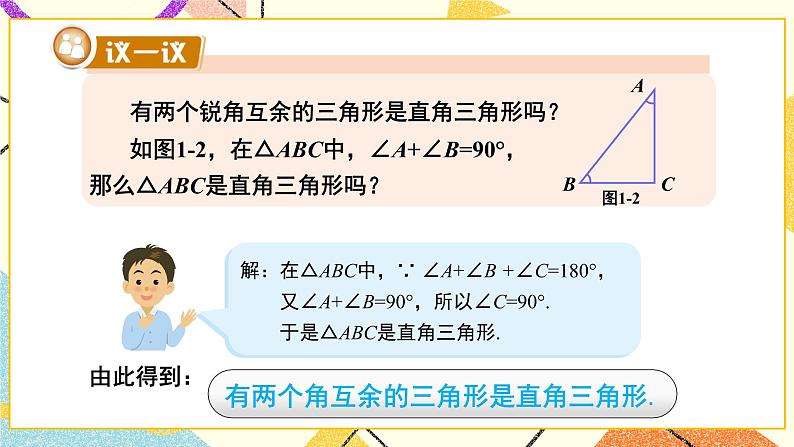
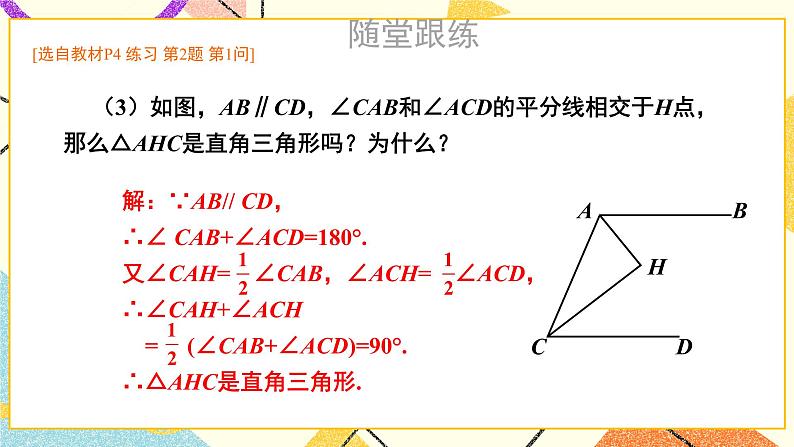
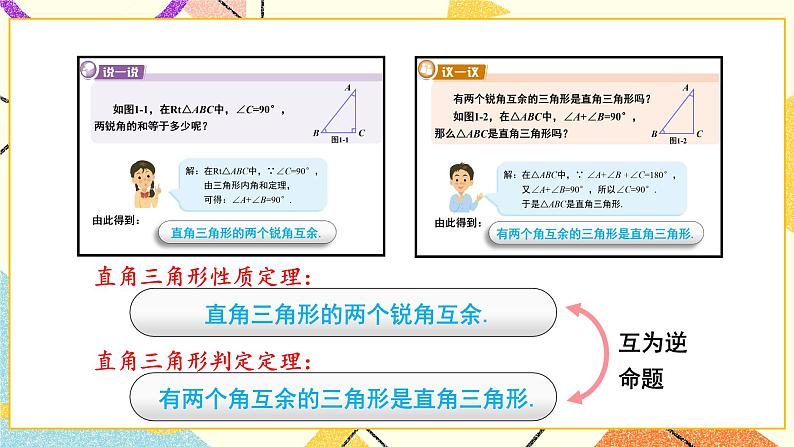
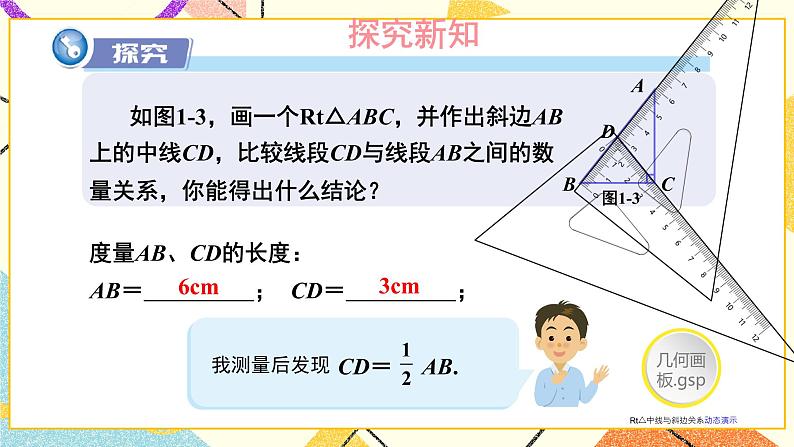
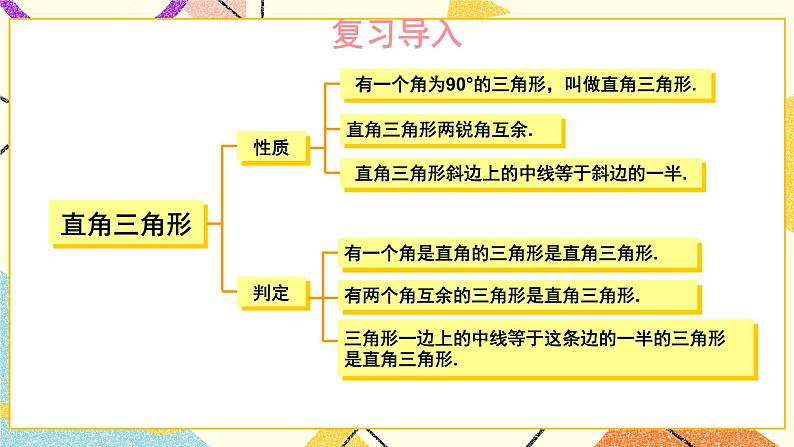
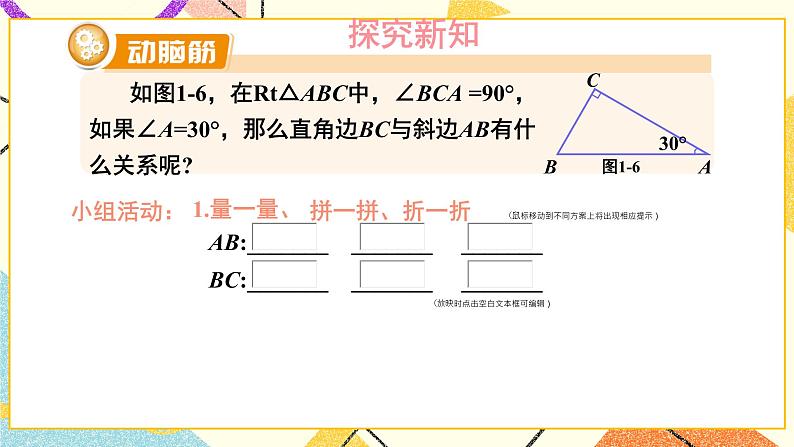
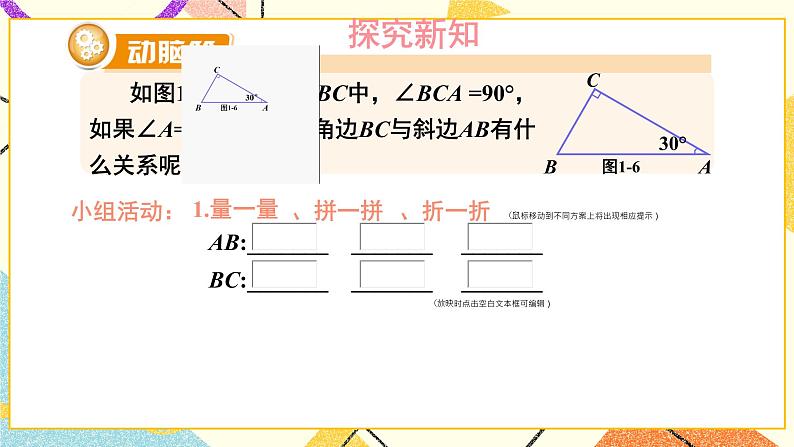
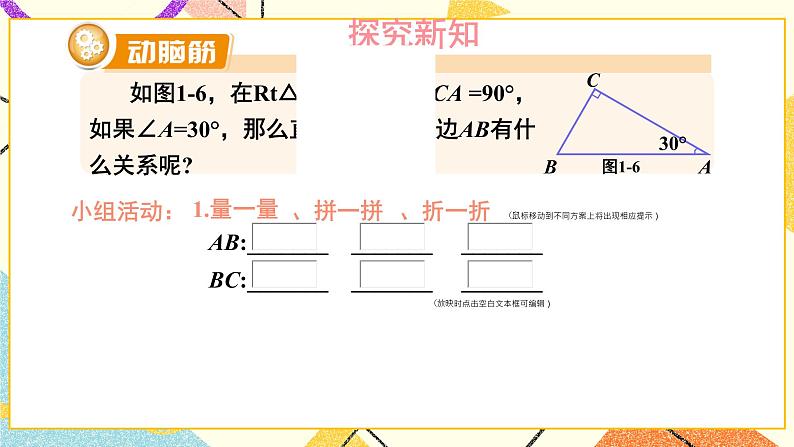
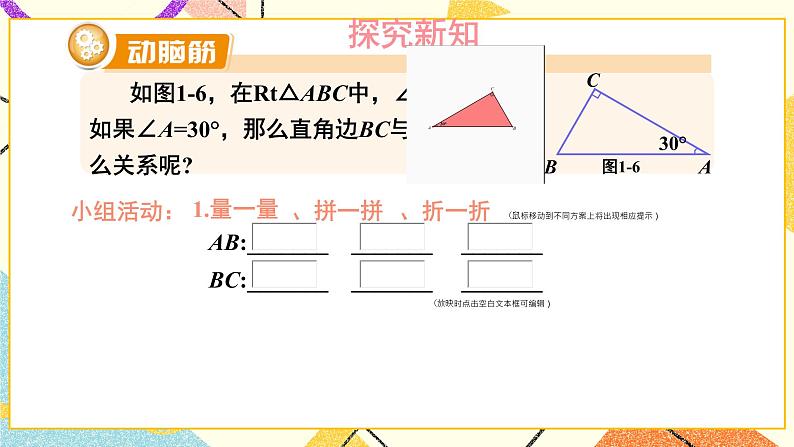
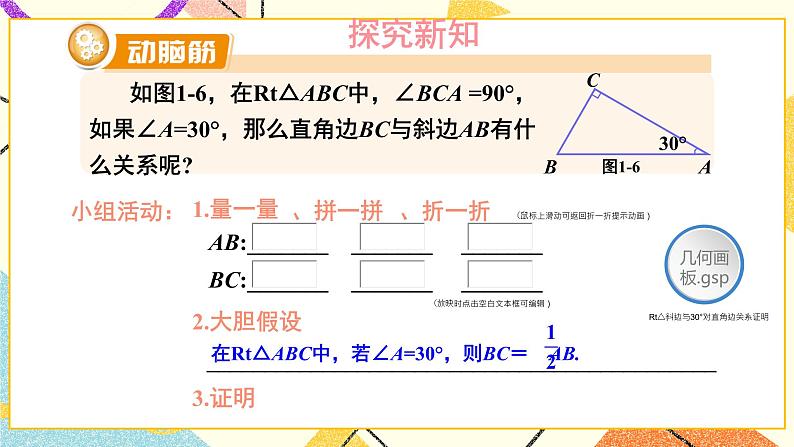
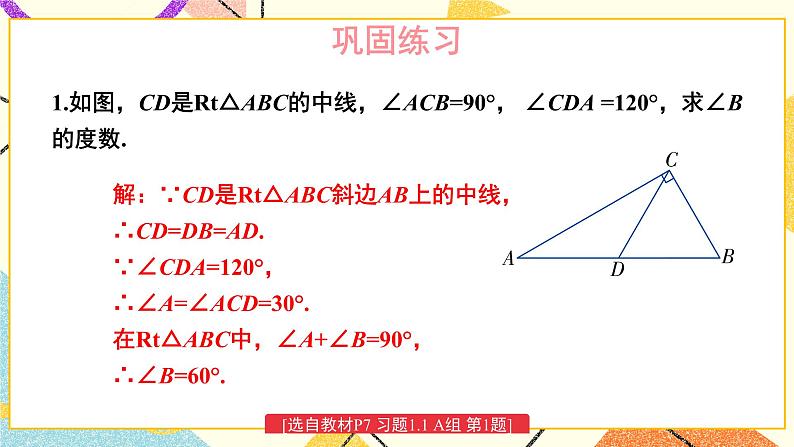
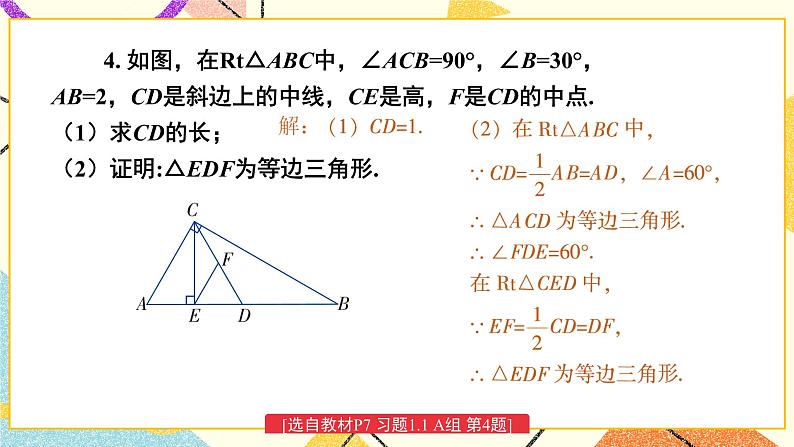
含30°角的直角三角形的性质及其应用湘教版·八年级数学下册①复习导入直角三角形新课引入 如图是某商店营业大厅电梯示意图.电梯AB的倾斜角为30°，大厅两层之间的高度BC为6 m.你能算出电梯AB的长度吗? 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?探究新知小组活动：1.量一量、AB:_______ _______ _______BC:_______ _______ _______（放映时点击空白文本框可编辑）拼一拼、折一折（鼠标移动到不同方案上将出现相应提示） 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?探究新知小组活动：1.量一量AB:_______ _______ _______BC:_______ _______ _______（放映时点击空白文本框可编辑）、拼一拼、折一折（鼠标移动到不同方案上将出现相应提示） 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?探究新知小组活动：1.量一量AB:_______ _______ _______BC:_______ _______ _______（放映时点击空白文本框可编辑）、拼一拼、折一折（鼠标移动到不同方案上将出现相应提示） 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?探究新知小组活动：1.量一量AB:_______ _______ _______BC:_______ _______ _______（放映时点击空白文本框可编辑）、拼一拼、折一折（鼠标移动到不同方案上将出现相应提示） 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?Rt△斜边与30°对直角边关系证明探究新知小组活动：1.量一量AB:_______ _______ _______BC:_______ _______ _______（放映时点击空白文本框可编辑）2.大胆假设____________________________________________3.证明、拼一拼、折一折（鼠标上滑动可返回折一折提示动画） 如图1-6，在Rt△ABC中，∠BCA =90°，如果∠A=30°，那么直角边BC与斜边AB有什么关系呢?探究新知证明：如图1-6，取线段AB的中点D，连接CD.∵CD是Rt△ABC斜边AB上的中线，∴CD= AB=BD.∵∠BCA =90°，且∠A =30°，∴∠B= 60°.∴△CBD为等边三角形，∴BC=BD= AB.于是，我们得到：探究新知例 2解: 如图1-7，取线段AB的中点D，连接CD.∵CD是Rt△ABC斜边AB上的中线,∴CD= AB=BD.∵BC= AB，∴BC= BD= CD，即△BDC为等边三角形.∴∠B= 60°.∵∠A+∠B=90°∴∠A=30°.由例2，你能得出什么结论？互为逆命题【教材P5】 如图1-8，在A岛周围20海里水域内有暗礁，一轮船由西向东航行到O处时，测得A岛在北偏东60°的方向，且与轮船相距 海里.若该船继续保持由西向东的航向，那么有触礁的危险吗?例 3探究新知1海里=1852mD图1-8【教材P5】巩固练习 1.如图是某商店营业大厅电梯示意图.电梯AB的倾斜角为30°，大厅两层之间的高度BC为6 m.你能算出电梯AB的长度吗?解：AB=2BC=2×6=12m[选自教材P6 练习 第1题]巩固练习 2.如图，在△ABC中，已知∠ACB=90°，CD垂直于AB，垂足为点D，∠A=30°.求证: AB=4BD.[选自教材P6 练习 第2题]巩固练习 1. 如图，线段AE与BC相交于点D，BD=CD， AD=ED， CA⊥AE，∠1=30°，且AB=3 cm.那么线段BE多长呢?[选自教材P7 习题1.1 A组 第3题]巩固练习 2. 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB=2，CD是斜边上的中线，CE是高，F是CD的中点.（1）求CD的长；（2）证明:△EDF为等边三角形.[选自教材P7 习题1.1 A组 第4题]巩固练习 3. 如图是某建筑物的屋顶架，其中AB=8m，D是AB的中点，BC，DE都垂直于AC.如果∠ABC= 60°，那么BC，DE，CD各是多少米?[选自教材P7 习题1.1 A组 第5题]巩固练习 4. 如图，在Rt△ABC中，∠C=90°，ED是线段AB的垂直平分线，已知∠1= ∠ABC，求∠A 的度数.[选自教材P8 习题1.1 B组 第6题]巩固练习 5. 将一副三角尺如图所示叠放在一起，若AB=14 cm，求阴影部分△ACF的面积.[选自教材P8 习题1.1 B组 第7题]巩固练习 6. 如图，小芳在山下发现正前方山上有个电视塔，测得塔尖的仰角为15°. 小芳朝正前方笔直行走400 m，此时测得塔尖的仰角为30°.若小芳的眼睛离地面1.6m，你能算出这个电视塔塔尖离地面的高度吗?[选自教材P8 习题1.1 B组 第8题]课堂小结在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°.直角三角形1.从课后习题中选取；2.完成练习册本课时的习题。课后作业