
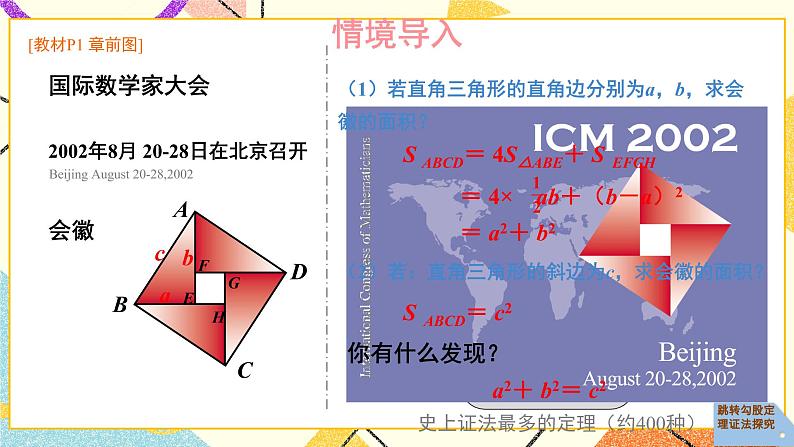
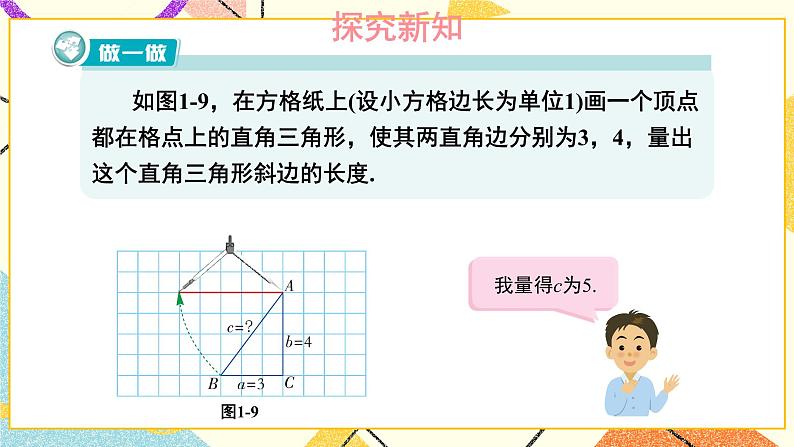
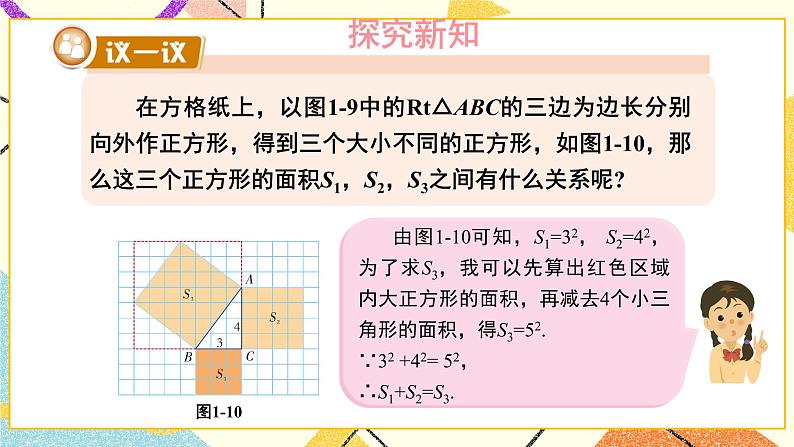

















1.2 直角三角形的性质和判定(Ⅱ)(3课时)课件+教案+PPT练习+素材
展开1.2 直角三角形的性质和判定(Ⅱ)
第3课时 勾股定理的逆定理
【知识与技能】
1.探索并掌握直角三角形判别的方法——勾股定理逆定理.
2.会应用勾股逆定理判别一个三角形是否是直角三角形.
3.通过三角形三边的数量关系来判断它是否为直角三角形,培养学生数形结合的思想.
【过程与方法】
通过“创设情境——实验验证——理论释意——应用”的探索过程,让学生感受知识的乐趣.
【情感态度】
1.通过合作交流学习的发展体验获取数学知识的感受.
2.通过对勾股定理逆定理的探究,激发学生学习数学的兴趣和创新精神.
【教学重点】
理解和应用直角三角形的判定方法.
【教学难点】
理解勾股定理的逆定理.
一、创设情境,导入新课
问题 据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
【教学说明】
利用古埃及人画直角的方法,让学生体验从实际问题中发现数学,同时明确了本节课所研究的问题,既进行了数学史的教育,又锻炼了学生观察探究的能力,激发了他们渴求知识的欲望,教师讲课前,先让学生完成预习.
二、思考探究,获取新知
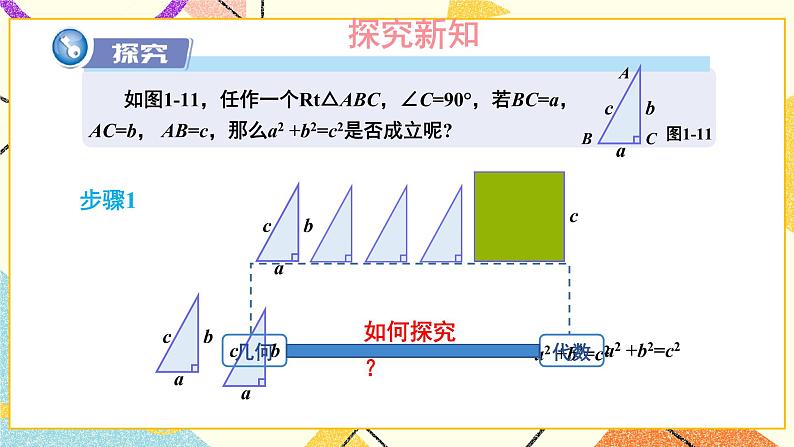
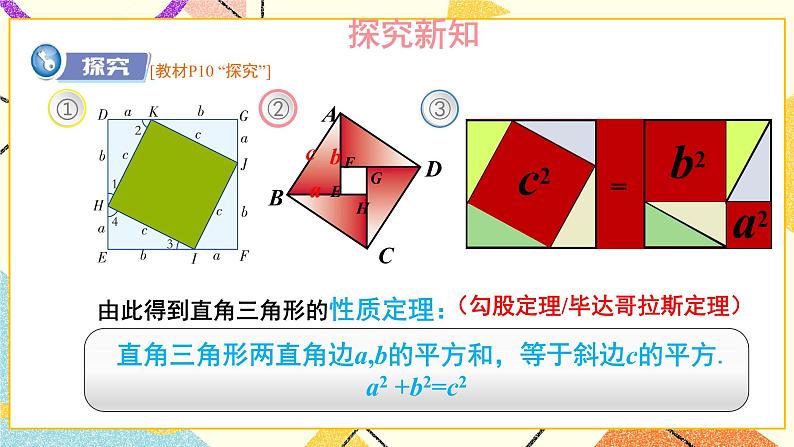
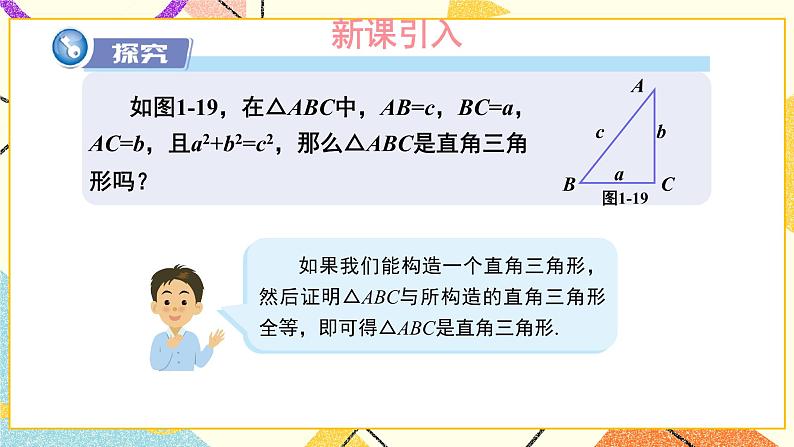
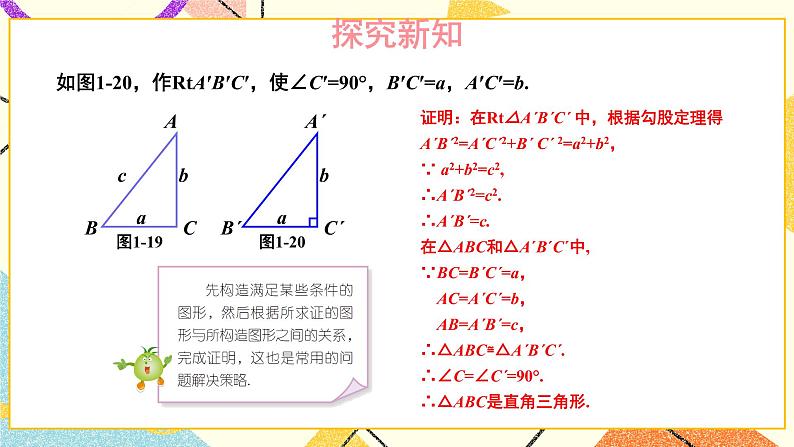
问题勾股定理的逆定理的证明探究教材第14页“探究”
【教学说明】
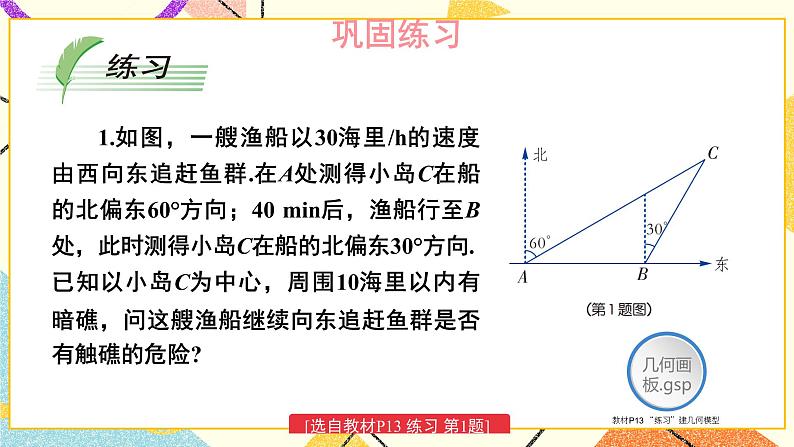
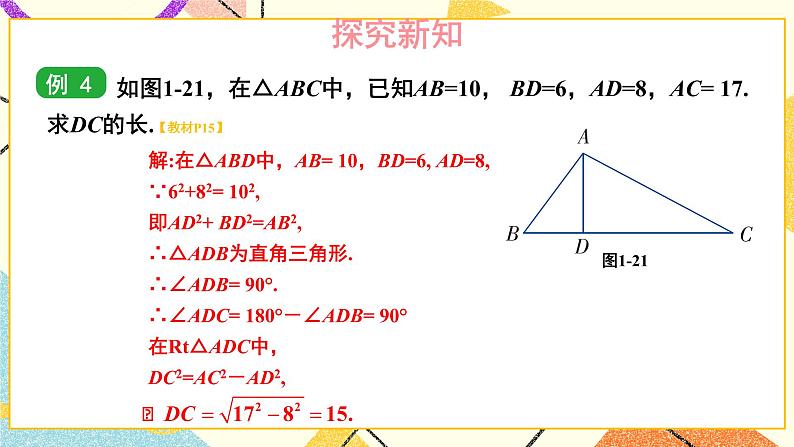
让学生有充分的探究、讨论的空间,体会逆定理的发生、发展、形成的过程,让学生亲身体验成功的喜悦,再次感受到数形结合的思想方法的应用.勾股定理的应用例:教材第15页例3、例4
【教学说明】
加深对勾股定理逆定理的理解,并能初步的应用逆定理.
三、运用新知,深化理解
1.下列命题中是假命题的是( )
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
D.△ABC中,若a∶b∶c=5∶4∶3,则△ABC是直角三角形
2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为__________,此三角形的形状为________.
3.若a、b、c是△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判定这个三角形的形状.
4.探险队里的A组由驻地出发,以12km/h的速度前进,同时,B组也由驻地出发,以9km/h的速度向另一个方向前进,2小时后同时停下来,这时A、B两组相距30km,那么A、B两组行驶的方向成直角吗?说明理由.
【教学说明】
由学生自主完成,考验学生学习过程中存在的问题,适时给予引导、点拨,并有针对性地加强训练.在完成上述题目后,让学生完成练习册中本课时 的对应训练部分.
答案:1. C 2. 6,8,10;直角三角形
3.∵a2c2-b2c2=a4-b4,∴c2(a2-b2)=(a2+b2)(a2-b2),当a2-b2=0时,即(a+b)(a-b)=0,因为a>0,b>0,所以a+b≠0,a-b=0,即a=b,此时为等腰三角形,当a2-b2≠0时,则有c2=a2+b2,根据勾股定理的逆定理此时为直角三角形.综上可得这个三角形的形状为等腰三角形或直角三角形.
4.∵(12×2)2+(9×2)2=30
∴A,B两组行驶方向成直角.
四、师生互动,课堂小结
通过学习,你能判断一个三角形是否为直角三角形吗?还有哪些困惑?请与同学们共同操作.
【教学说明】
引导学生回顾所学知识,加深理解,同学相互取长补短,共同提高.
1.布置作业:习题1.2中的第2、8题.
2.完成练习册中本课时 练习的作业部分.
学生在练习的过程中很容易受到固定思维模式的限制,往往不找最长边而总是按照先后顺序来解题,这样很容易发生错误,再就是利用勾股定理的逆定理进行有关的证明不是很得法.以后的教学中逐步训练提高.









