初中数学苏科版七年级上册2.6 有理数的乘法与除法优质ppt课件

这是一份初中数学苏科版七年级上册2.6 有理数的乘法与除法优质ppt课件，共60页。PPT课件主要包含了解3×26，×50，左边都有一个乘数3，解1原式，2原式，先确定积的符号，再确定积的绝对值，－28，－100，解法1等内容，欢迎下载使用。

2.6 有理数的乘法与除法
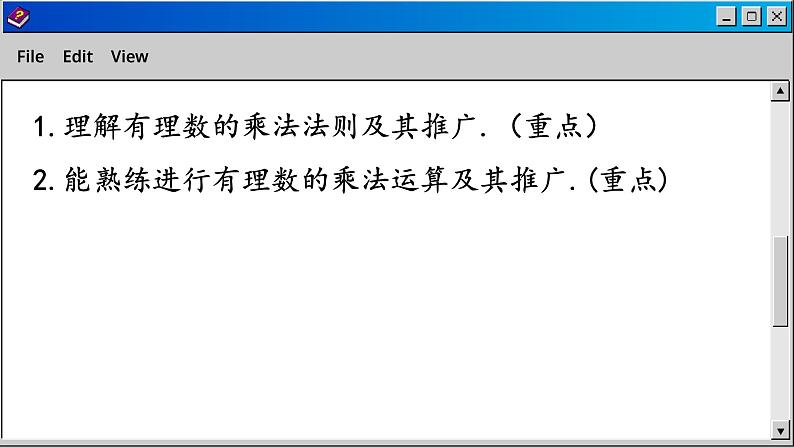
1.理解有理数的乘法法则及其推广.（重点）2.能熟练进行有理数的乘法运算及其推广.(重点)
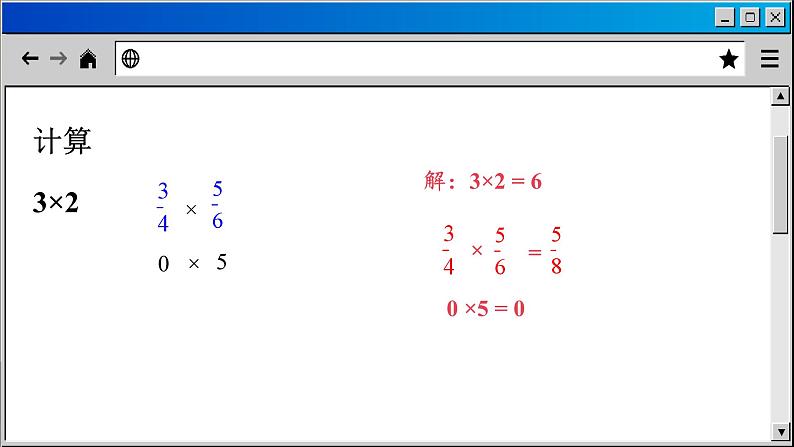
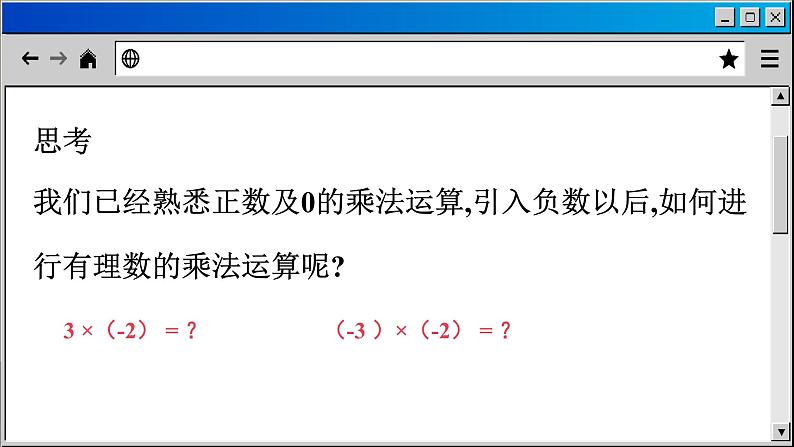
思考我们已经熟悉正数及0的乘法运算,引入负数以后,如何进行有理数的乘法运算呢?
3 ×（-2） = ？
（-3 ）×（-2） = ？
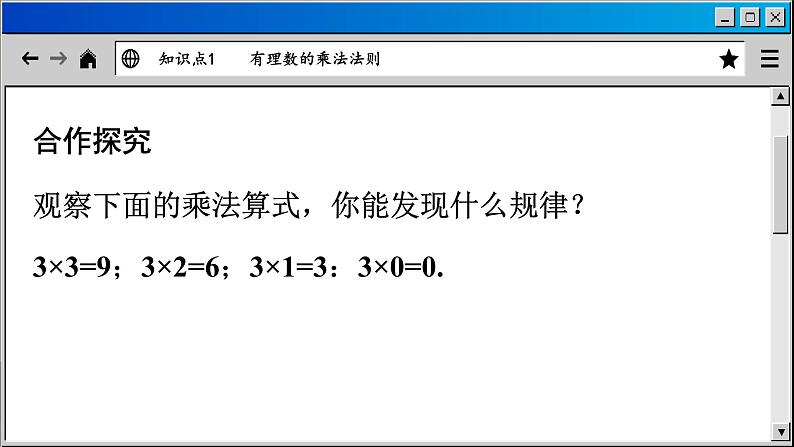
合作探究观察下面的乘法算式，你能发现什么规律？3×3=9；3×2=6；3×1=3：3×0=0.
知识点1 有理数的乘法法则
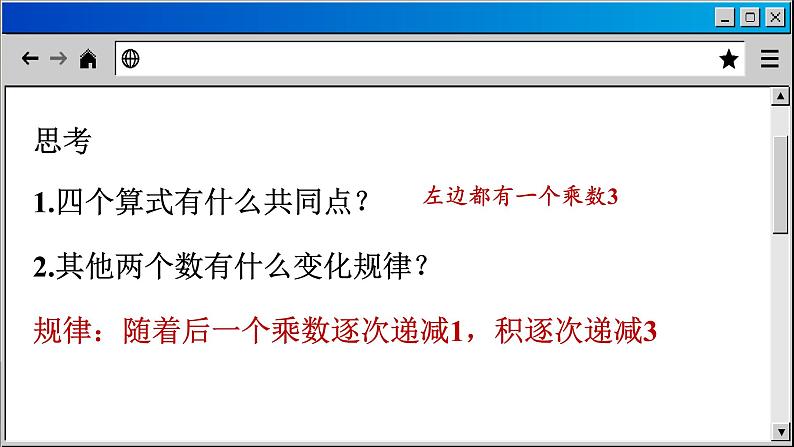
思考1.四个算式有什么共同点？2.其他两个数有什么变化规律？规律：随着后一个乘数逐次递减1，积逐次递减3
要使这个规律在引入负数后仍然成立，请完成下列算式。3×（-1）= -3；3×（-2）= ______3×（-3）= ____
观察下面的乘法算式，你又能发现什么规律？3×3=9；2×3=6；1×3=3；0×3=0.结论 类比上一过程，我们可以得出下面规律： 随着前一个乘数逐次递减1，积逐次递减3
要使这个规律在引入负数后仍然成立，请完成下列算式（-1）×3= ；（-2）×3= ；（-3）×3= ；
3×（-1）=-3；3×（-2）=-6；3×（-3）=-9；
从符号和绝对值两个角度观察这四组算式，你能得出什么结论？
正数乘正数，积为正数；正数乘负数，积是负数；负数乘正数，积也是负数。积的绝对值等于各乘数绝对值的积。0乘正数或负数，积都是0
根据上面得出的结论计算下面的算式，你发现有什么规律？（-3）×3=_______（-3）×2=_______（-3）×1=________（-3）×0=_______规律:随着后一个乘数逐次递减1，积逐次增加3
根据上面得出的规律计算下面的算式，你从中可以归纳出什么结论？（-3）×（-1）= ；（-3）×（-2）= ；（-3）×（-3）= ；
结论：负数乘负数，积为正数,乘积的绝对值等于各乘数绝对值的积.
结论有理数乘法法则两数相乘，同号得正，异号得负，并把绝对值相乘.任何数与0相乘，都得0.
1. 计算 （1）（-5） ×（-3） （2） （-7）×4
计算(1)3×4 (2) (−3)×9
解： (1) 3×4 (2) (−3)×9 = +(3×4) = −(3×9) = 12 . = − 27.
(3)8 ×（-1） (4)（-3）×（-4）
(3) 8×（-1） (4)（-3）×（-4） = −（8 ×1） = +（3×4） = −8. = 12.
有理数乘法的求解步骤：(1)确定积的符号;(2)把绝对值相乘.
观察下列各式，它们的积是正的还是负的？
知识点2 有理数乘法法则的推广
思考：几个不是0的数相乘，积的符号与负因数的个数之间有什么关系？
结论几个不是0的数相乘，负因数的个数是______时，积是正数；负因数的个数是______时，积是负数．
多个不是0的数相乘，先做哪一步，再做哪一步？先定符号，再算绝对值.
你能看出下式的结果吗？如果能，请说明理由．
结论几个数相乘，如果其中有因数为0，积等于____．
2．(河北中考) 计算3×(-2) 的结果是（ ）(A)5 (B)-5 (C)6 (D)-63（宜昌中考）如果ab<0，那么下列判断正确的是( )(A)a<0，b<0 (B)a>0，b>0 (C)a≥0，b≤0 (D)a<0，b>0或a>0，b<0
分析:同号得正，异号得负.
4.计算：
解：（1）原式=(-6)×(-4)= 24
若a、b、c为有理数，且|a+1|+|b+2|+|c+3|=0，求(a-1)(b+2)(c-3)的值.解：∵ |a+1|+|b+2|+|c+3|=0， ∴ a=-1，b=-2，c=-3, 则(a-1)(b+2)(c-3)=0.
课时2 有理数的乘法运算律
1.掌握有理数乘法的运算律，并利用运算律简化乘法运算; (重点)2.掌握乘法的分配律，并能灵活的运用.(难点)
1.有理数的乘法法则是什么？两数相乘，同号得正，异号得负，并把绝对值相乘.任何数与0相乘，都得0. 2.进行多个有理数的乘法运算的一般步骤（1）定号（奇负偶正）. （2）算值（积的绝对值）.
3.小学阶段我们学过乘法的哪些运算律？乘法交换律、乘法结合律、乘法分配律.
计算下列各式(1)5×（-6）＝ （-6）×5＝(2)[3×(-4)]×5＝ 3×[(-4)×5]＝ (3)2×[3＋(-4)]＝ 2×3＋2×(-4)＝
5×（-6） （-6）×5
[3×(-4)]× 5 3×[(-4)×5]
2×[3＋(-4)] 2×3＋2×(-4)
知识点1 有理数的乘法运算律
每小组运算分别体现了什么运算律？(1)5×（-6）＝ （-6）×5＝(2)[3×(-4)]×5＝ 3×[(-4)×5]＝ (3)2×[3＋(-4)]＝ 2×3＋2×(-4)＝
1.乘法交换律:两个数相乘,交换因数的位置,积相等.2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
3.乘法分配律：一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
a(b＋c）=ab＋ac
根据乘法交换律和结合律可以推出：三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.根据分配律可以推出：一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
1.计算：（－4）×15×（－25）解：原式=15×（－4）×（－25）=15×［（－25）×（－4）］=15×100=1500
(1) (-85)×(-25)×(-4)
计算：(1) (2)观察两式有什么特点？乘积是1的两个数互为倒数．
知识点2 倒数
互为倒数与互为相反数的区别：
1.下列各式变形各用了哪些运算律？(1) 1.25×(-4)×(-25)×8=(1.25×8)×[(-4)×(-25)]
（乘法交换律和结合律）
（加法结合律和乘法分配律）
（乘法交换律和加法交换律）
2.下列计算(-55)×99+(-44)×99-99正确的是( )A.原式=99×(-55-44)=-9801 B.原式=99×(-55-44+1)=-9702C.原式=99×(-55-44-1)=-9900 D.原式=99×(-55-44-99)=-19602
3.若a、b互为相反数，若x、y互为倒数，则a-xy +b= .4.相反数等于它本身的数是 ；倒数等于它本身的数是 ；绝对值等于它本身的数是 .
利用分配律可以得到-2×6＋3×6=（-2＋3）×6，如果用a表示任意一个数，那么利用分配律可以得到-2a＋3a等于什么？类似地：2ab-5ab又等于什么呢？解：-2a+3a=(-2+3)a; 2ab-5ab=(2-5)ab.
1.能表述出有理数除法法则;（重点）2．会运用法则进行有理数乘除混合运算.（重点、难点）
1.什么是倒数？2.你能很快地说出下列各数的倒数吗?
正数除以负数 8÷(－4)负数除以负数 (－8)÷(－4)零除以负数 0÷(－4)
知识点1 有理数的除法法则
结论除以一个负数等于乘以这个负数的倒数。有理数除法法则除以一个不等于0的数，等于乘这个数的倒数用字母表示为
结论两个不等于0的数相除，同号得正，异号得负，并把绝对值相除.0除以任何一个不等于0的数，都得0.
（-36）÷ 9= -(36÷9)=-4；
2 化简下列各式：
(－36)÷9＝－(36÷9)＝－4
知识点2 有理数的乘除混合运算
有理数乘除法混合运算的步骤:(1)将所有的除法转化为乘法.(2)先确定积的符号，再把绝对值相乘.(3)运用乘法运算律，简化运算.(4)求出最后的结果.
1.已知(-2)×(-3)=6，则6÷(-2)= _______，6÷(-3)=______.2.下列运算结果等于1的是( )A.(-3)+(-3) B.(-3)-(-3)C.(-3)×(-3) D.(-3)÷(-3)
计算：(-4)÷2=____ 4÷(-2)=___ (-4)÷(-2)=___联系这类具体的数的除法，你认为下列式子是否成立(a、b是有理数，b≠0)？从它们可以总结什么规律？
乘法法则:两个数相乘,同号得正,异号得负,并把绝对值相乘;0与任何数相乘都为0.
(ab)c ＝ a(bc)
a(b＋c)=ab+ac
法则1:除以一个不等于0的数，等于乘这个数的倒数.
法则2:两个不等于0的数相除，同号得正，异号得负，并把绝对值相除.0除以任何一个不等于0的数，都得0.