北师大版七年级下册3 探索三角形全等的条件课时练习

这是一份北师大版七年级下册3 探索三角形全等的条件课时练习，共12页。试卷主要包含了下列图形具有稳定性的是等内容，欢迎下载使用。

1．下列图形具有稳定性的是（ ）
A．正方形B．矩形C．平行四边形D．直角三角形
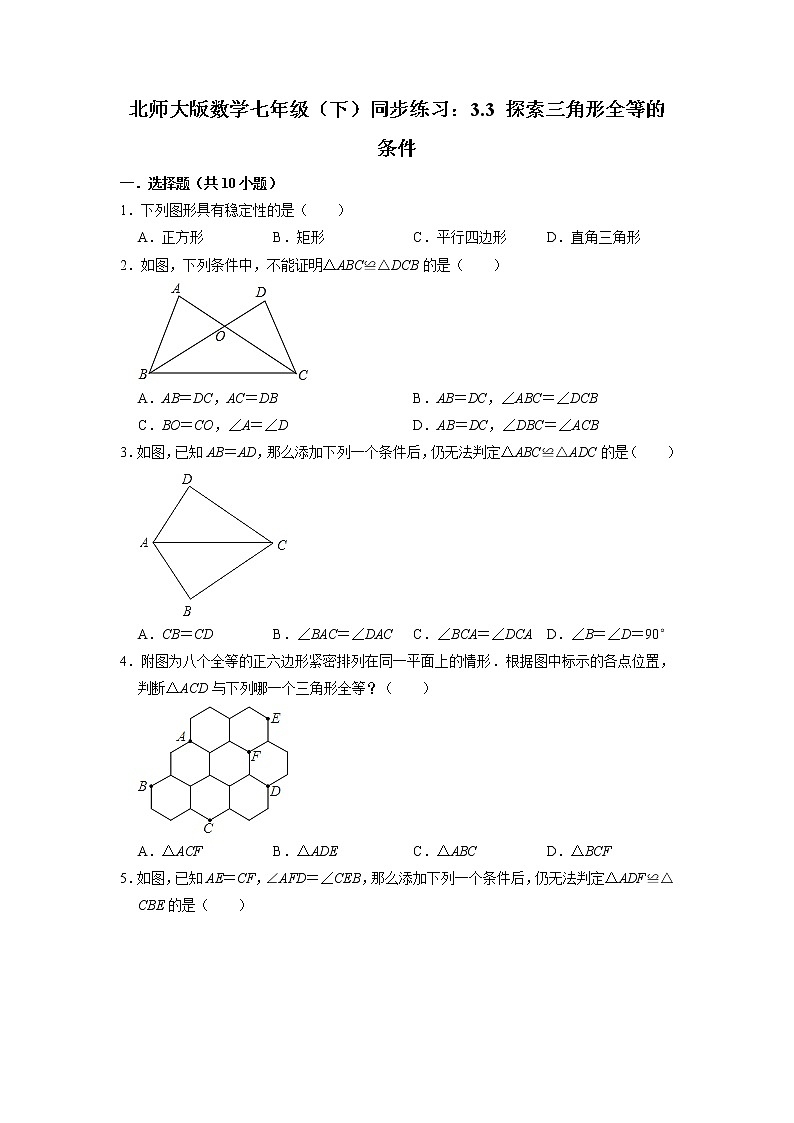
2．如图，下列条件中，不能证明△ABC≌△DCB的是（ ）
A．AB＝DC，AC＝DBB．AB＝DC，∠ABC＝∠DCB
C．BO＝CO，∠A＝∠DD．AB＝DC，∠DBC＝∠ACB
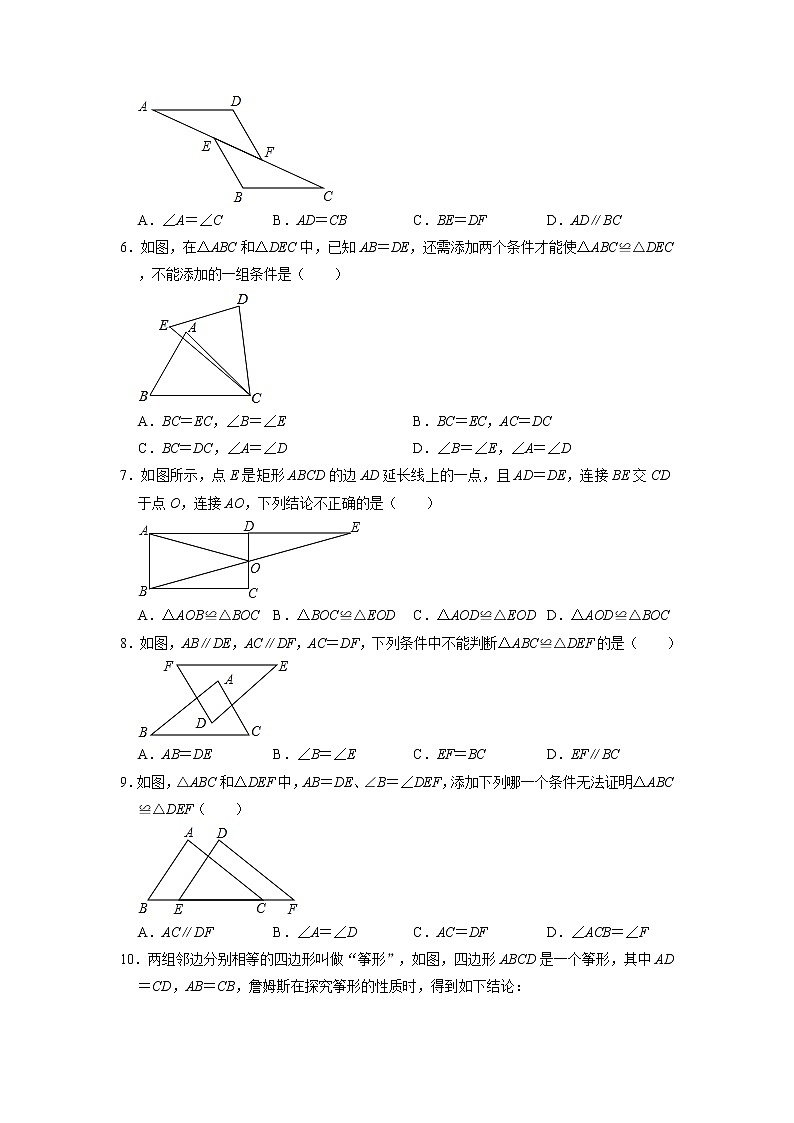
3．如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A．CB＝CDB．∠BAC＝∠DACC．∠BCA＝∠DCAD．∠B＝∠D＝90°
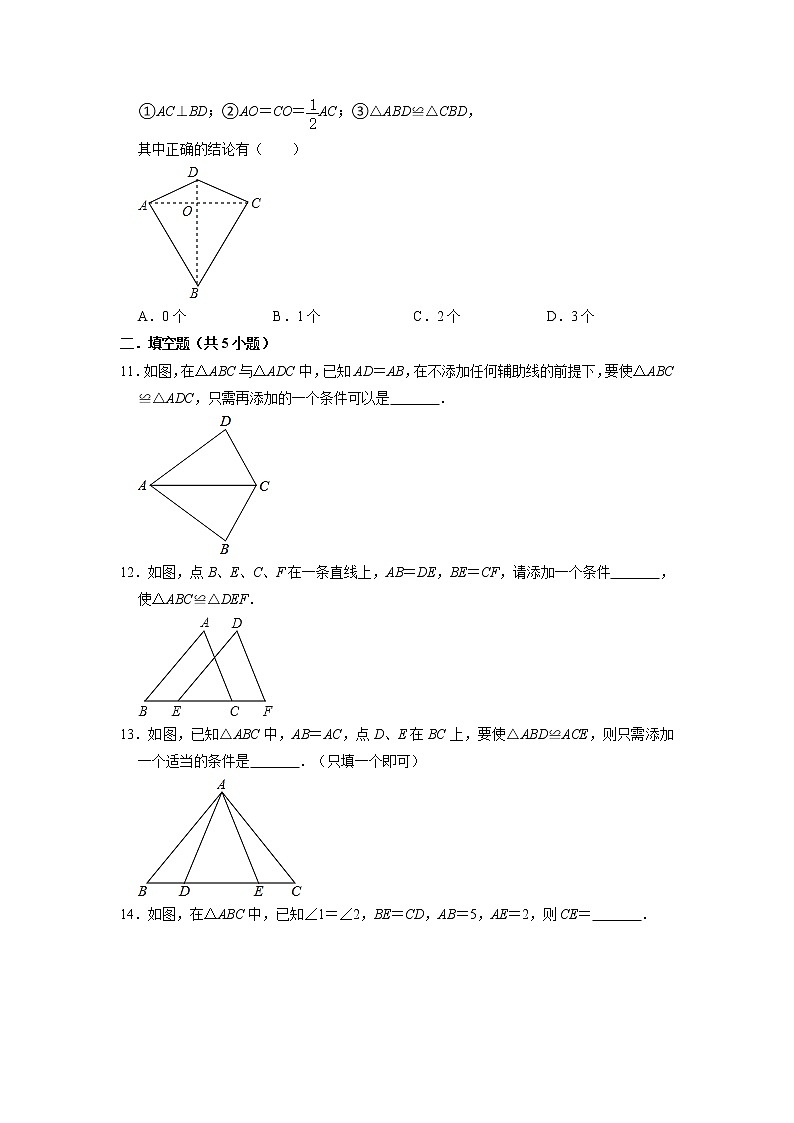
4．附图为八个全等的正六边形紧密排列在同一平面上的情形．根据图中标示的各点位置，判断△ACD与下列哪一个三角形全等？（ ）
A．△ACFB．△ADEC．△ABCD．△BCF
5．如图，已知AE＝CF，∠AFD＝∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）
A．∠A＝∠CB．AD＝CBC．BE＝DFD．AD∥BC
6．如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（ ）
A．BC＝EC，∠B＝∠EB．BC＝EC，AC＝DC
C．BC＝DC，∠A＝∠DD．∠B＝∠E，∠A＝∠D
7．如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD＝DE，连接BE交CD于点O，连接AO，下列结论不正确的是（ ）
A．△AOB≌△BOCB．△BOC≌△EODC．△AOD≌△EODD．△AOD≌△BOC
8．如图，AB∥DE，AC∥DF，AC＝DF，下列条件中不能判断△ABC≌△DEF的是（ ）
A．AB＝DEB．∠B＝∠EC．EF＝BCD．EF∥BC
9．如图，△ABC和△DEF中，AB＝DE、∠B＝∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）
A．AC∥DFB．∠A＝∠DC．AC＝DFD．∠ACB＝∠F
10．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB，詹姆斯在探究筝形的性质时，得到如下结论：
①AC⊥BD；②AO＝CO＝AC；③△ABD≌△CBD，
其中正确的结论有（ ）
A．0个B．1个C．2个D．3个
二．填空题（共5小题）
11．如图，在△ABC与△ADC中，已知AD＝AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是 ．
12．如图，点B、E、C、F在一条直线上，AB＝DE，BE＝CF，请添加一个条件 ，使△ABC≌△DEF．
13．如图，已知△ABC中，AB＝AC，点D、E在BC上，要使△ABD≌ACE，则只需添加一个适当的条件是 ．（只填一个即可）
14．如图，在△ABC中，已知∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝ ．
15．如图，A，B，C三点在同一条直线上，∠A＝∠C＝90°，AB＝CD，请添加一个适当的条件 ，使得△EAB≌△BCD．
三．解答题（共5小题）
16．如图，四边形ABCD中，E点在AD上，其中∠BAE＝∠BCE＝∠ACD＝90°，且BC＝CE，求证：△ABC与△DEC全等．
17．如图，∠B＝∠D，请添加一个条件（不得添加辅助线），使得△ABC≌△ADC，并说明理由．
18．已知：如图，点C为AB中点，CD＝BE，CD∥BE．
求证：△ACD≌△CBE．
19．如图，点C，F在线段BE上，BF＝EC，∠1＝∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）
20．如图，在△ABC中，AB＝AC，BD＝CD，DE⊥AB，DF⊥AC，垂足分别为点E、F．
求证：△BED≌△CFD．
北师大版数学七年级（下）同步练习：3.3 探索三角形全等的条件
参考答案与试题解析
一．选择题（共10小题）
1． 解：直角三角形具有稳定性．
故选：D．
2． 解：根据题意知，BC边为公共边．
A、由“SSS”可以判定△ABC≌△DCB，故本选项错误；
B、由“SAS”可以判定△ABC≌△DCB，故本选项错误；
C、由BO＝CO可以推知∠ACB＝∠DBC，则由“AAS”可以判定△ABC≌△DCB，故本选项错误；
D、由“SSA”不能判定△ABC≌△DCB，故本选项正确．
故选：D．
3． 解：A、添加CB＝CD，根据SSS，能判定△ABC≌△ADC，故A选项不符合题意；
B、添加∠BAC＝∠DAC，根据SAS，能判定△ABC≌△ADC，故B选项不符合题意；
C、添加∠BCA＝∠DCA时，不能判定△ABC≌△ADC，故C选项符合题意；
D、添加∠B＝∠D＝90°，根据HL，能判定△ABC≌△ADC，故D选项不符合题意；
故选：C．
4． 解：根据图象可知△ACD和△ADE全等，
理由是：∵根据图形可知AD＝AD，AE＝AC，DE＝DC，
∴△ACD≌△AED，
即△ACD和△ADE全等，
故选：B．
5． 解：∵AE＝CF，
∴AE+EF＝CF+EF，
∴AF＝CE，
A、∵在△ADF和△CBE中
∴△ADF≌△CBE（ASA），正确，故本选项错误；
B、根据AD＝CB，AF＝CE，∠AFD＝∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；
C、∵在△ADF和△CBE中
∴△ADF≌△CBE（SAS），正确，故本选项错误；
D、∵AD∥BC，
∴∠A＝∠C，
∵在△ADF和△CBE中
∴△ADF≌△CBE（ASA），正确，故本选项错误；
故选：B．
6． 解：A、已知AB＝DE，再加上条件BC＝EC，∠B＝∠E可利用SAS证明△ABC≌△DEC，故此选项不合题意；
B、已知AB＝DE，再加上条件BC＝EC，AC＝DC可利用SSS证明△ABC≌△DEC，故此选项不合题意；
C、已知AB＝DE，再加上条件BC＝DC，∠A＝∠D不能证明△ABC≌△DEC，故此选项符合题意；
D、已知AB＝DE，再加上条件∠B＝∠E，∠A＝∠D可利用ASA证明△ABC≌△DEC，故此选项不合题意；
故选：C．
7． 解：∵AD＝DE，DO∥AB，
∴OD为△ABE的中位线，
∴OD＝OC，
∵在△AOD和△EOD中，
，
∴△AOD≌△EOD（SAS）；
∵在△AOD和△BOC中，
，
∴△AOD≌△BOC（SAS）；
∵△AOD≌△EOD，
∴△BOC≌△EOD；
故B、C、D均正确．
故选：A．
8． 解：∵AB∥DE，AC∥DF，∴∠A＝∠D，
（1）AB＝DE，则△ABC和△DEF中，，∴△ABC≌△DEF，故A选项错误；
（2）∠B＝∠E，则△ABC和△DEF中，，∴△ABC≌△DEF，故B选项错误；
（3）EF＝BC，无法证明△ABC≌△DEF（ASS）；故C选项正确；
（4）∵EF∥BC，AB∥DE，∴∠B＝∠E，则△ABC和△DEF中，，∴△ABC≌△DEF，故D选项错误；
故选：C．
9． 解：∵AB＝DE，∠B＝∠DEF，
∴添加AC∥DF，得出∠ACB＝∠F，即可证明△ABC≌△DEF，故A、D都正确；
当添加∠A＝∠D时，根据ASA，也可证明△ABC≌△DEF，故B正确；
但添加AC＝DF时，没有SSA定理，不能证明△ABC≌△DEF，故C不正确；
故选：C．
10． 解：在△ABD与△CBD中，
，
∴△ABD≌△CBD（SSS），
故③正确；
∴∠ADB＝∠CDB，
在△AOD与△COD中，
，
∴△AOD≌△COD（SAS），
∴∠AOD＝∠COD＝90°，AO＝OC，
∴AC⊥DB，
故①②正确；
故选：D．
二．填空题（共5小题）
11． 解：添加条件为DC＝BC，
在△ABC和△ADC中，
，
∴△ABC≌△ADC（SSS）；
若添加条件为∠DAC＝∠BAC，
在△ABC和△ADC中，
，
∴△ABC≌△ADC（SAS）．
故答案为：DC＝BC或∠DAC＝∠BAC
12． 解：①添加AC＝DF．
∵BE＝CF，
∴BC＝EF，
∵在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS）．
②添加∠B＝∠DEF．
∵BE＝CF，
∴BC＝EF，
∵在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS）．
③添加AB∥DE．
∵BE＝CF，
∴BC＝EF，
∵AB∥DE，
∴∠B＝∠DEF，
∵在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS）．
故答案为：AC＝DF（或∠B＝∠DEF或AB∥DE）．
13． 解：BD＝CE，
理由是：∵AB＝AC，
∴∠B＝∠C，
在△ABD和△ACE中，，
∴△ABD≌△ACE（SAS），
故答案为：BD＝CE．
14． 解：△ABE和△ACD中，
，
∴△ABE≌△ACD（AAS），
∴AD＝AE＝2，AC＝AB＝5，
∴CE＝BD＝AB﹣AD＝3，
故答案为3．
15． 解：∵∠A＝∠C＝90°，AB＝CD，
∴若利用“SAS”，可添加AE＝CB，
若利用“HL”，可添加EB＝BD，
若利用“ASA”或“AAS”，可添加∠EBD＝90°，
若添加∠E＝∠DBC，可利用“AAS”证明．
综上所述，可添加的条件为AE＝CB（或EB＝BD或∠EBD＝90°或∠E＝∠DBC等）．
故答案为：AE＝CB．
三．解答题（共5小题）
16． 解：∵∠BCE＝∠ACD＝90°，
∴∠3+∠4＝∠4+∠5，
∴∠3＝∠5，
在△ACD中，∠ACD＝90°，
∴∠2+∠D＝90°，
∵∠BAE＝∠1+∠2＝90°，
∴∠1＝∠D，
在△ABC和△DEC中，
，
∴△ABC≌△DEC（AAS）．
17． 解：添加∠BAC＝∠DAC．理由如下：
在△ABC与△ADC中，
，
∴△ABC≌△ADC（AAS）．
18． 证明：∵C是AB的中点（已知），
∴AC＝CB（线段中点的定义）．
∵CD∥BE（已知），
∴∠ACD＝∠B（两直线平行，同位角相等）．
在△ACD和△CBE中，
，
∴△ACD≌△CBE（SAS）．
19． AC＝DF．
证明：∵BF＝EC，
∴BF﹣CF＝EC﹣CF，
∴BC＝EF，
在△ABC和△DEF中
∴△ABC≌△DEF（SAS）．
20． 证明：∵DE⊥AB，DF⊥AC，
∴∠BED＝∠CFD＝90°，
∵AB＝AC，
∴∠B＝∠C，
在△BED和△CFD中，
，
∴△BED≌△CFD（AAS）．