





数学八年级上册4.1 平方根教学ppt课件
展开平方根的定义平方根的性质 求平方根(开平方) 与 的性质
想一想(1)9的算术平方根是3,也就是说,3的平方是9. 还有其他的数,它的平方也是9吗?(2)平方等于 的数有几个?平方等于0.64的 数呢?
一般地,如果一个数x的平方等于a,即x2 = a,那么这个数x就叫做a的平方根(也叫做二 次方根) .如:±3是9的平方根, 或说成9的平方根是±3.
方法点拨:求一个正数的平方根的方法: 先找出平方等于这个正数的数,这样的数有两个,它们互为相反数,因而这两个数均为这个正数的平方根. 如果一个数为带分数,一般先将其化为假分数,再求平方根;如果有平方运算,那么先用平方运算求出结果,针对结果再求平方根;如果这个正数a 不能写成有理数的平方的形式,那么可以将a 的平方根表示成±
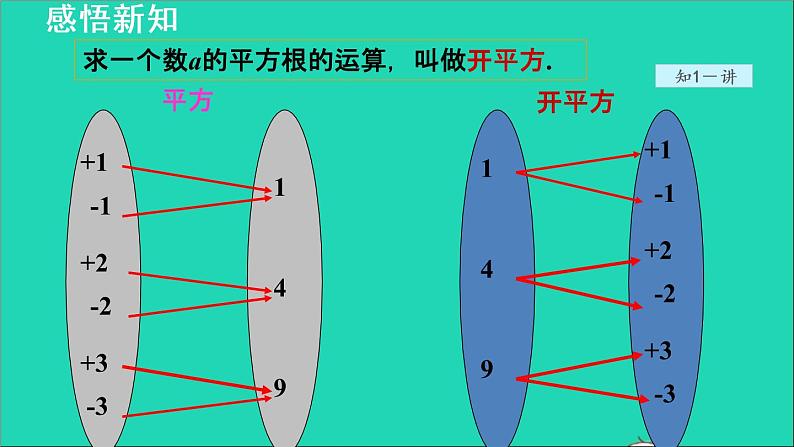
求一个数a的平方根的运算,叫做开平方.
下列说法中正确的是( )A.9的平方根是±3,应表示为92=±3B.±3是9的平方根,应表示为± =3C.9开平方能得到9的平方根,即 =±3D.9的算术平方根是3,应表示为 =3
正确把握并准确运用平方根、算术平方根的定义.
必须弄清以下符号的意义:± (a≥0)表示非负数a的平方根, (a≥0)表示非负数a的算术平方根,把非负数a开平方,它的平方根可用± 表示.
平方根概念的起源与几何中的正方形有关. 如果一个正方形的面积为A,那么 这个正方形的边长是多少?.
正方形的面积是边长的平方,根据算术平方根的定义可得:正方形的边长是 (A>0).
议一议 (1)一个正数有几个平方根? (2)0有几个平方根? (3)负数呢?
平方根的性质(1)平方根的性质: 一个正数有两个平方根;0只有一个平方 根,它是0本身;负数没有平方根. (2)平方根的表示方法: 正数a有两个平方根,一个是a的算术平 方根 ,另一个是 ,它们互为相反 数.这两个平方根合起来可以记作 读作“正、负根号a”.
求下列各式的值:(1) ;(2) ; (3) .
(1)因为62=36,所以 =6; (2)因为0.92=0.81,所以 ;(3)因为 ,所以 .
求一个式子的值,先分析式子的意义,特别是看清它表示的是算术平方根还是平方根,就是看清符号,最后的结果不改变它的正负性.
判断下列说法是否正确:(1) 0的平方根是0;(2) 1的平方根是1;(3) -1的平方根是-1;(4) 0.01是0.1的一个平方根.
(1)正确;(2)错误;(3)错误;(4)错误.
下列说法正确的有( )①-2是-4的一个平方根;②a2的平方根是a;③2是4的一个平方根;④4的平方根是-2.A.1个 B.2个 C.3个 D.4个
1.开平方: 求一个数a的平方根的运算,叫做开平方, a叫做被开方数.2.要点精析: (1)一个正数的正的平方根就是它的算术平方根. (2)平方与开平方是互逆运算.开平方与加、减、乘、 除、乘方一样是一种运算,即: 运算名称:加、减、乘、除、乘方、开平方(非负数). 运算结果:和、差、积、商、幂、平方根(互为相反数).
求下列各数的平方根:(1) 100; (2) ; (3) 0.25.
(1)因为(±10)2=100,所以100的平方根是±10;(2)因为 ,所以 的平方根是(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
要从根本之处理解一个数的平方根的运算,从平方根的概念入手,同时要知道,只有非负数才有平方根.同时注意平方根的通用符号是 (a≥0),防止粗心大意漏掉“ ”而出错.
计算下列各式的值: (1) ; (2) ; (3) .
(3)因为 ,所以 .
与 的性质
1.想一想: (1) 等于多少? 等于多少? (2) 等于多少? (3)对于正数a, 等于多少?2.联系拓广: 对于任意数a, 一定等于a吗?
1. 的化简:2. 的化简:
下列结论正确的是( )A.- =-6 B .(- )2=9C. =±16 D.
1. 定义:若x2=a,则x叫做a的平方根.2. 性质:一个正数有两个平方根,它们互为相反数, 0的平方根是0,负数没有平方根.3. 平方根与开平方间的关系: (1)开平方是求平方根的运算; (2)平方根是开平方运算的结果.
数学八年级上册4.1 平方根完整版课件ppt: 这是一份数学八年级上册4.1 平方根完整版课件ppt,共56页。PPT课件主要包含了1平方根,特别解读,易错警示,知识储备,1练习等内容,欢迎下载使用。
苏科版八年级上册4.1 平方根教学ppt课件: 这是一份苏科版八年级上册4.1 平方根教学ppt课件,共20页。PPT课件主要包含了学习目标,课时讲解,课时流程,课时导入,知识点,感悟新知,课堂小结等内容,欢迎下载使用。
初中数学苏科版八年级上册第四章 实数4.1 平方根教学课件ppt: 这是一份初中数学苏科版八年级上册第四章 实数4.1 平方根教学课件ppt,共25页。PPT课件主要包含了学习目标,课时讲解,课时流程,课时导入,知识点,算术平方根的定义,感悟新知,求算术平方根,算术平方根的非负性,非负数等内容,欢迎下载使用。













