





初中数学苏科版八年级上册第四章 实数4.1 平方根教学课件ppt
展开算术平方根的定义求算术平方根 算术平方根的非负性
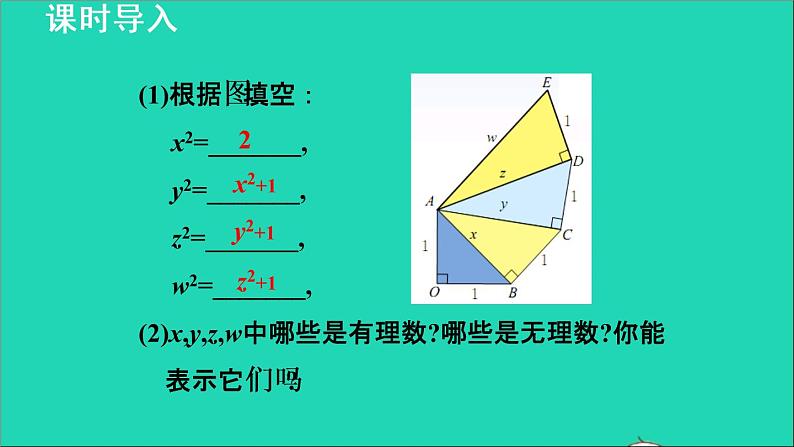
(1)根据图填空: x2=_______, y2=_______, z2=_______, w2=_______,(2)x,y,z,w中哪些是有理数?哪些是无理数?你能 表示它们吗?
问题1:正数3的平方等于9,若x2=9,则正数x=____. 正数4的平方等于16,若x2=16,则正数x=____. 说说6和36这两个数又怎样的关系呢?问题2:(1) 0的平方是___,如果x2=0,那么x=____. (2) 0的算术平方根是___.
问题3:学校要举行美术作品比赛,小鸥想裁出一块 面积为25 dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应 取多少?你一定会算出边长应取5 dm. 说一说,你是怎样算出来的?因为52=25,所以这个正方形画布的边长应取5 dm.
填表:上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
定义:一般地,如果一个正数x的平方等于a, 即x2=a,那么这个正数x就叫做a的算术平方根.规定:0的算术平方根是0.表示方法:正数a的算术平方根表示为 读作 “根号a”.
下列说法正确的是( )A.3是9的算术平方根 B.-2是4的算术平方根C. (-2)2的算术平方根是-2 D.-9的算术平方根是3
要正确把握算术平方根的定义.因为3的平方等于9,所以3是9的算术平方根;因为-2不是正数,所以-2不是4的算术平方根;因为(-2)2 =4,而22=4,所以2是(-2)2的算术平方根;负数没有算术平方根.
算术平方根具有双重非负性:这个数是非负数,它的算术平方根也是非负数.
1 9的算术平方根为( ) A. 3 B.-3 C.±3 D.2 下列说法正确的是( ) A.因为62=36,所以6是36的算术平方根 B.因为(-6)2=36,所以-6是36的算术平方根 C.因为(±6)2=36,所以6和-6都是36的算术 平方根 D.以上说法都不对
(1) 正数的算术平方根是一个正数;(2) 0的算术平方根是0;(3) 负数没有算术平方根;(4) 被开方数越大,对应的算术平方根也越大.
求下列各数的算术平方根:(1) 100; (2) ; (3) 0.0001.
(1)因为102 = 100,所以100的算术平方根是10, 即(2)因为( )2 = ,所以 的算术平方根是 , 即 ;(3)因为0.012 =0.0001,所以0.0001的算术平方 根是0.01,即 =0.01.
(1)求一个数的算术平方根时,首先要弄清是求哪个数 的算术平方根,分清求 与81的算术平方根的不 同意义,不要被表面现象迷惑.(2)求一个非负数的算术平方根常借助于平方运算,因 此熟记常用平方数对求一个数的算术平方根十分有 用.
(1)因为0.052=0.002 5,所以0.002 5的算术平方 根是0.05,即 =0.05;(2)因为92=81,所以81的算术平方根是9, 即 =9;(3)因为32=9,9的算术平方根是3,所以32的算 术平方根是3,即 =3.
求下列各数的算术平方根:(1) 0.0025; (2) 81; (3) 32.
求下列各式的值:(1) ; (2) ; (3) .
问题1: (1)因为_____2=64,所以64的算术平方根是 ______,即 =______.(2)因为_____2=0.25,所以0.25的算术平方根是______, 即 =______.(3)因为_____2=0,所以0的算术平方根是______, 即 =______.
问题2: 讨论:在 中,被开方数a是一个______数, 算术平方根 是一个______数.
所以算术平方根 具有双重非负性:1. 被开方数a是非负数,即a ≥0;2. 算术平方根 本身是非负数,即
若 =0,求x2 015+y2 016的值.
非负数与非负数的和为0当且仅当这两个非负数为0时成立,可列方程求出x,y的值,从而求出代数式的值.∵ ≥0, ≥0, =0,∴x-1=0,y+1=0,∴x=1,y=-1.∴x2 015+y2 016=12 015+(-1)2 016=2.
算术平方根和绝对值一样,都是非负数,当几个非负数的和等于0时,其中每一个非负数都为0.
(1) 中,被开方数a是_______,即a_______0;(2) 是________,即 ________0,即非负数的 算术平方根是_______;负数没有算术平方根, 即当a________0时, 无意义.
下列说法中不正确的有( )①一个数的算术平方根一定是正数;②100的算术平方根是10,记作 =10;③(π-3.14)2的算术平方根是π-3.14;④a2的算术平方根为a.A.1个 B.2个 C.3个 D.4个
1. 表示的是a的算术平方根,由算术平方 根的定义知它具有“双重”非负性:a≥0, ≥0,即算术平方根及它的被开方数都 为非负数.2.对于所有的算术平方根,被开方数越大,对 应的算术平方根也越大;反之亦然.
初中苏科版4.1 平方根教课课件ppt: 这是一份初中苏科版<a href="/sx/tb_c100309_t3/?tag_id=26" target="_blank">4.1 平方根教课课件ppt</a>,共16页。PPT课件主要包含了温故知新,新课讲解,算术平方根的记法,的算术平方根记作,展示点拨,例题详解,发展提高,尝试练习,算术平方根,算术平方根的应用等内容,欢迎下载使用。
初中数学北师大版八年级上册2 平方根优秀ppt课件: 这是一份初中数学北师大版八年级上册2 平方根优秀ppt课件,文件包含第二章实数2平方根课时1算术平方根pptx、第二章实数2平方根课时1算数平方跟doc等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
数学八年级上册4.1 平方根教学ppt课件: 这是一份数学八年级上册4.1 平方根教学ppt课件,共25页。PPT课件主要包含了学习目标,课时讲解,课时流程,课时导入,知识点,平方根的定义,感悟新知,开平方,平方根的性质,求平方根开平方等内容,欢迎下载使用。













