高中数学人教A版 (2019)必修 第一册4.4 对数函数测试题

4.4.3　不同函数增长的差异

基础过关练

题组一　不同函数增长的差异

1.下列函数中,增长速度越来越慢的是 (　　)　　　　　　　　　　　　　　　　　　

A.y=6x B.y=log6x    C.y=x6 D.y=6x

2.某校甲、乙两食堂某年1月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知同年9月份两食堂的营业额又相等,则同年5月份              (　　)

A.甲食堂的营业额较高               B.乙食堂的营业额较高

C.甲、乙两食堂的营业额相同         D.不能确定甲、乙哪个食堂的营业额较高

3.(2020湖南醴陵一中高一上期中)已知函数y1=2x,y2=x2,y3=log2x,在区间(0,+∞)上一定存在x0,当x>x0时(　　)

A.2x>x2>log2x B.x2>2x>log2x     C.log2x>2x>x2 D.log2x>x2>2x

4.某小型贸易公司为了实现年终10万元利润的目标,特制订了一个销售人员年终绩效奖励方案:当销售利润为x万元(4≤x≤10)时,奖金y(万元)随销售利润x(万元)的增加而增加,但奖金总数不超过2万元,同时不超过销售利润的,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg 2≈0.3,lg 3≈0.48,lg 5≈0.7)              (　　)

A.y=0.4x B.y=lg x+1      C.y=  D.y=1.125x

题组二　图象信息迁移问题

5.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图象如图所示,那么水瓶的形状大致是              (　　)

6.(2021山东德州、烟台高一上期中联考)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示他离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,出租车匀速行驶,则下列图象中与上述事件吻合最好的是              (　　)

7.(多选)如图所示的是某受污染的湖泊在自然净化的过程中某种有害物质的剩余量y与净化时间t(月)之间满足的函数关系:y=at(t≥0,a>0,a≠1)的图象.若有害物质的初始量为1,则以下说法中正确的是              (　　)

A.第4个月时,剩余量就会低于

B.每月减少的有害物质的量都相等

C.有害物质每月的衰减率为

D.当剩余量为,, 时,所经过的时间分别是t1,t2,t3,则t1+t2=t3

8.函数f(x)=2x和g(x)=x3的大致图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.

(1)请指出图中曲线C1,C2分别对应的函数;

(2)结合函数图象,判断f(6),g(6),f(2 021),g(2 021)的大小.

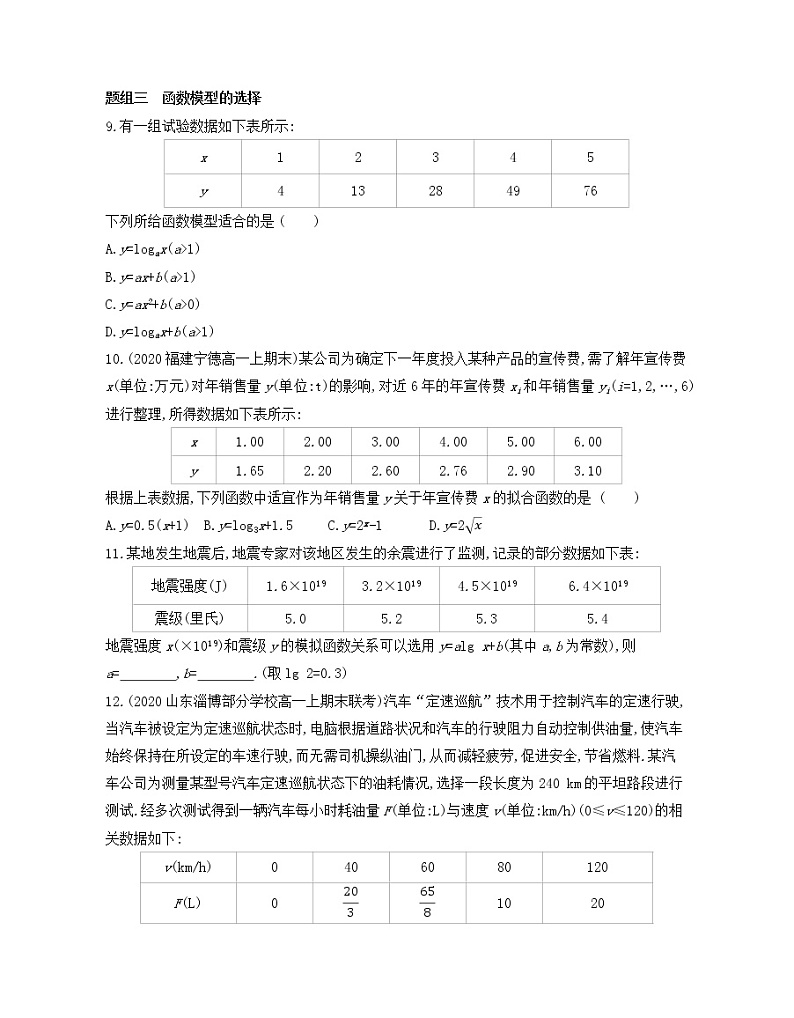
题组三　函数模型的选择

9.有一组试验数据如下表所示:

下列所给函数模型适合的是 (　　)

A.y=logax(a>1)

B.y=ax+b(a>1)

C.y=ax2+b(a>0)

D.y=logax+b(a>1)

10.(2020福建宁德高一上期末)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:t)的影响,对近6年的年宣传费xi和年销售量yi(i=1,2,…,6)进行整理,所得数据如下表所示:

根据上表数据,下列函数中适宜作为年销售量y关于年宣传费x的拟合函数的是 (　　)

A.y=0.5(x+1) B.y=log3x+1.5     C.y=2x-1     D.y=2

11.某地发生地震后,地震专家对该地区发生的余震进行了监测,记录的部分数据如下表:

地震强度x(×1019)和震级y的模拟函数关系可以选用y=alg x+b(其中a,b为常数),则a=　　　　,b=　　　　.(取lg 2=0.3) 

12.(2020山东淄博部分学校高一上期末联考)汽车“定速巡航”技术用于控制汽车的定速行驶,当汽车被设定为定速巡航状态时,电脑根据道路状况和汽车的行驶阻力自动控制供油量,使汽车始终保持在所设定的车速行驶,而无需司机操纵油门,从而减轻疲劳,促进安全,节省燃料.某汽车公司为测量某型号汽车定速巡航状态下的油耗情况,选择一段长度为240 km的平坦路段进行测试.经多次测试得到一辆汽车每小时耗油量F(单位:L)与速度v(单位:km/h)(0≤v≤120)的相关数据如下:

为了描述汽车每小时耗油量与速度的关系,现有以下三种函数模型可供选择:

F(v)=av3+bv2+cv,F(v)=+a,F(v)=klogav+b.

(1)请选出你认为最符合实际的函数模型,并求出相应的函数解析式;

(2)这辆车在该测试路段上以什么速度行驶才能使总耗油量最少?

13.(2020福建厦外高一上期中)某创业投资公司拟投资开发某种新能源产品,估计能获得25万元~1 600万元的投资收益,现准备制订一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.

(1)判断函数f(x)=+10能否作为公司奖励方案的函数模型,并说明理由;

(2)已知函数g(x)=a-5(a≥1)能作为公司奖励方案的函数模型,求实数a的取值范围.

答案全解全析

基础过关练

1.B　D中增长速度不变,A,C中增长速度越来越快,只有B符合题意.

2.A　设甲、乙两食堂该年1月份的营业额均为m,甲食堂的营业额每月增加a(a>0),乙食堂的营业额每月增加的百分率为x,由题意可知,m+8a=m×(1+x)8,则5月份甲食堂的营业额y1=m+4a,乙食堂的营业额y2=m×(1+x)4=.

因为-=(m+4a)2-m(m+8a)=16a2>0,所以y1>y2.

故同年5月份甲食堂的营业额较高.

3.A　由于指数函数增长最快,对数函数增长最慢,因此当x很大时,指数函数值最大,对数函数值最小,

即在区间(0,+∞)上一定存在x0,当x>x0时,2x>x2>log2x,故选A.

4.B　A选项中,当x=10时,y=4,超过2万元,不符;

B选项中,y=lg x+1在[4,10]上是增函数,x=10时,ymax=2,结合图象知,lg x+1<在x∈[4,10]上恒成立,故B符合;

C选项中,当x=10时,y=>2,超过2万元,不符;

D选项中,当x=10时,y=,

设=a,则lg a=10(lg 9-lg 8)=10(2lg 3-3lg 2)≈0.6.

因此a≈100.6>>2,超过2万元,不符.故选B.

5.B　水深h为自变量,随着h的增大,A项中V的增长速度越来越快,C项中先慢后快,D项中增长速度不变,只有B项中V的增长速度越来越慢.

6.C　由题意知,该高三学生从家出发去高铁站,y是x的一次函数,且斜率为正;他返回家取身份证的过程中,y仍然是x的一次函数,斜率为负;他最后从家到高铁站,y仍然是x的一次函数,斜率为正值,且斜率比第一段的斜率大,结合图象可知,与题干中事件吻合最好的图象为C.故选C.

7.ACD　根据图象过点可知,=a2,解得a=或a=-(舍去),

∴函数关系是y=.

令t=4,得y=<,故A正确;

当t=1时,y=,减少了,当t=2时,y=,减少了,每月减少的有害物质的量不相等,故B不正确;

因为y==,所以有害物质每月的衰减率为,故C正确;

分别令y=,,,解得t1=,t2=,t3=,则t1+t2=t3,故D正确.

故选ACD.

8.解析　(1)曲线C1对应的函数为g(x)=x3,曲线C2对应的函数为f(x)=2x.

(2)∵f(1)=2>g(1)=1,f(2)=4<g(2)=8,f(9)=512<g(9)=729,f(10)=1 024>g(10)=1 000,

∴1<x1<2,9<x2<10,

∴x1<6<x2,2 021>x2.

由题图可以看出,当x1<x<x2时,

f(x)<g(x),∴f(6)<g(6).

当x>x2时,f(x)>g(x),

∴f(2 021)>g(2 021).

又g(2 021)>g(6),

∴f(2 021)>g(2 021)>g(6)>f(6).

9.C　通过题中所给数据可知,随着x的增大,y的增长速度越来越快,而A,D中的函数增长速度越来越慢,B中的函数增长速度保持不变,故选C.

10.B　由题表知,当自变量每增加1个单位时,函数值依次增加0.55,0.40,0.16,0.14,0.20,因此A,C不符合题意;当x取1,4时,y=2的值分别为2,4,与题表中的数据相差较大,故选B.

11.答案　;

解析　由题表中数据得

两式相减得a(lg 3.2-lg 1.6)=0.2,

所以alg 2=0.2,解得a=,

所以b=5-lg 1.6=5-(4lg 2-1)=5-×=.

则y=lg x+,

经检验,后两次数据也适合该式.

12.解析　(1)由题意可知,符合本题的函数模型必须满足定义域为[0,120],且在[0,120]上为增函数.

函数F(v)=+a在[0,120]上是减函数,所以不符合题意,

而函数F(v)=klogav+b中的v≠0,即定义域不可能为[0,120],也不符合题意,

所以选择函数F(v)=av3+bv2+cv.

由已知数据得解得

所以F(v)=v3-v2+v(0≤v≤120).

(2)设这辆车在该测试路段的总耗油量为y L,行驶时间为t h,由题意得

y=F·t=·

=v2-v+70=(v-80)2+30,

因为0≤v≤120,所以当v=80时,y有最小值,最小值为30.

所以这辆车在该测试路段上以80 km/h的速度行驶时总耗油量最少,最少为30 L.

13.解析　(1)不能,理由:对于函数模型f(x)=+10,

当x∈[25,1 600]时, f(x)是单调递增函数,则f(x)≤f(1 600)<75,显然恒成立,若函数f(x)≤恒成立,则+10≤,解得x≥60.

∴f(x)≤不一定成立.

故函数模型f(x)=+10不符合要求.

(2)当x∈[25,1 600]时,g(x)=a-5(a≥1)单调递增,

∴最大值g(1 600)=a-5=40a-5≤75,∴a≤2.

设g(x)=a-5≤恒成立,

则a2x≤恒成立,即a2≤+2+.

∵+≥2,当且仅当x=25时取等号,∴a2≤2+2=4.

∵a≥1,∴1≤a≤2.

综上,a的取值范围为[1,2].