

- 4.3对数的概念及运算学案 学案 5 次下载
- 4.3对数第二课时学案 学案 2 次下载
- 4.4对数函数第二课时学案 学案 6 次下载
- 4.4对数函数第三课时学案 学案 6 次下载
- 4.5函数的应用(二)第一课时学案 学案 6 次下载
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数精品第一课时导学案
展开第四章 指数函数与对数函数
4.4对数函数
第1课时对数函数的概念
【课程标准】
- 理解对数函数的概念、图像及性质。
- 会解与对数函数有关的定义域、值域、比较大小等问题
【知识要点归纳】
- 对数函数的概念
一般地,把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,定义域是(0,+∞)
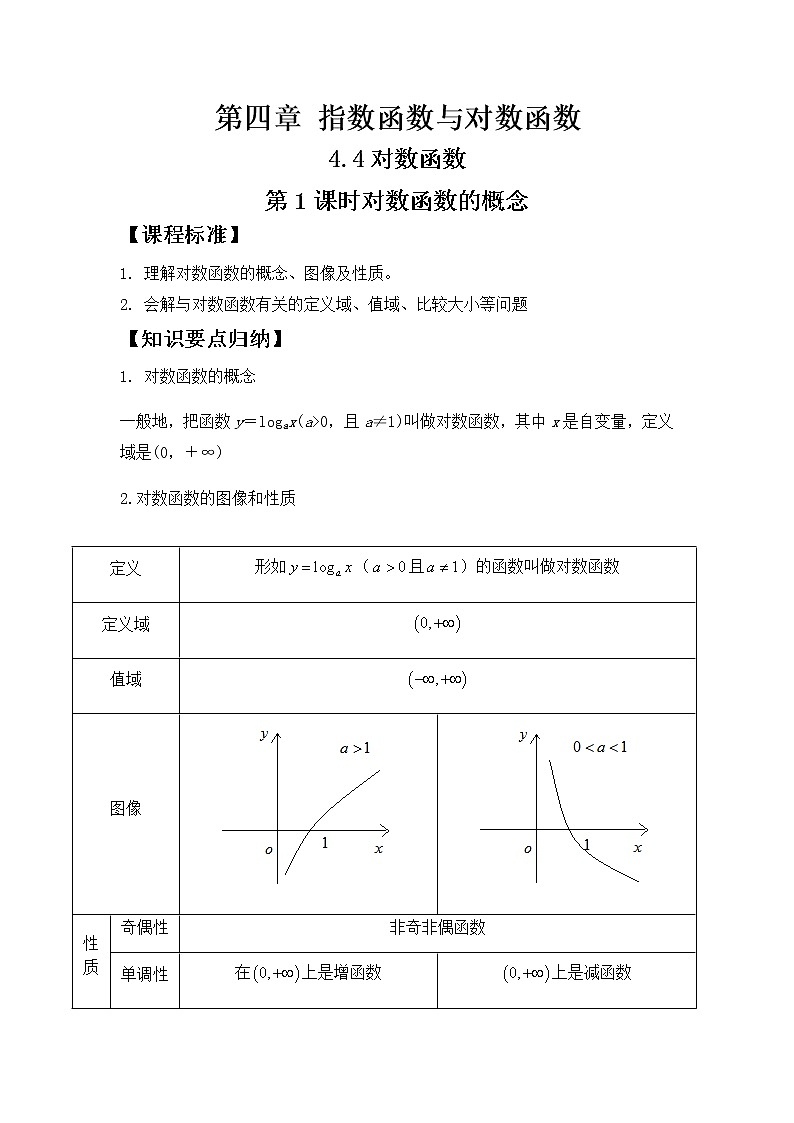
2.对数函数的图像和性质
定义 | 形如(且)的函数叫做对数函数 | ||
定义域 | |||
值域 | |||
图像 | |||
性质 | 奇偶性 | 非奇非偶函数 | |
单调性 | 在上是增函数 | 上是减函数 | |
范围 | 当时,; 当时, | 当时,; 当时, | |
定点 | |||
| 对称性 | ||
【经典例题】
例1 指出下列函数哪些是对数函数?.
[跟踪训练]1(1)对数函数的图象过点M(16,4),则此对数函数的解析式为 。
(2)若对数函数y=f(x)满足f(4)=2,则该对数函数的解析式为( )
A.y=log2x B.y=2log4x
C.y=log2x或y=2log4x D.不确定
注意:判断一个函数是对数函数必须是形如y=logax(a>0且a≠1)的形式,即必须严格满足以下条件:
(1)系数为1.
(2)底数为大于0且不等于1的常数.
(3)对数的真数仅有自变量x.
例2 求下列函数的定义域.
(1)y=loga(3-x)+loga(3+x);
(2)y=log2(16-4x).
[跟踪训练]2 求下列函数的定义域.
(1)y=;(2)y=;
(3)y=;(4)y=log(x+1)(2-x).
注意:求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.
例3 画出函数y=lg|x-1|的图象.
例4 (1)函数y=x+a与y=logax的图象只可能是下图中的( )
(2)函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.
[跟踪训练] 3 (1) 已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
(2)图象恒过定点坐标是________.
注意:(1)明确图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数a的取值范围是a>1,还是0<a<1.
(3)牢记特殊点.对数函数y=logax(a>0,且a≠1)的图象经过点:(1,0),(a,1)和.
【当堂检测】
一.选择题(共5小题)
1.下列函数是对数函数的是
A. B.,且
C. D.
2.函数为对数函数,则等于
A.3 B. C. D.
3.函数的定义域是
A. B. C.,, D.,,
4.函数的定义域是
A. B., C., D.
5.已知,,,则
A. B. C. D.
二.填空题(共3小题)
6.已知,,,将、、由小到大的顺序排列为 .
7.已知且的图象过定点,点在指数函数的图象上,则 .
8.已知函数,实数,满足(a)(b),则的值为 .
三.解答题(共1小题)
9.设函数.
(1)求函数的定义域;
(2)若对任意实数,关于的方程总有解,求实数的取值范围.
当堂检测答案
一.选择题(共5小题)
1.下列函数是对数函数的是
A. B.,且
C. D.
【分析】根据对数函数的定义即可得出.
【解答】解:根据对数函数的定义可得:只有为对数函数.
故选:.
【点评】本题考查了对数函数的定义,考查了推理能力与计算能力,属于基础题.
2.函数为对数函数,则等于
A.3 B. C. D.
【分析】由对数函数定义推导出,由此能求出.
【解答】解:函数为对数函数,
,解得,
,
.
故选:.
【点评】本题考查函数值的求法,是基础题,解题时要认真审题,注意对数性质的合理运用.
3.函数的定义域是
A. B. C.,, D.,,
【分析】令对数的真数大于0;分母非0,列出不等式组,求出函数的定义域.
【解答】解:要使函数有意义,需满足
解得且
故选:.
【点评】求函数的定义域:常需考虑开偶次方根的被开方数大于等于0;对数的真数大于0底数大于0且不等于1;分母不为0等.注意函数的定义域一定以集合形式或区间形式表示.
4.函数的定义域是
A. B., C., D.
【分析】可看出,要使得函数有意义,则需满足,解出的范围即可.
【解答】解:要使有意义,则:;
;
的定义域为.
故选:.
【点评】考查函数定义域的定义及求法,指数函数的单调性.
5.已知,,,则
A. B. C. D.
【分析】利用指数式和对数式的性质,比较三个数与0或1的大小得答案.
【解答】解:,
,
.
故选:.
【点评】本题考查对数值的大小比较,关键是注意利用0和1为媒介,是基础题.
二.填空题(共3小题)
6.已知,,,将、、由小到大的顺序排列为 .
【分析】由,即可得出,,的大小关系.
【解答】解:,,,
.
故答案为:.
【点评】本题考查了对数函数、指数函数的单调性,考查了计算能力,属于基础题.
7.已知且的图象过定点,点在指数函数的图象上,则 .
【分析】求出定点,代入指数函数中,求出,得到.
【解答】解:由的任意性,时,,故且的图象过定点,
把代入指数函数,且,得,
所以,
故答案为:.
【点评】考查对数函数的定点问题,和求指数函数的解析式,基础题.
8.已知函数,实数,满足(a)(b),则的值为 1 .
【分析】由已知条件,不妨令,又是一个增函数,且(a)(b),故可,则,由此可得的值.
【解答】解:(a)(b),
.
不妨设,则由题意可得,
,,
,
,
故答案为:1.
【点评】本题主要考查对数函数的性质、函数的单调性、函数的值域,考查对数函数单调性的应用,属于基础题.
三.解答题(共1小题)
9.设函数.
(1)求函数的定义域;
(2)若对任意实数,关于的方程总有解,求实数的取值范围.
【分析】(1)由真数大于0,可得,对 分类讨论即可求得定义域;
(2)对任意实数,方程总有解,等价于函数的值域为,由△即可求得的取值范围.
【解答】解:(1)由有意义,
可得,
当时,的定义域为;
当时,的定义域为;
当时,的定义域为.
(2)对任意实数,方程总有解,
等价于函数的值域为,
即能取遍所有正数即可,
所以△,,
实数的取值范围,.
【点评】本题主要考查函数的定义域与值域,考查对数函数的性质,属于中档题,
高中4.4 对数函数学案: 这是一份高中4.4 对数函数学案,共10页。
人教A版 (2019)必修 第一册4.4 对数函数导学案及答案: 这是一份人教A版 (2019)必修 第一册4.4 对数函数导学案及答案,共8页。学案主要包含了问题探究,典例解析,达标检测等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.4 对数函数导学案及答案: 这是一份人教A版 (2019)必修 第一册4.4 对数函数导学案及答案,共10页。














