初中数学19.2.2 一次函数优秀课件ppt

这是一份初中数学19.2.2 一次函数优秀课件pptPPT课件主要包含了复习提问，可以有不同取法吗，创设情境提出问题，提出问题形成思路，y-x+3，初步应用感悟新知，整理归纳，从数到形，从形到数，综合运用等内容，欢迎下载使用。

1、正比例函数的解析式为： 当x=0时，y= 当x=1时，y=所以，它的图像必经过点（ ）( )
y= kx,(k≠0)
2、一次函数的解析式为：
y=kx+b(k≠0)
当x=0时，y= 当y=0时，x= 或当x=1时，y= 所以，它的图像必经过点（ ）和点（ ）或（ ）
3、正比例函数的图象是什么？ 如何画出正比例函数的图象？
4、一次函数的图象是什么？ 如何画出一次函数的图象？
（0 ，b）（1 ，k+b）
或 以确定特殊自变量0、1来定两点
以坐标轴上坐标特点来确定两点
2．反思：在作这两个函数图象时，分别描 了那几点？
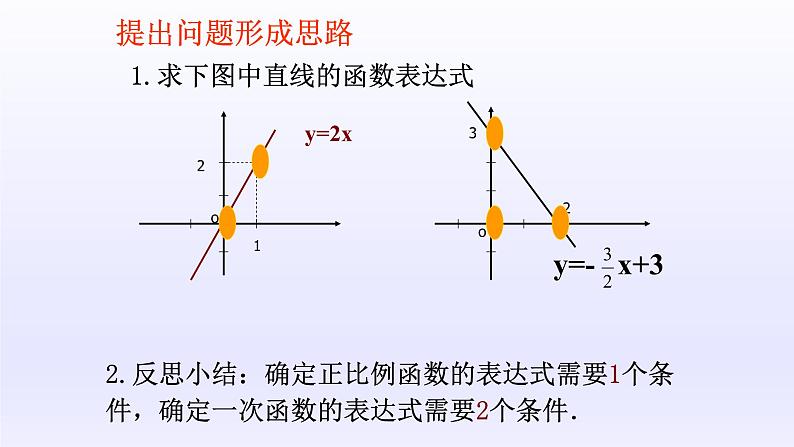
1.求下图中直线的函数表达式
2.反思小结：确定正比例函数的表达式需要1个条件，确定一次函数的表达式需要2个条件．
例题：已知一次函数的图象经过点(3,5)与（－4，－9）.求这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点（3，5）与（-4，-9）.
∴这个一次函数的解析式为y=2x-1
象这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定系数法.
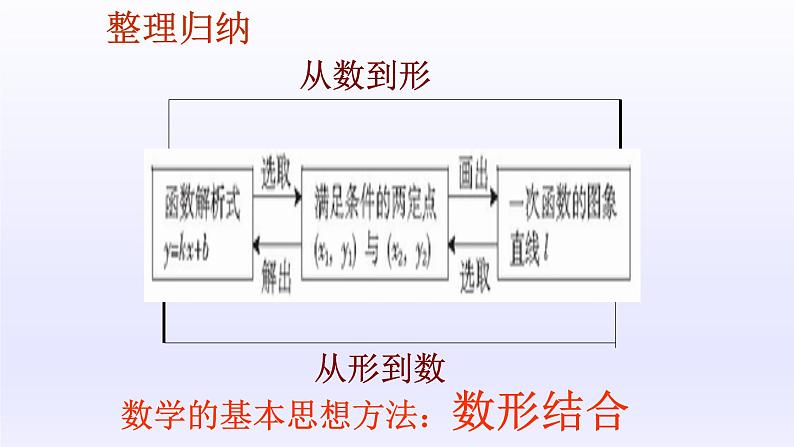
数学的基本思想方法：数形结合
2．若一次函数y=3x-b的图象经过点P(1，－1)，则该函数图象必经过点（ ） A （－1，1） B (2，2) C （－2，2） D (2，一2)
3、若直线y=kx+b平行直线y=-3x+2，且在y轴上的的交点坐标为(0,-5)，则k= ，b= 。
1．已知一次函数y=kx+2，当x=5时y值为4，求k的值.
4. 小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看，该空格里原来填的数是多少？解释你的理由。
2、已知一次函数 的自变量x=3时，函数值y=5；当 x=-4时，y=-9。根据解决上面问题的经验，你能写出这个一次函数的解析式吗？
3、 根据图象，求出相应的函数解析式：
4、 已知直线 y=kx+b 经过点（9，10）和点（24，20），求k与b。
应用待定系数法的一般步骤：（1）写出函数解析式的一般形式，其中包括未知的系数（需要确定这些系数，因此叫做待定系数法）；（2）把自变量与函数的对应值代入函数解析式中，得到关于待定系数的方程或方程组；（3）解方程（方程组）求出待定系数的值，从而写出函数解析式。
1.用待定系数法求函数解析式的一般步骤.
2.数形结合解决问题的一般思路。
一次函数y=kx+b特点是： 自变量x的k（常数）倍与一个常数b的和（即，一次整式）
特别注意应用：k ≠ 0，自变量x的指数是“1”
特别地，当b=0时，一次函数y=kx+b变为y=kx，所以说正比例函数是一种特殊的一次函数
一般地，形如y=kx+b (k、b为常数， k ≠ 0）的函数，y叫做x的一次函数。（x为自变量，y为因变量。）
  例:已知函数y=(m+1)x+(m2-1),当m取什么值时， y是x的一次函数？当m取什么值时，y是x的正比例函数？
解：（1）因为y是x的一次函数所以 m+1 ≠ 0 m≠-1
（2）因为y是x的正比例函数 所以 m2-1=0 m=1或-1
又因为 m≠ -1 所以 m=1
2、函数y=(m – 1)x+1是一次函数，且y随自变量x增大而减小，那么m的取值为__________
3、已知一次函数y=2x+4的图象上有两点A（3，a），B（4，b），则a与b的大小关系为_________
4、一次函数y=(m2+3)x-2,y随x的增大而_________
1.已知一次函数y=（3 – k）x –2k2+18 （1） k为何值时，它的图象经过点（0， – 2）； （2）k为何值时，它的图象经过原点； （3） k为何值时，它的图象与y轴的交点在x轴上方.

2.已知一次函数y=(1－2k)x+k的函数值y随x的增大而增大，且图象经过一、二、三象限，则k的取值范围是__________.
4、若一次函数 y=kx+3的图象经过点(-1,2) ， 则k=_____________
练习2 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值：（1）函数值y 随x的增大而增大；（2）函数图象与y 轴的负半轴相交；（3）函数的图象过第二、三、四象限；（4）函数的图象过原点。
5、某地区电话的月租费为25元，可打50次电话（每次3分钟），超过50次后，每次0.2元，(1)写出每月电话费y（元）与通话次数x（x 50）的函数关系式；(2)求出月通话150次的电话费;(3)如果某月通话费53.6元，求该月的通话次数。