人教版八年级下册19.2.2 一次函数一等奖教学复习课件ppt

这是一份人教版八年级下册19.2.2 一次函数一等奖教学复习课件ppt，文件包含人教版数学八年级下册第十九章《一次函数》章节复习课件pptx、人教版数学八年级下册第十九章《一次函数》章节教学设计docx、人教版数学八年级下册第十九章《一次函数》章节复习导学案docx等3份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

1.回顾总结本章的知识点和知识结构;
2.一次函数的定义、图象和性质的应用; (重点)
3.运用函数思想解决实际问题;(难点)
4.总结本章重要思想方法.
1.变量和常量：变量：在一个变化过程中，数值发生变化的量为变量.常量：在一个变化过程中，数值始终不变的量为常量.
2.函数：一般地，在一个变化过程中，如果有两个变量 x 与 y ，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说 x 是自变量，y 是 x 的函数.
如果当 x = a 时 y = b，那么 b 叫做当自变量的值为 a 时的函数值.
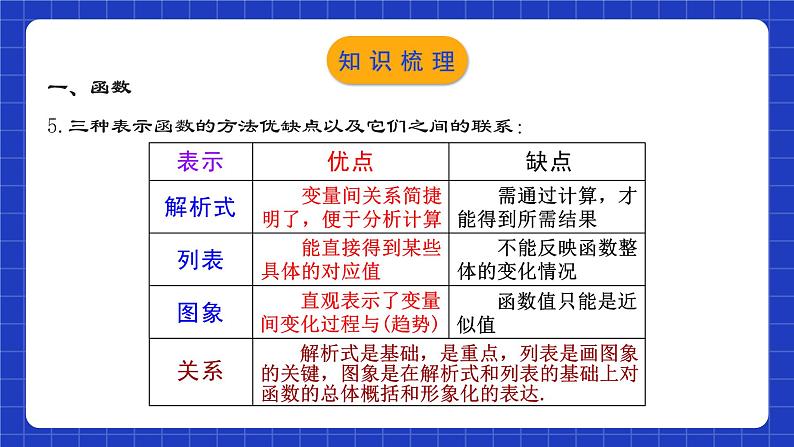
3.函数的图象：对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.如下图的曲线即函数S=x2 (x＞0)的图象.
4.描点法画函数图象的一般步骤：第一步：列表---表中给出一些自变量的值及其对应的函数值；第二步：描点---在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点；第三步：连线---按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来.
5.三种表示函数的方法优缺点以及它们之间的联系：
一般地，形如y=kx(k是常数，k≠0)的函数，叫做正比例函数，其中k叫做比例系数.
一般地，正比例函数y=kx(k是常数，k≠0)的图象是一条经过原点的直线，我们称它为直线y=kx.当k＞0时，直线y=kx经过第三、第一象限，从左向右上升，即随着x的增大y也增大；当k＜0时，直线y=kx经过第二、第四象限，从左向右下降，即随着x的增大y反而减小.
2.正比例函数的图象和性质：
正比例函数y=kx(k≠0)的图象是经过原点和点(1，k)的一条直线.
一般地，形如y=kx+b(k，b是常数，k≠0)的函数，叫做一次函数.特别注意：k≠0，自变量x的指数是1.
当b=0时，y=kx+b就变成了y=kx，所以说正比例函数是一种特殊的一次函数.
4.一次函数的图象的平移规律：
一次函数y=kx+b(k≠0)的图象也是一条直线，我们称它为直线y=kx+b，它可以看作由直线y=kx向上(或向下)平移|b|个单位长度而得到的. 当b＞0时，向上平移；当b＜0时，向下平移.
5.一次函数的图象和性质：
三、用待定系数法求一次函数的解析式
像这样，通过先设定函数解析式（确定函数模型），再根据条件确定解析式中的未知系数，从而求出函数解析式的方法称为待定系数法.
用待定系数法求一次函数解析式的一般步骤：（1）先设出函数解析式；（2）根据条件列关于待定系数的方程（组）；（3）解方程（组）求出解析式中未知的系数；（4）把求出的系数代入设的解析式，从而具体写出这个解析式.
四、一次函数与方程、不等式
1.一次函数与一元一次方程的关系
2.一次函数与一元一次不等式的关系
3.一次函数与二元一次方程组的关系
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组，都对应两个一次函数，于是也对应两条直线.
从“数”的角度看，解这样的方程组，相当于求自变量为何值时相应的两个函数值相等，以及这个函数值是多少；
从“形”的角度看，解这样的方程组，相当于确定两条相应直线交点的坐标. 因此，我们可以用画一次函数图象的方法得到方程组的解.
五、一次函数的实际应用
例2.在全民健身环城越野赛中，甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米. 其中正确的说法有( )A.1个 B.2个 C.3个 D.4个
例3.如图，平面直角坐标系中，在边长为1的正方形ABCD的边上有一动点P沿A→B→C→D→A运动一周，则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
【1-1】根据图中的程序，当输入数值x为-2时，输出数值y为______.
【1-2】小亮从家去学校，为了锻炼身体，一开始跑步前进,跑累了再步行走完余下的路程，下图中，纵轴表示离家的距离，横轴表示出发后的时间，则下列四个图象中较符合该学生走法的是( )
【1-3】小明同学骑自行车去郊外春游，如图表示他离家的距离y(km)与所用的时间x(h)之间关系的函数图象. （1）根据图象回答：小明到达离家最远的地方需______h；（2）小明出发2.5 h后离家_______km；（3）小明出发__________h后离家12 km.
正比例函数的图象与性质
例4.已知正比例函数y＝(2m＋4)x.求：(1)m为何值时，函数图象经过第一、三象限； (2)m为何值时，y随x的增大而减小；(3)m为何值时，点(1，3)在该函数的图象上．
解：∵函数图象经过第一、三象限，∴2m＋4＞0，解得m＞－2.
解：∵y随x的增大而减小，∴2m＋4＜0，解得m＜－2.
例5.若正比例函数y＝(m﹣2)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1＜x2时，y1＞y2，则m的取值范围是（　　）A．m＞0B．m＜0 C．m＞2 D．m＜2
【解析】根据题意，知：y随x的增大而减小，则k＜0，即m﹣2＜0，m＜2．故选：D．
例6.如图，正比例函数y=kx的图象经过点A，点A在第四象限，且横坐标为3.过点A作AH⊥x轴，垂足为点H，且△AOH的面积为3.(1)求正比例函数的解析式;
(2)在x轴上是否存在一点P，使△AOP的面积为5?若存在，求出点P的坐标；若不存在，请说明理由.
例10.如图，正方形A1B1C1O， A2B2C2C1，A3B3C3C2， ...按其所示放置，点A1，A2，A3，…和C1，C2， C3，…分别在直线y=x+1和x轴上，则点B2025的横坐标是___________.
【分析】当x=0时，y=x+1=1，∴A1(0,1)，B1(1，1)易得每一个正方形的边长都是它前一个正方形边长的2倍，因此B2的横坐标为1+1×2=1+2=3=22-1，B3的横坐标为1+1×2+2×2=1+2+4=7=23-1,B4的横坐标为24-1,…，B2025的横坐标为22025-1.
【3-3】已知一次函数y=2x-4.(1)画出它的图象; (2)写出函数图象与x轴、y轴交点的坐标;(3)求这条直线与两坐标轴所围成的三角形面积.
一次函数的“图象共存”问题
两个一次函数y1=ax+b和y2=bx+a (a≠b)在同一直角坐标系中的图象可能是( )
待定系数法求一次函数解析式
例12.若一次函数的图象经过点A(2，0)且与直线y=-x+3平行，求其解析式.
解：设这个一次函数的解析式为y=kx+b.∵一次函数的图象与直线y=-x+3平行∴k=-1把A(2，0)代入y=-x+b中解得b=2∴一次函数的解析式为y=-x+2.
例13.一次函数y=kx+b的自变量的取值范围是-3≤x≤6，相应函数值的取值范围是-5≤y≤-2，求这个函数的解析式.
例14.如图，直线l与y轴交于点(0，3)，与正比例函数y=2x的图象交于点B，且点B的横坐标为1，求直线l对应的函数解析式.
【5-1】一次函数y=mx+|m-1|的图象经过点(0，2)，且y随x的增大而增大，则m的值是_____.【5-2】已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5，则此一次函数的解析式可能为__________________.
y=3x+3或y=-3x+3
【5-3】已知一次函数的图象经过点(9，0)和点(24，20)，写出函数的解析式.
一次函数的平移规律(上、下平移)
【6-3】直线y=6x-5向上平移3个单位，则平移后的直线与y轴的交点坐标是_______.
一次函数与方程、不等式
【7-2】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0；②a>0；③当x<3时，y1【7-4】如图，已知直线y=kx+b经过点B(1，4)，且与直线y=-x-11平行，与直线y=2x- 4交于点C，与x轴交于点A. 求直线AB的解析式及点C的坐标.
(2)已知A类产品个数不超过B类产品的3倍，则制作A、B类两种产品各多少个的时候总收入最多？请说明理由．
例19.为美化深圳市景，园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧，已知搭配一个 A 种造型需甲种花卉 80 盆，乙种花卉 40 盆，搭配一个 B 种造型需甲种花卉 50 盆，乙种花卉 90 盆．(1)问符合题意的搭配方案有几种？请你帮助设计出来；(2)若搭配一个 A 种造型的成本是 800 元，搭配一个 B 种造型的成本是960元，试说明(1)中哪种方案成本最低？最低成本是多少元？
解：设搭配 A 种造型 x 个，则 B 种造型为(50－x)个，依题意，得

∴31≤x≤33.∵x 是整数，x 可取 31,32,33，∴可设计三种搭配方案：①A 种园艺造型 31 个，B 种园艺造型 19 个；②A 种园艺造型 32 个，B 种园艺造型 18 个；③A 种园艺造型 33 个，B 种园艺造型 17 个．
方案①需成本：31×800＋19×960＝43040(元)；
方案②需成本：32×800＋18×960＝42880(元)；
方案③需成本：33×800＋17×960＝42720(元)．
y＝800x＋960(50－x)＝－160x＋48000(31≤x≤33)．
根据一次函数的性质，y 随 x 的增大而减小，
故当 x＝33 时，y 取得最小值为
33×800＋17×960＝42720(元)．
即最低成本是 42720 元．
【8-1】某电器厂生产A、B两种家用小电器，若每天生产A、B两种电器共60件，这两种电器每件的成本和售价如表：设每天生产A种电器x件，每天获得的利润为y元．(1)求y与x之间的函数关系式；(2)如果该电器厂每天最多投入成本为4590元，那么每天生产多少件A种电器时，所获利润最大？并求出这个最大利润．
【8-2】某商场筹集资金12.8万元，一次性购进空调、彩电共30台.根据市场需要，这些空调、彩电可以全部销售，全部销售后利润不少于1.5万元，其中空调、彩电的进价和售价见表格.设商场计划购进空调x台，空调空调彩电和彩电全部销售后商场获得的进价为y元.(1)试写出y与x的函数关系式;(2)商场有哪几种进货方案可供选择?(3)选择哪种方案，商场获利最大?最大利润是多少元?
解: (1) y= (6100-5400)x+ (3900-3500) (30-x)化简，得y=300x+12000
(2)商场有哪几种进货方案可供选择?
(3)选择哪种方案，商场获利最大?最大利润是多少元?
一次函数与几何综合应用
（1）求AB的长和点C的坐标.
（2）求直线CD的解析式．
(1)求S与x之间的函数关系式；