






初中数学人教版八年级下册19.2.2 一次函数获奖课件ppt
展开乌鸦喝水,是《伊索寓言》中一个有趣的寓言故事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶水,于是将小石子投入瓶中,使水面升高,从而喝到了水."告诉人们遇到困难要积极想解决办法,认真思考才能让问题迎刃而解的道理.数学问题也一样哦!
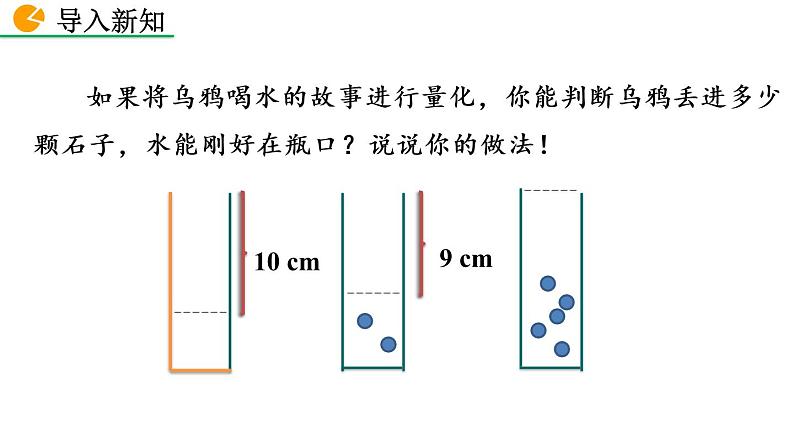
如果将乌鸦喝水的故事进行量化,你能判断乌鸦丢进多少颗石子,水能刚好在瓶口?说说你的做法!
1. 巩固一次函数知识,灵活运用变量关系解决相关实际问题.
3. 有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力.
2. 了解分段函数,会求分段函数的解析式及确定自变量的取值范围.
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
①求出h与d之间的函数解析式(不要求写出自变量d的取值范围). ②某人身高为196 cm,一般情况下他的指距应是多少?
解:(1)设h与d之间的函数关系式为: h=kd+b. 把d=20,h=160,d=21,h=169, 分别代入得, 20k+b=160, 21k+b=169. 解得k=9,b=-20, 即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).
小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:(1)求出y关于x的函数解析式.(2)根据关系式计算,小明经过几个月才能存够200元?
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8,
∴小明经过8个月才能存够200元.
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.(1)填写下表:
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为: .
若购买种子量为0≤x≤2时,种子价格y为: .
y=4(x-2)+10=4x+2
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
叫做分段函数.注意:1.它是一个函数;2.要写明自变量取值范围.
y=5x(0≤x≤2)
y=4x+2(x>2)
一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
当0≤t≤2时,T=20;
当2
T=5t+10(2
1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( ) A.(-1 ,1) B.(2 ,2) C.(-2 ,2) D.(2,-2)2.老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质: 甲:函数的图象经过第一象限; 乙:函数的图象经过第二象限; 丙:在每个象限内,y随x的增大而减小. 请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
y=-2x+6(答案不唯一)
3.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.(2)服药5时,血液中含药量为每毫升____毫克.
(3)当x≤2时y与x之间的函数解析式是___________.(4)当x≥2时y与x之间的函数解析式是___________.(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______小时.
4.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.(1)求y关于x的函数解析式;(2)一箱油可供拖拉机工作几小时?
解:(1)y = -5x + 40.
5.温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
因此摄氏温度与华氏温度的函数关系式为
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过8立方米部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
当x=10时,y=2.7×10-11.2=15.8.
∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害. 某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由.
解:根据图象可知:设0时~5时的一次函数关系式为y1=k1x+b1,经过点(0,3),(5,-3),b1=3, 5k1+b1=-3. 解得k1=-1.2, b1=3.
当y1、y2分别为0时, 而|x2-x1|= >3,∴应采取防霜冻措施.
设5时~8时的一次函数关系式为y2=k2x+b2,经过点(5,-3),(8,5),5k2+b2=-3 , 8k2+b2=5.
∴y1=-1.2x+3.
分段函数的解析式与图象
初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数练习题ppt课件: 这是一份初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数练习题ppt课件,共26页。PPT课件主要包含了学习目标,一次函数解答实际问题,购买种子量,y5x,的函数图象为,解1由题意得,函数解析式为,2函数图像为,链接中考,y3x等内容,欢迎下载使用。
人教版第十九章 一次函数19.2 一次函数19.2.2 一次函数备课ppt课件: 这是一份人教版第十九章 一次函数19.2 一次函数19.2.2 一次函数备课ppt课件,共9页。
人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数教案配套ppt课件: 这是一份人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数教案配套ppt课件,共13页。PPT课件主要包含了复习与激疑,探求新知,s6t,≤t≤2时,<t≤4时,s12,<t≤6时,s-6t+12,巩固练习,9元度等内容,欢迎下载使用。














