高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案

这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案，共24页。
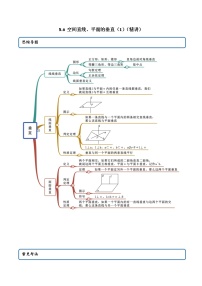
① 直线与直线垂直
(1) 异面直线所成的角
(i) 范围:θ∈(0∘, 90∘]；
(ii) 作异面直线所成的角:平移法.
如图，在空间任取一点O，过O作a' // a, b' // b，则a' , b'所成的θ 角为异面直线a,b所成的角.特别地，找异面直线所成的角时，经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点，端点等)上，形成异面直线所成的角.
(2) 如果两条异面直线所成的角是直角，那么我们就说两条异面直线相互垂直.
② 直线与平面垂直
(1) 定义
若一条直线垂直于平面内的任意一条直线，则这条直线垂直于平面.
符号表述:若任意a⊂α都有l⊥a，则 l⊥α.
(2) 判定定理
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直.
a, b⊂α a∩ b=O l⊥ a l⊥ b⇒l⊥α (线线垂直⇒线面垂直)
(3) 性质
(i) l⊥α, a⊂α⇒ l⊥ a (线面垂直⇒线线垂直)
(ii) 垂直同一平面的两直线平行 a⊥α, b⊥α⇒ a // b
(4) 证明线面垂直的方法
定义法(反证)
判定定理(常用)
a // ba⊥α⇒b⊥α
α // β a⊥α⇒ a⊥β
α⊥β a∩β=b a⊂αa⊥ b⇒ a⊥β(面面垂直⇒线面垂直)
③ 线面所成的角
(1) 定义
如下图，平面的一条斜线(直线l)和它在平面上的射影(AO)所成的角，叫做这条直线和这个平面所成的角.
一条直线垂直平面，则θ=90°；一条直线和平面平行或在平面内，则θ=0°.
(2) 范围
直线和平面所成的角θ的取值范围是0°≤θ≤90°.
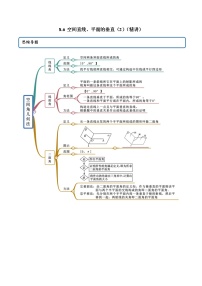
2 面面垂直
① 二面角
(1) 定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
在二面角的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作垂直于棱l的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角.
(2) 范围
二面角的平面角α的取值范围是[0°,180°].
② 面面垂直
(1) 定义
若二面角α−l−β的平面角为90∘，则 α⊥β；
(2) 判定定理
如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.
a⊂ α a⊥β⇒α⊥β (线面垂直⇒面面垂直)
(3) 性质定理
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直.
α⊥βα∩ β=AB a⊂α a⊥ AB⇒ a⊥β (面面垂直⇒线面垂直)
判断
(1) 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥γ ( √ )
(2) 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β ( √ )
(3) 如果平面α⊥平面β，过α内任意一点作交线的垂线，那么此垂线必垂直于β ( × )
(4) 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β ( √ )
【题型一】线面垂直的判定与性质
【典题1】如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点，求证:(1)FD∥平面ABC； (2)AF⊥平面EDB


【典题2】 P为△ABC所在平面外一点，O为P在平面ABC上的射影．
(1)若PA、PB、PC两两互相垂直，则O点是△ABC的 心；
(2)若P到△ABC三边距离相等，且O在△ABC内部，则点O是△ABC的 心；
(3)若PA⊥BC,PB⊥AC,PC⊥AB，则点O是△ABC的 心；
(4)若PA、PB、PC与底面ABC成等角，则点O是△ABC的 心．
【典题3】 如图，在矩形ABCD中，AB=8，BC=4，E为DC边的中点，沿AE将△ADE折起，在折起过程中，有几个正确( )
①ED⊥平面ACD ②CD⊥平面BED ③BD⊥平面ACD ④AD⊥平面BED．
A．1个 B．2个 C．3个 D．4个
【题型二】面面垂直的判定与性质
【典题1】 如图，已知四棱锥P－ABCD中，已知PA⊥底面ABCD，且底面ABCD为矩形，则下列结论中错误的是（ ）
A．平面PAB⊥平面PAD B．平面PAB⊥平面PBC
C．平面PBC⊥平面PCD D．平面PCD⊥平面PAD
【典题2】 如图，直角△ABC中，∠ACB=90°，BC=2AC=4，D、E分别是AB、BC边的中点，沿DE将△BDE折起至△FDE，且∠CEF=60°．
(Ⅰ)求四棱锥F－ADEC的体积；(Ⅱ)求证:平面ADF⊥平面ACF．

【典题3】 长方形ABCD中，AB=2，BC=1，F是线段DC上一动点，且0