高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案

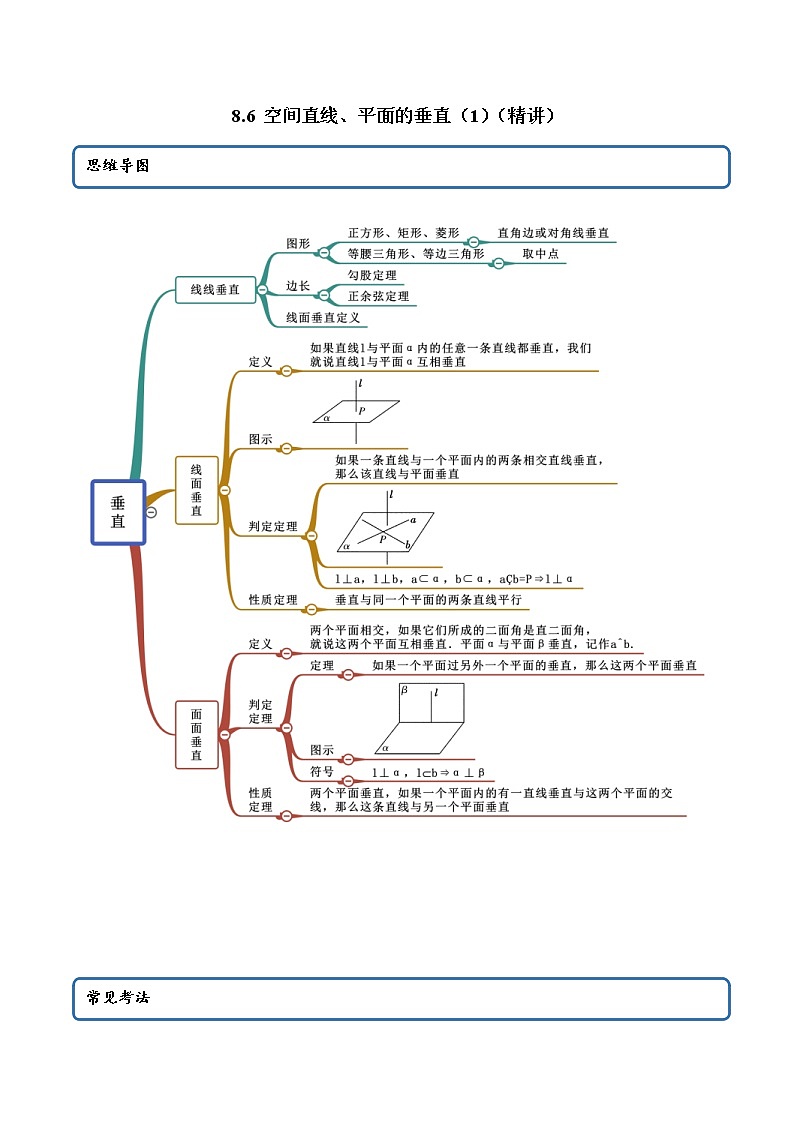
8.6 空间直线、平面的垂直（1）（精讲）

考法一  线面垂直

【例1】（2021·江西景德镇市·景德镇一中）在四棱锥中，，，平面，为的中点，为的中点，．

（1）取中点，证明：平面；

（2）求点到平面的距离.

【答案】（1）证明见解析；（2）

【解析】（1）证明: 因为中点，

在中，，则．

而，则在等腰三角形中，①.

又在中，, 则，

因为平面，平面，则，

又，即，，

则平面，因为平面，所以，因此②.

又，由①②知平面；

（2）在中，，，

又，平面，

平面，即为三棱锥的高，

，

在中，，，

设点到平面的距离为，

则，

，即点到平面的距离为.

【一隅三反】

1．（2021·陕西省黄陵县中学高一期末）如图所示，为的直径，C为上一点，平面，于E，于F.求证：平面.

【答案】证明见解析

【解析】证明：为⊙O的直径，C为⊙O上点，所以

因为平面，平面，所以

又,所以 面

又平面，则

又，，所以平面

又平面，所以

又因为，

所以平面

2．（2021·宁夏银川市·银川一中高一期末）如图，在三棱锥中，平面ABC，底面ABC是直角三角形，，O是棱的中点，G是的重心，D是PA的中点.

（1）求证：平面；

（2）求证：平面；

【答案】（1）证明见解析；（2）证明见解析.

【解析】（1）证明：平面ABC，且平面ABC，，

底面ABC是直角三角形且，，

又平面PAB，平面PAB，，

平面.

(2)证明：连结并延长交于点，连结，,

是的重心， 为边上的中线， 为边上的中点，

又有为边上的中点， ，

平面PBC，平面PBC，

同理可得平面PBC，

又平面DOE，平面DOE，，

平面DOE平面PBC，

又有平面DOE， 平面

3．（2021·陕西咸阳市·高一期末）将棱长为2的正方体沿平面截去一半（如图1所示）得到如图2所示的几何体，点，分别是，的中点.

（Ⅰ）证明：平面；

（Ⅱ）求三棱锥的体积.

【答案】（Ⅰ）证明见解析；（Ⅱ）1.

【解析】（Ⅰ）如图所示：

连接，易知，

因为平面，平面，

所以，又，

所以平面.

在中，点，分别是，的中点，

所以.

所以平面.

（Ⅱ）∵平面，

∴是三棱锥在平面上的高，且.

∵点，分别是，的中点，

∴.

∴.

∴.

考法二  线线垂直

【例2】（2020·全国专题练习）如图，在三棱柱中，侧面为矩形， ，D是的中点，与交于点O，且平面

(1)证明：；

(2)若，求三棱柱的高.

【答案】（1）证明见解析；（2）.

【解析】（1）证明：由题意

且 ,  

,所以,

又侧面， ,又与交于点 ，所以,平面 

又因为 平面,所以．

(2)在矩形中，由平面几何知识可知

∵，∴，

∴

设三棱柱的高为，即三棱锥的高为

又，由得

，∴

【一隅三反】

1．（2021·西安市航天城第一中学高一期末）如图，在三棱柱中，侧棱⊥底面，，分别为棱的中点．

（1）求证：；

（2）若求三棱锥的体积．

【答案】（1）见解析；（2）.

【解析】（1）因为侧棱⊥底面，平面，所以，

因为为中点，，故，而，

故平面，而平面，故.

（2）取的中点为，连接.

因为，故，故，

因为，故，且，故，

因为三棱柱中，侧棱⊥底面，

故三棱柱为直棱柱，故⊥底面，

因为底面，故，而，

故平面，

而，

故.

2．（2021·广西河池市·高一期末）如图，在三棱柱中，，．

（1）若三棱柱的体积为1，求三棱锥的体积；

（2）证明：．

【答案】（1）；（2）证明见解析.

【解析】（1）设三棱柱的高为，的面积为，

由三棱柱的体积为1，可得，

可得三棱锥的体积为.

（2）如图所示：

取的中点，连，,

∵，

∴，

∴,

∵，，

∴

∵，，

∴,

∵，，平面，，

∴平面

∵平面，平面，

∴．

3．（2021·扶风县法门高中高一期末）如图，三棱锥V—ABC中， VA=VB＝AC=BC=，AB＝，VC=1．

（1）证明： AB⊥VC；

（2）求三棱锥V—ABC的体积．

【答案】（1）证明见解析；（2）.

【解析】（1）证明：取AB的中点为D，连接VD，CD，

∵VA=VB，是等腰三角形，∴AB⊥VD，

，是等腰三角形， AB⊥CD，

，所以AB⊥平面VDC．又VC平面VDC，故AB⊥VC.

（2）由（1）知AB⊥平面VDC，

，，所以，

，，又VC=1，所以是等边三角形，

所以，

故三棱锥V—ABC的体积等于．

考法三 面面垂直

【例3】（2021·江西景德镇市·景德镇一中高一期末）如图，四棱锥中，底面是正方形，平面，，为与的交点，为棱上一点.

（1）证明：平面平面；

（2）若平面，求三棱锥的体积.

【答案】（1）证明见解析；（2）.

【解析】（1）因为四边形为正方形，则，

底面，平面，，

，平面，

平面，平面平面；

（2）如下图所示，连接，

四边形为正方形，且，则为的中点，

因为平面，平面，平面平面，，

为的中点，为的中点，

平面，平面，且，

的面积为，

所以，.

【一隅三反】

1．（2021·陕西宝鸡市·高一期末）如图，在三棱锥中，，，，，为线段的中点，为线段上一点．

（1）求证：平面平面；

（2）当面时，求三棱锥的体积．

【答案】（1）证明见解析；（2）．

【解析】（1）证明：由，为线段的中点，    

可得，

由，，，

可得 平面，

又平面，

可得

又  

所以平面，平面，

所以平面平面；

（2）解：平面，平面，

且平面平面，

可得，

又为的中点，

可得为的中点，且，

由平面，可得平面，

可得，

则三棱锥的体积V= ．

2．（2021·全国高一课时练习）在四棱锥中，底面ABCD为矩形，平面PCD，E，F分别为PC，AB的中点求证：

（1）平面平面ABCD；

（2）平面PAD

【答案】（1）证明见解析；（2）证明见解析.

【解析】证明：（1）∵平面PCD，平面PCD

∴

∵ABCD为矩形，∴

又：，平面PAD，平面PAD

∴平面PAD

∵平面ABCD

∴平面平面ABCD

（2）连接AC，BD交于点O，连接OE，OF，

∵ABCD为矩形，∴O点为AC中点

∵E为PC中点

∴

∵平面PAD，平面PAD

∴平面PAD

同理可得：平面PAD

∵

∴平面平面PAD

∵平面OEF

∴平面PAD

3．（2021·全国高一课时练习）如图所示，已知在三棱锥中，，M为的中点，D为的中点，且为正三角形．

（Ⅰ）求证：平面；

（Ⅱ）求证：平面平面；

（Ⅲ）若，求三棱锥的体积．

【答案】（1）见详解；（2）见详解；（3）

【解析】证明：因为为的中点，为的中点，

所以是的中位线，.

又平面，平面，

所以平面.

（2）证明：因为为正三角形，为的中点，所以.

又，所以.

又因为，，所以平面.

因为平面，所以.

又因为，，

所以平面.

(3)因为平面，，

所以平面，即是三棱锥的高.

因为，为的中点，为正三角形，

所以.

由平面，可得，

在直角三角形中，由，可得.

于是.

考法四 空间距离

【例4】（2020·全国专题练习）在棱长为的正方体中求出下列距离：

（1）点到面的距离；

（2）线段到面的距离；

（3）点到面的距离；

（4）到平面的距离.

【答案】（1）；（2）；（3）；（4）.

【解析】（1）因为正方体，则平面，

所以点到面的距离为边长；

（2）因为平面，且平面，

所以线段到面的距离为；

（3）因为平面，

所以点到面的距离为面对角线的AC的，即；

（4）设到平面的距离为h，三棱锥的体积为V，

在中，，则的面积为，

利用等体积法可得：，

所以

【一隅三反】

1．（2020·北京二十中高一期末）如图，正四棱锥的高为，且底面边长也为，则点到平面的距离为（    ）

A． B． C． D．

【答案】A

【解析】由正四棱锥的性质可知，其底面为正方形，

连接、，设交点为点，连接，则平面，且，

底面对角线的长度为，侧棱长度为，斜高，

，

，

设点到平面的距离为，由，即，解得．故选：A.

2．（2020·全国）已知正四棱柱ABCD- A1B1C1D1中 ，AB=2，CC1= E为CC1的中点，则直线AC1与平面BED的距离为

A．2 B． C． D．1

【答案】D

【解析】因为线面平行，所求求线面距可以转化为求点到面的距离，选用等体积法．平面，

到平面的距离等于到平面的距离，由题计算得，在中，，边上的高，所以，所以，利用等体积法，得: ,解得:

3．（2020·全国高一课时练习）已知是长方体，且，，.

（1）写出点A到平面的距离；

（2）写出直线AB到平面的距离；

（3）写出平面与平面之间的距离.

【答案】（1）（2）（3）

【解析】如图.

（1）点A到平面的距离；

（2）∵平面，∴AB到平面的距离；

（3）∵平面平面，∴平面与平面之间的距离.