- 【同步导学案】高中数学人教A版(2019)必修第二册--8.4 空间点、直线、平面之间的位置关系 导学案(原卷版+解析版) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)必修第二册--8.5 空间直线、平面的平行 导学案(原卷版+解析版) 学案 1 次下载
- 【同步导学案】高中数学人教A版(2019)必修第二册--9.1 随机抽样 导学案(原卷版+解析版) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)必修第二册--9.2 用样本估计总体 导学案(原卷版+解析版) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)必修第二册--10.1 随机事件与概率 导学案(原卷版+解析版) 学案 2 次下载
【同步导学案】高中数学人教A版(2019)必修第二册--8.6 空间直线、平面的垂直 导学案(原卷版+解析版)
展开![]() 第八章 立体几何初步
第八章 立体几何初步
8.6 空间直线、平面的垂直
一、异面直线所成的角
1.定义:已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把直线
与 所成的角叫做异面直线a与b所成的角(或夹角).
2.异面直线所成角的范围为 .
二、空间两直线垂直
如果两条异面直线所成的角是 ,那么我们就说这两条异面直线互相垂直.直线a与直线b互相垂直,记作 .
三、直线与平面垂直的定义
定义 | 如果直线l与平面α内的 直线都垂直,我们就说直线l与平面α互相垂直 |
记法 | l⊥α |
有关 概念 | 直线l叫做平面α的 ,平面α叫做直线l的 ,它们唯一的公共点P叫做 |
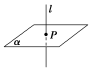
画法 | 画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直 |
图示 |
|
性质 | 过一点垂直于已知平面的直线有且只有一条 |
垂线段与点面距 | 过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离 |
四、直线与平面垂直的判定定理
文字语言 | 如果一条直线与一个平面内的 垂直,那么该直线与此平面垂直 |
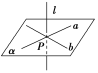
符号语言 | l⊥a,l⊥b,a⊂α,b⊂α, ⇒l⊥α |
图形语言 |
|
五、直线和平面所成的角
斜线 | 一条直线l与一个平面α ,但不与这个平面α ,图中直线PA |
斜足 | 斜线和平面的 ,图中点A |
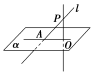
射影 | 过斜线上斜足以外的一点P向平面α引 PO,过 O和 A的直线AO叫做斜线在这个平面上的射影 |
直线和平面所成的角 | 定义:平面的一条斜线和它在平面上的射影所成的角,图中∠PAO 规定:一条直线垂直于平面,它们所成的角是 ;一条直线和平面平行或在平面内,它们所成的角是 |
图示 |
|
取值范围 | [0°,90°] |
六、直线与平面垂直的性质定理
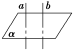
文字语言 | 垂直于同一个平面的两条直线 |
符号语言 | a⊥α,b⊥α⇒ |
图形语言 |
|
作用 | 线面垂直⇒线线平行 |
七、线面距与面面距
1.一条直线与一个平面平行时,这条直线上 到这个平面的距离,叫做这条直线到这个平面的距离.
2.如果两个平面平行,那么其中一个平面内的 到另一个平面的距离都 ,我们把它叫做这两个平行平面间的距离.
八、二面角
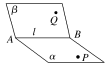
定义 | 从一条直线出发的两个半平面所组成的图形叫作二面角. 这条直线叫作二面角的棱,这两个半平面叫作二面角的面.
如图,记作:二面角α-l-β或二面角P-AB-Q或二面角P-l-Q |
范围 |
|
九、二面角的平面角
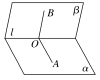
文字语言 | 在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫作二面角的平面角 |
图形语言 |
|
符号语言 | α∩β=l,O∈l,OA⊂α,OB⊂β,OA⊥l,OB⊥l⇒∠AOB为二面角α-l-β的平面角 |
十、平面与平面垂直及判定定理
定义 | 如果两个平面相交,且它们所成的二面角是直二面角,就说这两个平面互相垂直,记作:α⊥β |
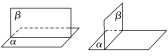
画法 | 通常把直立平面的竖边画成与水平平面的横边垂直,如图: |
判定定理 | 文字表述:一个平面过另一个平面的垂线,则这两个平面垂直. 符号表示: |
十一、平面与平面垂直的性质定理
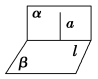
文字语言 | 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直 |
符号语言 |
|
图形语言 |
|
作用 | ①面面垂直⇒线面垂直 ②作面的垂线 |
对面面垂直的性质定理的理解
(1)定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
(2)已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线垂直.
一、单选题
1.设m,n为两条不同的直线,α为平面,则下列结论正确的是( )
A.m⊥n,m∥α⇒n⊥α B.m⊥n,m⊥α⇒n∥α
C.m∥n,m⊥α⇒n⊥α D.m∥n,m∥α=n∥α
2.下列命题中,正确的是( )
A.三点确定一个平面
B.垂直于同一直线的两条直线平行
C.若直线![]() 与平面
与平面![]() 上的无数条直线都垂直,则
上的无数条直线都垂直,则![]()
D.若a、b、c是三条直线,![]() 且与c都相交,则直线a、b、c在同一平面上
且与c都相交,则直线a、b、c在同一平面上
3.如图,上海海关大楼的上面可以看作一个正四棱柱,四个侧面有四个时钟,则相邻两个时钟的时针从0时转到12时(含0时不含12时)的过程中,能够相互垂直( )次

A.0 B.2 C.4 D.12
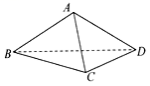
4.已知三棱锥A-BCD中,AD⊥BC,AD⊥CD,则有( )
A.平面ABC⊥平面ADC B.平面ADC⊥平面BCD
C.平面ABC⊥平面BDC D.平面ABC⊥平面ADB
5.ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC,平面PAB与平面PAD的位置关系是( )
A.平面PAB与平面PAD,PBC垂直
B.它们都分别相交且互相垂直
C.平面PAB与平面PAD垂直,与平面PBC相交但不垂直
D.平面PAB与平面PBC垂直,与平面PAD相交但不垂直
6.如图,在三棱锥 ![]() 中,侧面
中,侧面 ![]() 底面BCD,
底面BCD, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,直线AC与底面BCD所成角的大小为
,直线AC与底面BCD所成角的大小为 ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
7.已知 ![]() 是平面
是平面 ![]() 外的一条直线.给出下列三个论断:
外的一条直线.给出下列三个论断:
①![]() ;②
;②![]() ;③
;③![]() .
.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: .
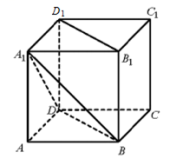
8.如图,已知正方体ABCD–A1B1C1D1的棱长为1,则四棱锥A1–BB1D1D的体积为 .
三、解答题
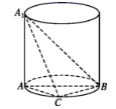
9.如图所示,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,A1A=AB=2.求证:BC⊥平面A1AC.
10.如图,四棱锥 ![]() 满足
满足 ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() .
.
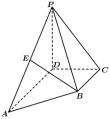
(1)设点 ![]() 为
为 ![]() 的中点,证明:
的中点,证明: ![]() 平面
平面 ![]() ;
;
(2)设平面 ![]() 与平面
与平面 ![]() 的交线为
的交线为 ![]() ,证明:
,证明: ![]() 平面
平面 ![]() .
.
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案: 这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案,共55页。
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案: 这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案,共4页。
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案,共13页。