初中数学北师大版八年级上册第四章 一次函数3 一次函数的图象示范课ppt课件

这是一份初中数学北师大版八年级上册第四章 一次函数3 一次函数的图象示范课ppt课件，共17页。PPT课件主要包含了一次函数与正比例函数，知识回顾，学习目标，课堂导入，新知探究，y2x，y-15x，y-4x，随堂练习等内容，欢迎下载使用。

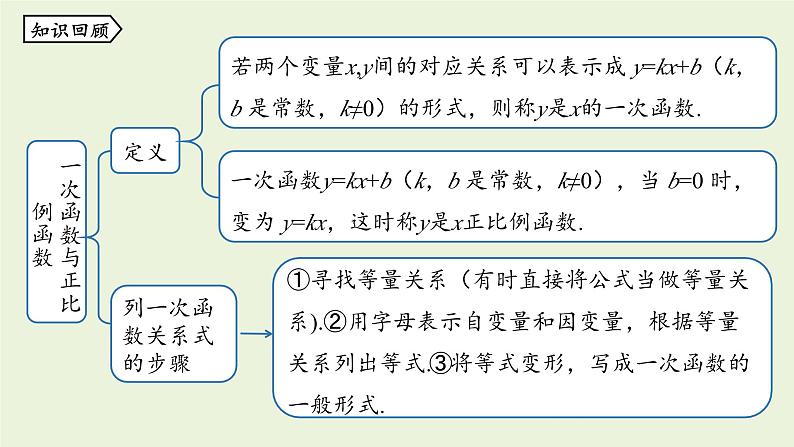
列一次函数关系式的步骤
若两个变量x,y间的对应关系可以表示成 y=kx+b（k，b 是常数，k≠0）的形式，则称y是x的一次函数.
①寻找等量关系（有时直接将公式当做等量关系).②用字母表示自变量和因变量，根据等量关系列出等式.③将等式变形，写成一次函数的一般形式.
一次函数y=kx+b（k，b 是常数，k≠0），当 b=0 时，变为 y=kx，这时称y是x正比例函数.
理解函数图象的概念，初步了解画函数图象的一般步骤。
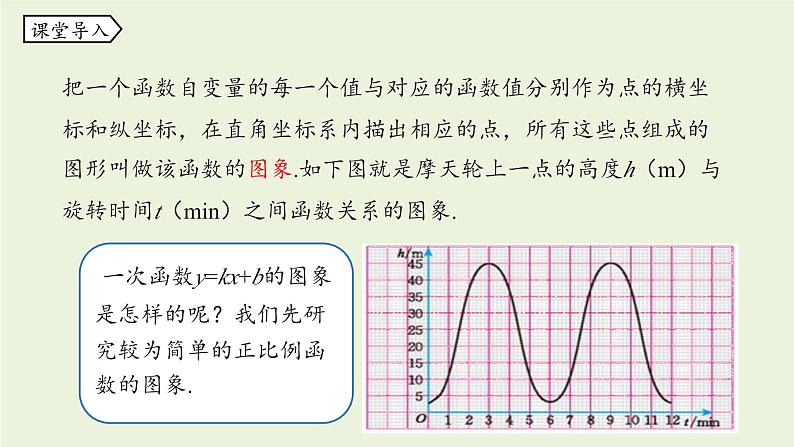
把一个函数自变量的每一个值与对应的函数值分别作为点的横坐标和纵坐标，在直角坐标系内描出相应的点，所有这些点组成的图形叫做该函数的图象.如下图就是摩天轮上一点的高度h（m）与旋转时间t（min）之间函数关系的图象.
一次函数y=kx+b的图象是怎样的呢？我们先研究较为简单的正比例函数的图象.
例 画出下列正比例函数的图象.
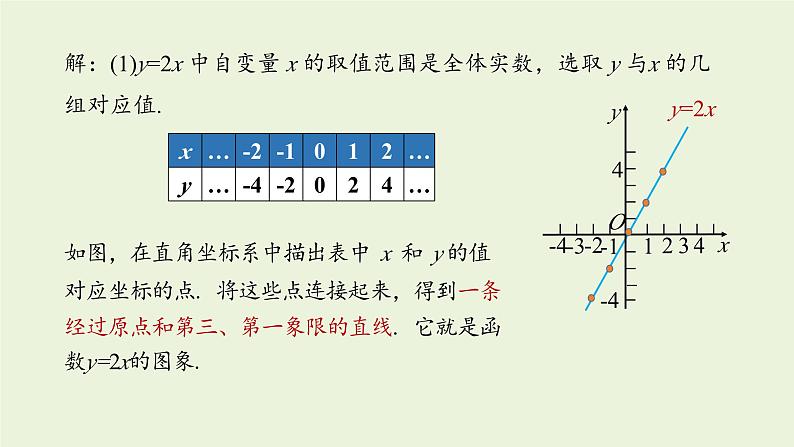
如图，在直角坐标系中描出表中 x 和 y 的值对应坐标的点. 将这些点连接起来，得到一条经过原点和第三、第一象限的直线. 它就是函数y=2x的图象.
解：(1)y=2x 中自变量 x 的取值范围是全体实数，选取 y 与x 的几组对应值.
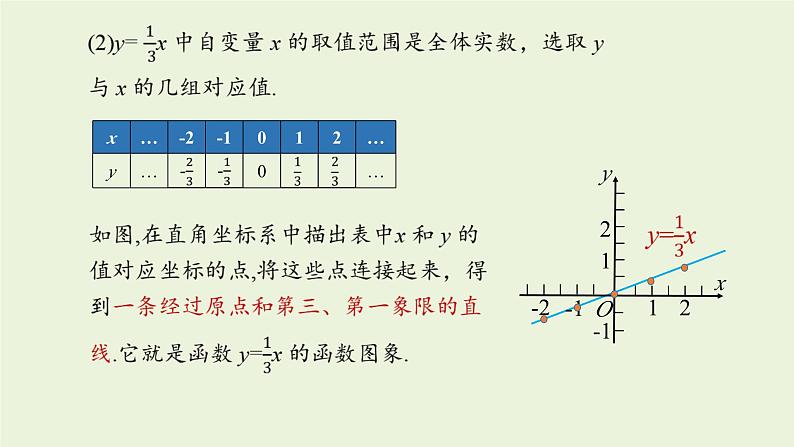
如图，在直角坐标系中描出表中 x 和 y 的值对应坐标的点，将这些点连接起来，得到一条经过原点和第二、第四象限的直线，它就是函数 y=-1.5x 的函数图象.
如图，在直角坐标系中描出表中x 和 y 的值对应坐标的点，将这些点连接起来，得到一条经过原点和第二、第四象限的直线，它就是函数 y=-4x 的函数图象.
知识点一 画函数图象的一般步骤：
列表给出一些自变量的值及其对应的函数值
按照横坐标由小到大的顺序把这些点顺次连接起来
以表中各组对应值作为点的坐标，在直角坐标系中描出相应的各点
知识点二 正比例函数的图象:正比例函数 y=kx（k≠0）的图象是一条经过原点（0,0）的直线，我们称它为直线 y=kx.
知识点三 正比例函数图象的画法：画正比例函数的图象时，通常取（0,0),(1,k)两点，再过这两点画直线，简记为“量点法”作图。
知识点四 正比例函数图象的性质：当k>0时，直线 y=kx 经过第三、第一象限，从左向右上升，即随着 x 的增大 y 也增大；当k<0时，直线 y=kx 经过第二、第四象限，从左向右下降，即随着 x 的增大 y 反而减小.
注意：正比例函数图象的位置和函数的增减性只与 k 的正负有关.
2.函数 y=-5x 的图象经过（ ）.
A. 第一、第二象限 B. 第一、第三象限
C. 第二、第四象限 D. 第三、第四象限
（1）函数y=3x的图象经过第 、 象限，经过点（0， ）和点（ ，3），y随x的增大而 .
（2）函数y=-2x的图象经过第 、 象限，经过点（0， ）和点（-1， ），y随x的增大而 .
3.正确填写下列各空.