人教版八年级数学上册第十二章全等三角形专题二本章重难点教学课件

这是一份人教版八年级数学上册第十二章全等三角形专题二本章重难点教学课件，共32页。

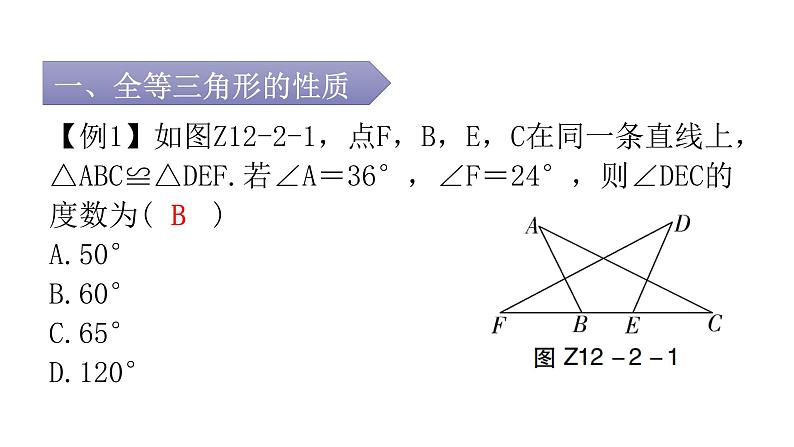
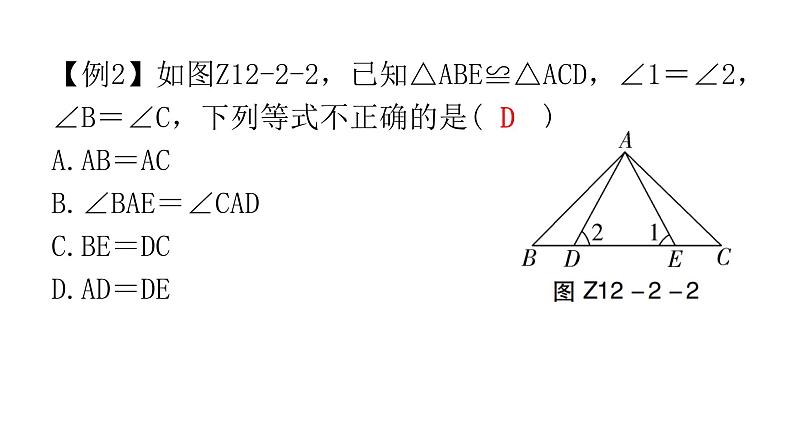
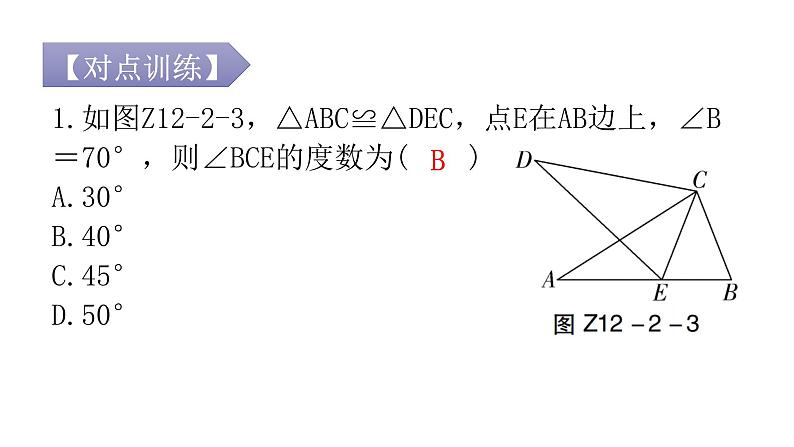
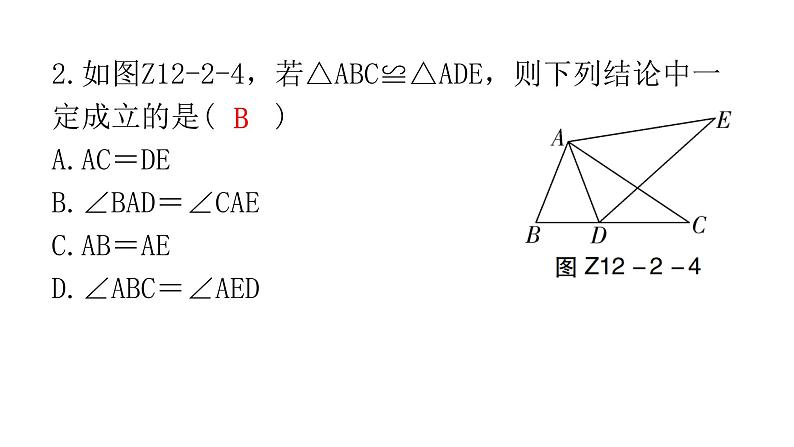
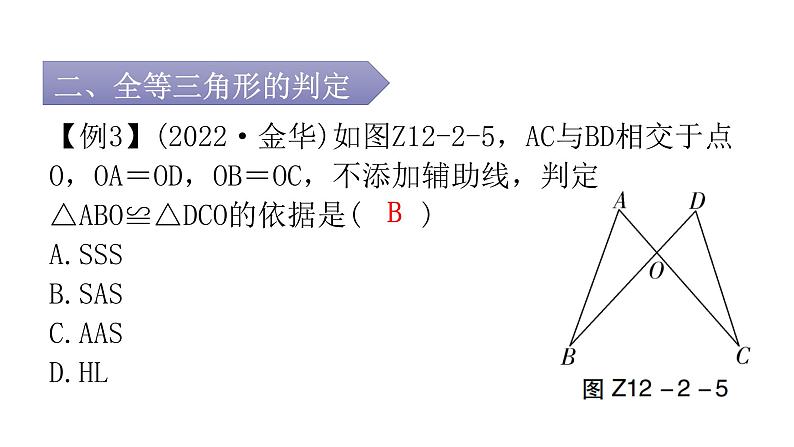
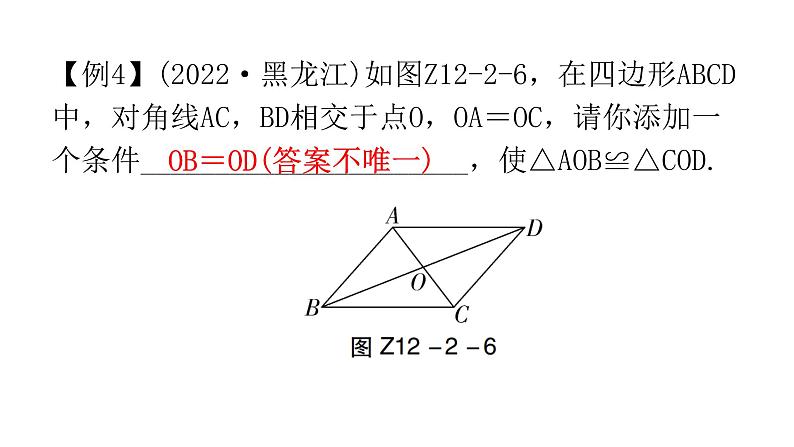
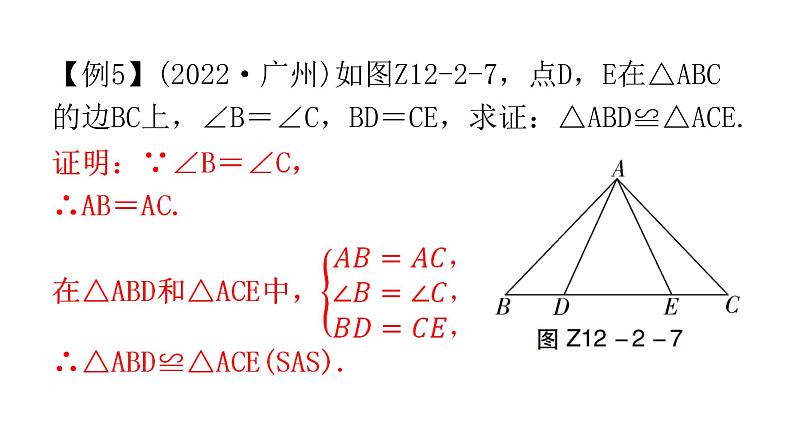
第十二章 全等三角形专题二 本章重难点【例1】如图Z12-2-1，点F，B，E，C在同一条直线上，△ABC≌△DEF.若∠A＝36°，∠F＝24°，则∠DEC的度数为( )A.50° B.60° C.65° D.120°B【例2】如图Z12-2-2，已知△ABE≌△ACD，∠1＝∠2，∠B＝∠C，下列等式不正确的是( )A.AB＝AC B.∠BAE＝∠CAD C.BE＝DC D.AD＝DED1.如图Z12-2-3，△ABC≌△DEC，点E在AB边上，∠B＝70°，则∠BCE的度数为( )A.30° B.40° C.45° D.50°B2.如图Z12-2-4，若△ABC≌△ADE，则下列结论中一定成立的是( )A.AC＝DE B.∠BAD＝∠CAE C.AB＝AE D.∠ABC＝∠AEDB【例3】(2022·金华)如图Z12-2-5，AC与BD相交于点O，OA＝OD，OB＝OC，不添加辅助线，判定△ABO≌△DCO的依据是( )A.SSS B.SAS C.AAS D.HLB【例4】(2022·黑龙江)如图Z12-2-6，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件______________________，使△AOB≌△COD.OB＝OD(答案不唯一)【例5】(2022·广州)如图Z12-2-7，点D，E在△ABC的边BC上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE.【例6】(2022·黄石)如图Z12-2-11，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，且点D在线段BC上，连接CE.(1)求证：△ABD≌△ACE；(2)若∠EAC＝60°，求∠CED的度数.(2)解：∵△ABD≌△ACE，∴∠ACE＝∠ABD.∵△ABC和△ADE都是等腰直角三角形，∴∠ACE＝∠ABD＝∠AED＝45°.∵∠EAC＝60°，∴∠AEC＝180°-∠ACE-∠EAC＝180°-45°-60°＝75°.∴∠CED＝∠AEC-∠AED＝75°-45°＝30°.【例7】在△ABC中，AB=AC，∠BAC=90°，分别过B，C向过点A的直线作垂线，垂足分别为E，F.(1)如图Z12-2-12①，过点A的直线与线段BC不相交时，求证：EF=BE+CF；(2)如图Z12-2-12②，过点A的直线与线段BC相交时，其他条件不变，若BE=10，CF=3，求EF的长.3.如图Z12-2-8，已知∠1=∠2，∠3=∠4，要证BC=CD，证明中判定两个三角形全等的依据是( )A.SSS B.AAA C.ASA D.SASC4.(2022·南通)如图Z12-2-9，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，要使△ABC≌△DEF，只需添加一个条件，则这个条件可以是____________________.AB＝DE(答案不唯一)5.(2022·广东)如图Z12-2-10，已知∠AOC＝∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E.求证：△OPD≌△OPE.6.如图Z12-2-13，已知BE⊥AC于点E，CF⊥AB于点F，BE，CF相交于点D，BF=CE.求证：AE=AF.a-b【例8】如图Z12-2-15，小明站在堤岸的点A处，正对着他的点S处停有一艘游艇．他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离，到达点C处．然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于点D处．通过测量C，D之间的距离，即可得到小明在点A处与游艇的距离．这种方法的原理是( )A.SAS或SSS B.AAS或SSSC.ASA或AAS D.ASA或SASC【例9】在校内劳动课上，小明所在小组的同学们设计了如图Z12-2-16所示的风筝框架.已知∠B＝∠E，AB＝DE，BF＝EC，△ABC的周长为24 cm，FC＝3 cm.制作该风筝框架需用材料的总长度至少为( )A.44 cm B.45 cm C.46 cm D.48 cmB8.(2022·扬州)如图Z12-2-17，小明家仿古家具的一块三角形状的玻璃坏了，需要重新配一块.小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为△ABC，提供下列各组元素的数据，配出来的玻璃不一定符合要求的是( )A.AB，BC，CA B.AB，BC，∠B C.AB，AC，∠B D.∠A，∠B，BCC9.如图Z12-2-18，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD=1 km，DC=1 km，村庄A和C，A和D间也有公路相连，且公路AD是南北走向，AC=3 km，只有A和B之间由于间隔了一个小湖，无直接相连的公路．现决定在湖面上造一座桥，测得AE=1.2 km，BF=0.7 km，则建造的桥长至少为( )A.1.2 km B.1.1 km C.1 km D.0.7 kmB【例10】(2022·北京)如图Z12-2-19，在△ABC中，AD平分∠BAC，DE⊥AB.若AC＝2，DE＝1，则S△ACD＝______.1【例11】如图Z12-2-21，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F.(1)若BE＝CF，求证：AD是∠BAC的平分线；(2)若AD是∠BAC的平分线，求证：BE＝CF.10.如图Z12-2-20，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F.若S△ABC＝21，DE＝3，AB＝9，则AC长是_______.511.(1)如图Z12-2-22①，在四边形ABCD中，BC＞AB，AD＝DC，BD平分∠ABC.求证：∠BAD+∠BCD＝180°；(2)如图Z12-2-22②，D，E，F分别是△ABC的三边上的点，CE＝BF，△DCE和△DBF的面积相等，求证：AD平分∠BAC.