人教版八年级数学上册第十二章全等三角形专题三本章创新考点教学课件

这是一份人教版八年级数学上册第十二章全等三角形专题三本章创新考点教学课件，共22页。

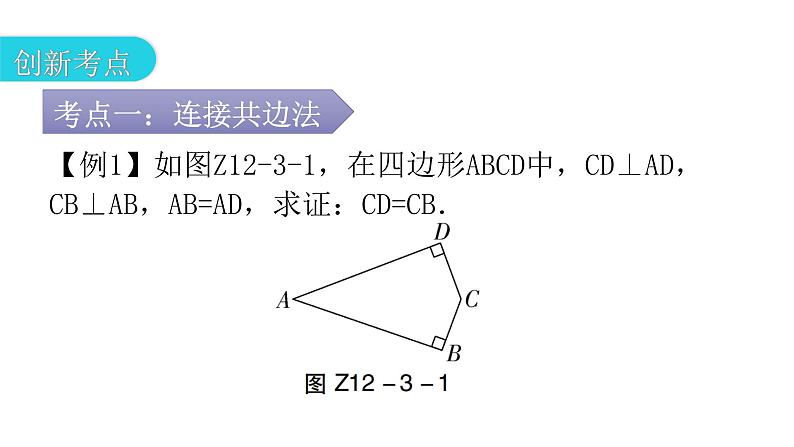
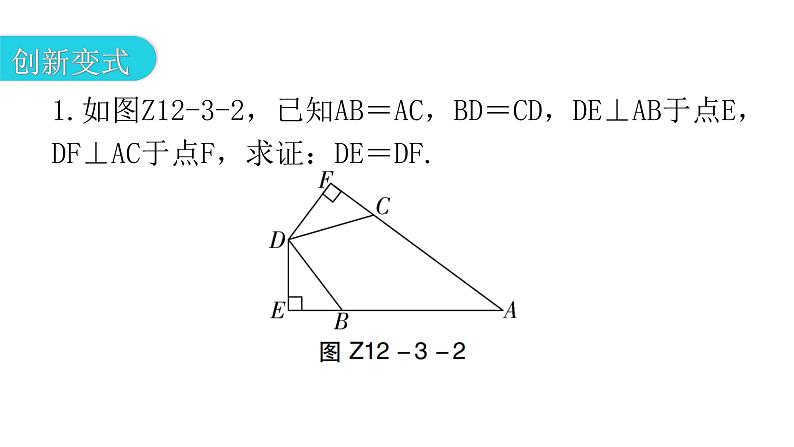
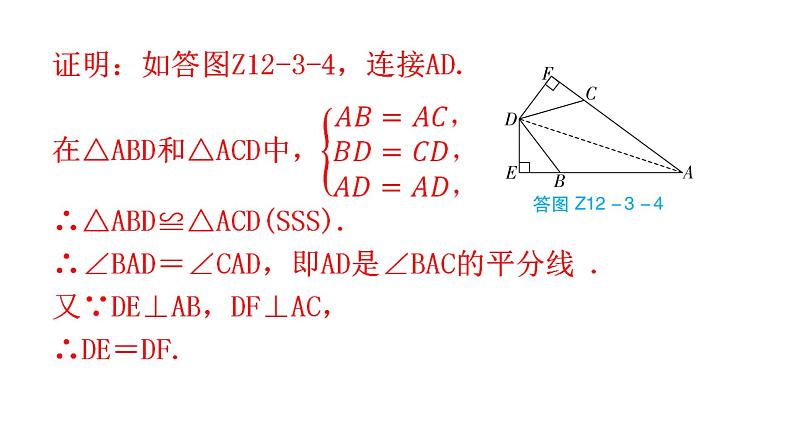
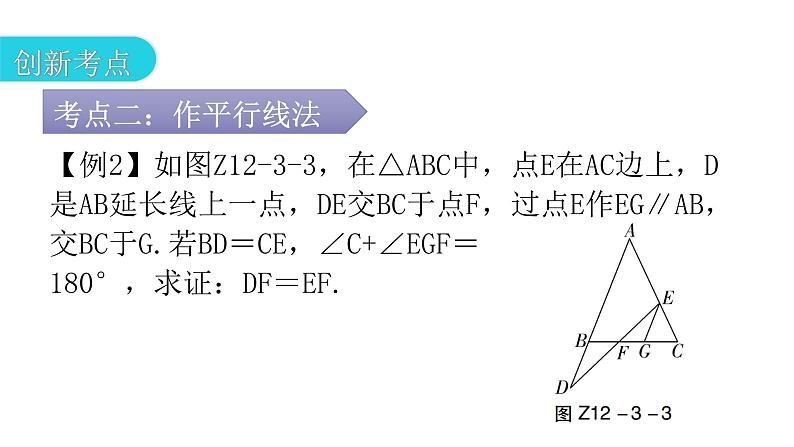
第十二章 全等三角形专题三 本章创新考点01创新考点02创新变式【例1】如图Z12-3-1，在四边形ABCD中，CD⊥AD，CB⊥AB，AB=AD，求证：CD=CB．1.如图Z12-3-2，已知AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE＝DF.【例2】如图Z12-3-3，在△ABC中，点E在AC边上，D是AB延长线上一点，DE交BC于点F，过点E作EG∥AB，交BC于G.若BD＝CE，∠C+∠EGF＝180°，求证：DF＝EF.2.如图Z12-3-4，在△ABC中，D是BC边的中点，过点D的直线交AB于点E，交AC的延长线于点F，且BE＝CF.求证：AE＝AF. 方法归纳：所谓倍长中线法，就是延长三角形的中线，使得延长后的线段是原中线的2倍，目的是为构造一对“8字型”全等三角形(SAS)，从而实现边角的转移.【例3】如图Z12-3-5，已知AB＝4，AC＝2，D是BC的中点，AD是整数，求AD的长.3.如图Z12-3-6，在△ABC中，BD=DC=AC，E是DC的中点，求证：AB=2AE．【例4】如图Z12-3-7，AB∥CD，CE，BE分别平分∠BCD和∠CBA，点E在AD上，求证：BC＝AB+CD.4.如图Z12-3-8，AC平分∠BAD，CE⊥AB于点E，∠B+∠D＝180°.求证：AE＝AD+BE.