
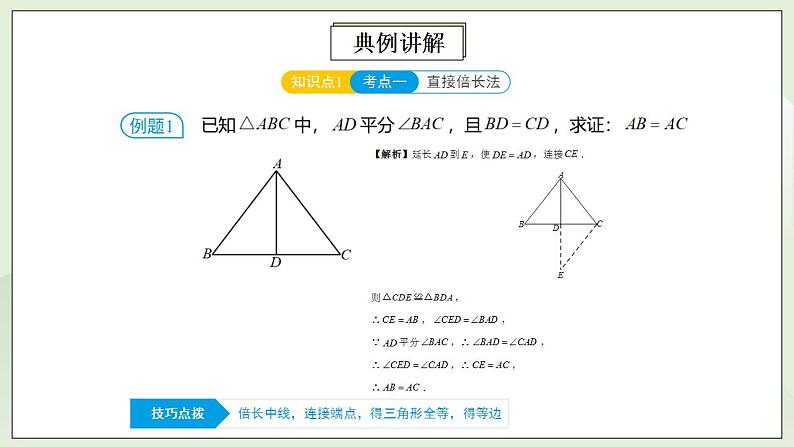

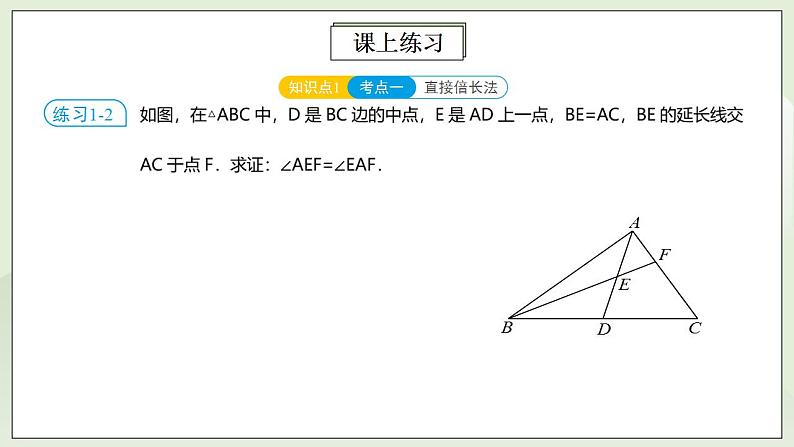








人教版初中数学八年级上册12.5.2第4讲《全等三角形的性质与判定》满分秘诀(二) 课件PPT+教案+分层练习+预习案
展开12.5.2第4讲《全等三角形的性质与判定》满分秘诀(二) 预习案
测试题1 △ABC中,AC=5,中线AD=7,则AB的取值范围为( )
A. 1<AB<29 B. 9<AB<19
C. 5<AB<19 D. 4<AB<14
答案:B
解析过程:延长AD到E,使DE=AD,连接BE,
在△BDE和△CDA中,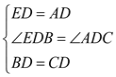 ,
,
则△BDE≌△CDA(SAS),
∴BE=AC=5,DE=AD=7.
在△ABE中,BE=5,AE=14.
利用三角形三边关系可求线段AB的取值范围为:
(14-5)<AB<(14+5),即9<AB<19.所以选B.
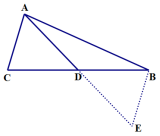
测试题2 如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )

A. BD=DF B. DE=DC
C. BE=CF D. AE=AC
答案:B
解析过程:∵∠1=∠2,∠ACB=∠AED=90°,AD=AD
∴△ADE≌△ACD
∴DE=DC
选B
测试题3 如图所示,已知BE⊥AD交AD的延长线于点E,CF⊥AD于点F,且BE=CF,则下列说法正确的是( )
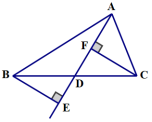
A. AD是△ABC的角平分线
B. AD是△ABC的中线
C. AD既是△ABC的角平分线又是中线
D. 无法确定
答案:B
解析过程:在Rt△BDE和Rt△CDF中
![]() ∠BDE=∠CDF,
∠BDE=∠CDF,
![]() Rt△BDE≌Rt△CDF,∴BD=CD。
Rt△BDE≌Rt△CDF,∴BD=CD。
故AD是△ABC的中线.故选B.
测试题4 如图,D是△ABC的边BC上的点,且CD=AB,∠ADB=∠BAD,AE是△ABD的中线.则AC与AE的数量关系正确的是( )
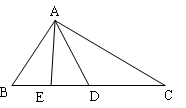
A. AC=2AE B. AC=3AE
C. 2AC=3AE D. 3AC=4AE
答案:A
解析过程:延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,
,
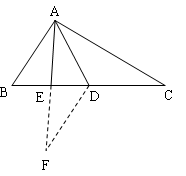
在![]() 与
与![]() 中,
中, ,
,
![]()
![]() (SAS),
(SAS),![]()
![]() ,
,
![]()
![]() ,
,![]()
又![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
在![]() 与
与![]() 中,
中,![]()
 ,
,
![]()
![]() (SAS),
(SAS),![]()
![]() ,
,
又![]()
![]() ,
,![]()
![]() ,所以A正确.
,所以A正确.
测试题5 如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,试说明AD、BC、AB三条线段之间的关系( ).
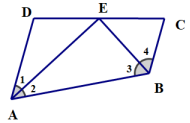
A. AD+BC=AB B. AD-BC=AB
C. AB+AD=BC D. 无法确定
答案:A
解析过程:在AB上取一点F,使AF=AD.连EF.
∵∠1=∠2,AE=AE,∴△ADE≌AFE(SAS),
∴∠D=∠AFE.∵AD∥BC,
∴∠D+∠C=180°.又∵∠AFE+∠BFE=180°,
∴∠C=∠BFE.又∵∠3=∠4,BE=BE,
∴△BEC≌△BEF(AAS),∴BC=BF,
∴AD+BC=AF+BF=AB.
故选:A.
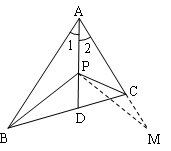
备选题:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上任意一点.则AB-AC与BP-CP的大小关系正确的是( )
上任意一点.则AB-AC与BP-CP的大小关系正确的是( )
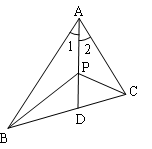
A. AB-AC=BP-CP
B. AB-AC<BP-CP
C. AB-AC>BP-CP
D. 不能确定
答案:C
解析过程:法一:在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
![]()
![]() (SAS),
(SAS),
![]()
![]() ,∴
,∴![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
所以AB-AC>PB-PC.

法二:延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]()
在![]() 与
与![]() 中,
中, ,
,
![]()
![]() (SAS)
(SAS)
![]()
![]() ,∴BP-CP=PM-CP,
,∴BP-CP=PM-CP,
![]() 在
在![]() 中,
中,![]() ,
,
![]()
![]() .所以C正确.
.所以C正确.