人教版八年级上册12.1 全等三角形教学课件ppt

这是一份人教版八年级上册12.1 全等三角形教学课件ppt，共26页。PPT课件主要包含了全等形，全等图形的特征，大小不相同，形状不相同，及时反馈，全等三角形，1平移型，翻折型，旋转型，复合型等内容，欢迎下载使用。

同一张底片洗出的照片是能够完全重合的
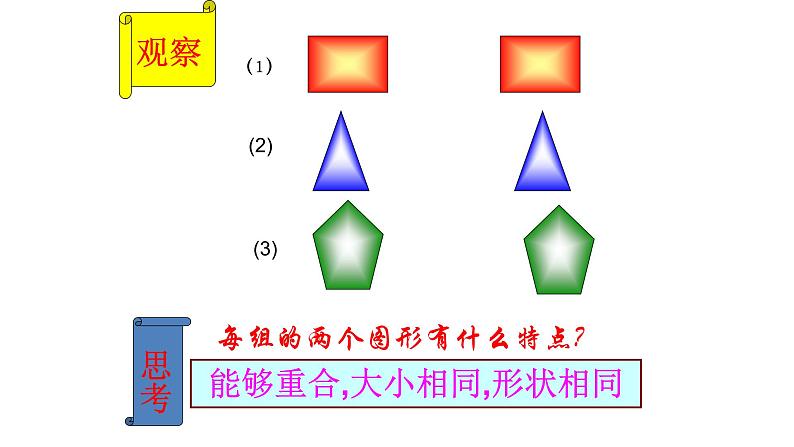
每组的两个图形有什么特点?
能够重合,大小相同,形状相同
能够完全重合的两个图形叫做
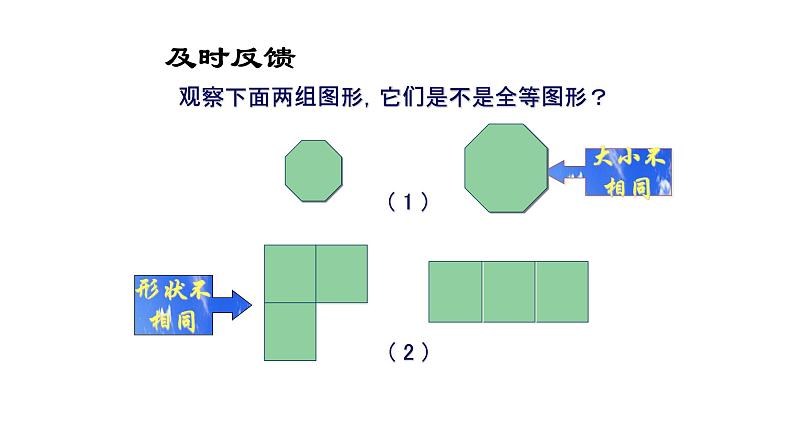
如果两个图形全等，它们的形状大小一定都相同吗？
全等图形的形状和大小都相同
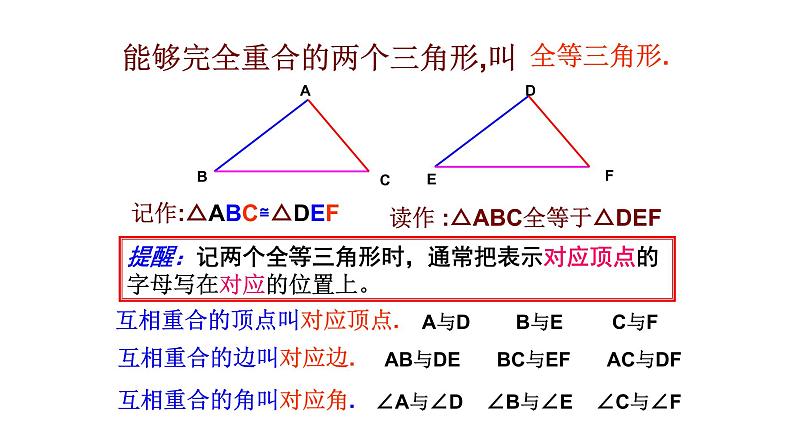
能够完全重合的两个三角形,叫
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
提醒：记两个全等三角形时，通常把表示对应顶点的字母写在对应的位置上。
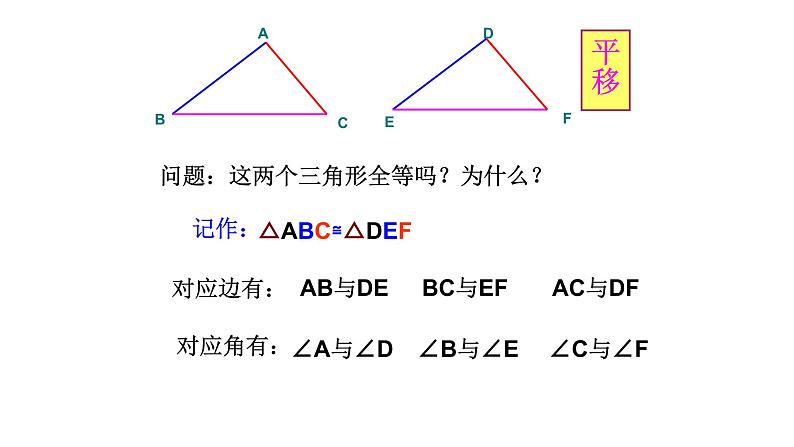
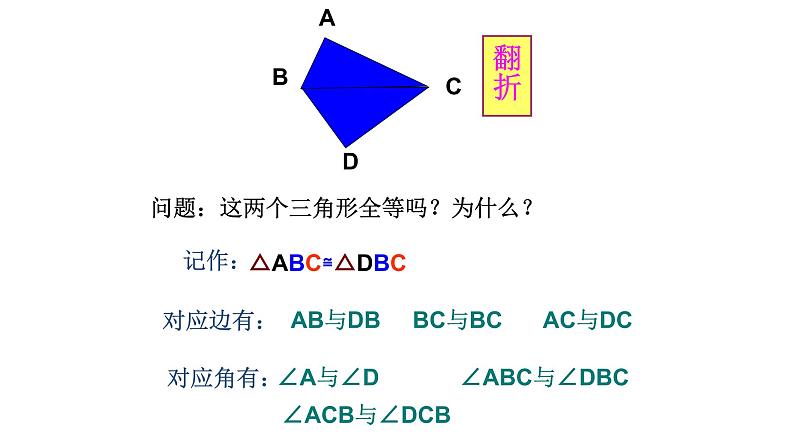
问题：这两个三角形全等吗？为什么？
思考：有那些办法可以验证两个三角形全等？
平移、翻折、旋转前后的图形全等。
找一找：请指出下列全等三角形的对应边和对应角
1、 △ ABE ≌ △ ACF
对应角是： ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC；对应边是AB和AC、AE和AF、BE和CF。
2、 △ BCE ≌ △ CBF
对应角是： ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是：CB和BC、CE和BF、CF和BE。
3、 △ BOF ≌ △ COE
从以上学习中你能总结出找全等三角形的对应边,对应角的规律吗?
1.有公共边的，公共边一定是对应边。
2.有对顶角的，对顶角一定是对应角
3.有公共角的，公共角一定是对应角。
4.对应角所对的边是对应边，对应边所对的角是对应角．
5.在两个全等三角形中最长边对最长边，最短边对最短边，最大角对最大角，最小角对最小角。
找全等三角形对应边、对应角的方法
1、大边对应大边，大角对应大角；
2、公共边是对应边，公共角是对应角；
3、对应边所对的角是对应角，对应角　　　　所对的边是对应边；
4、根据书写规范，按照对应顶点找对应边或对应角；
如图： △ABC≌△DEF
∴A B=D E，A C=D F，B C=EF（全等三角形对应边相等）
∠A=∠D，∠B=∠E，∠C=∠F（全等三角形的对应角相等）
强调：在表示全等三角形边、角相等时对应顶点写在对应位置上
全等三角形对应边相等；
全等三角形对应角相等；
例1：如图，△OCA≌△OBD，C和B，A和D是对应顶点，说出这两个三角形中相等的边和角。
解：相等的边有： AC=DB， AO=DO， CO=BO
相等的角有： ∠A= ∠D ∠C= ∠B ∠AOC= ∠DOB
△ADE≌△CBF。 AD=CB，DE=BF，AE=CF。∠ADE=∠CBF，∠AED=∠CFB，∠A=∠C。
△ABD≌△CDB。 AB=CD，AD=CB，BD=DB。∠ABD=∠CDB，∠ADB=∠CBD，∠A=∠C。
找出下列图中一对全等三角形，并写出相等 的边和相等的角。
△ABD≌△ACD。 AB=AC，BD=CD，AD=AD。∠ABD=∠ACD，∠ADB=∠ADC，∠BAD=∠CAD。
例2：如图△ABC≌ △ADE若∠D= ∠B， ∠C= ∠AED，则∠DAE= ； ∠DAB= 。
例4：如图△ ABD ≌ △CDB，若AB=4，AD=5，BD=6， ∠ABD=30°,则BC= ，CD=______, ∠CDB=____.
例 3： 如图已知△ AOC ≌ △BOD求证：AC∥BD
证明：∵ △ AOC ≌ △BOD
∴∠A=∠B（全等三角形对应角相等）
∴AC∥BD（内错角相等，两直线平行）
例4：如图，已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF
证明: ∵ΔABC≌ΔFED, BC=ED ∴BC与ED是对应边∴∠ =∠ , ( ) ∴ AB∥EF
将上述证明过程补充完整.
全等三角形的对应角相等
例7：如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C,请指出其余的对应边和对应角.
分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:∠ BAE与∠CAD是对应角,根据“对应角的对边是对应边 ”可知:AD与AE,AE与AD,BE与CD分别是对应边.
1、全等用符号 表示，读作： 。 2、若△ BCE ≌ △ CBF，则∠CBE= , ∠BEC= ,BE= , CE= . 3、判断题 1）全等三角形的对应边相等，对应角相等。（ 　） 2）全等三角形的周长相等，面积也相等。 （ 　） 3）面积相等的三角形是全等三角形。 （ 　） 4）周长相等的三角形是全等三角形。 （ 　 ）
如图:△ABC≌△DBF,找出图中的对应边,对应角.
答:∠B的对应角是( ) ∠C的对应角是( ) ∠BAC的对应角是( )
AB的对应边是( )AC的对应边是( )BC的对应边是( )
4、如图△ABD≌ △EBC，AB=3cm,BC=5cm,求DE的长
解：∵△ABD≌ △EBC∴AB=EB、BD=BC∵BD=DE+EB∴DE=BD-EB =BC-AB =5-3=2cm
下图是一个等边三角形，你能把它分成两个全等三角形吗？你能把它分成三个全等三角形吗？四个呢？