人教版数学8年级上册 第十二章 全等三角形 学案3

这是一份人教版数学8年级上册 第十二章 全等三角形 学案3，共5页。

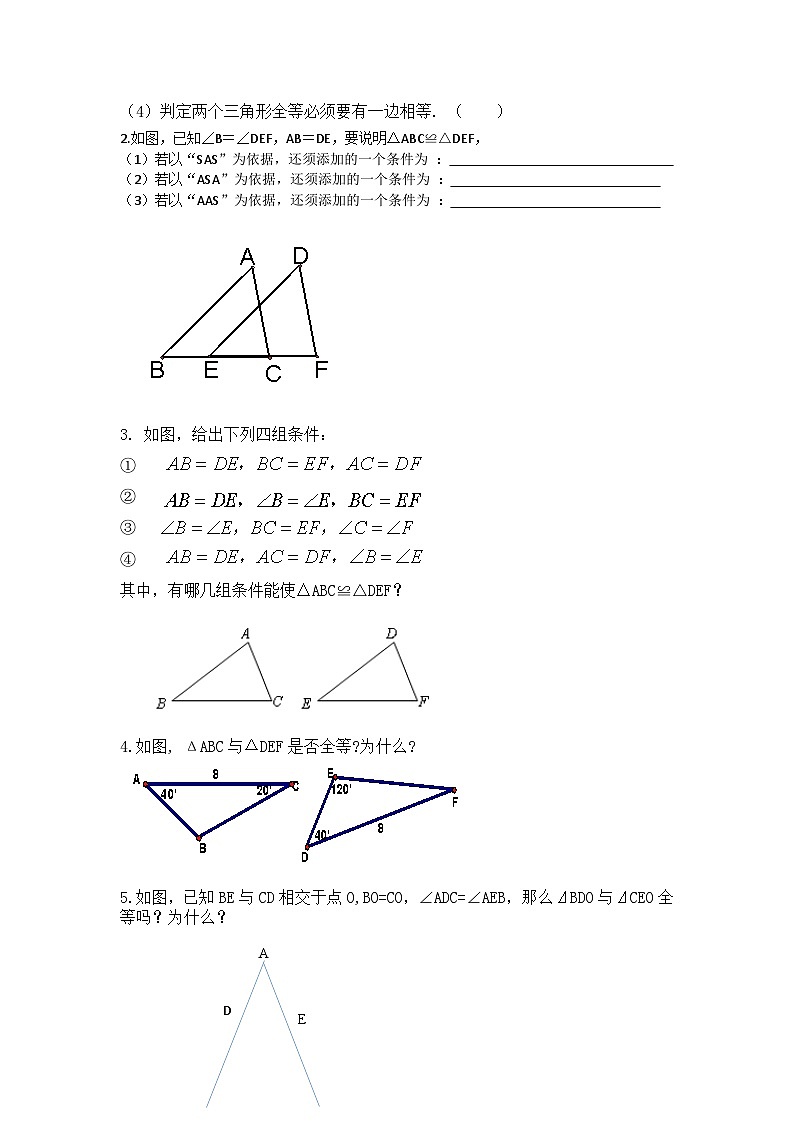
全等三角形教学目标：1、通过全等三角形的概念和识别方法的复习，让学生体会辨别、探寻、运用全等三角形的一般方法，体会主动实验，探究新知的方法。2、培养学生观察和理解能力，几何语言的叙述能力及运用全等知识解决实际问题的能力。3、在学生操作过程中，激发学生学习的兴趣，培养学生主动探索，敢于实践的精神，培养学生之间合作交流的习惯。教学的重点和难点：重点：运用全等三角形的识别方法来探寻三角形以及运用全等三角形的知识解决实际问题。难点：能准确地完成文字、数学语言与图形之间的转换，熟练掌握证明的一般步骤，准确地写出证明。教学过程：知识回顾判定三角形全等有哪些方法？SAS： 两条边及其夹角对应相等的两个三角形全等.ASA： 两个角及其夹边对应相等的两个三角形全等.AAS： 两个角及其其中一个角的对边对应相等的两个三角形全等.SSS： 三条边对应相等的两个三角形全等.注意：边边角（SSA）和角角角（AAA）是不能用的.全等三角形具有的性质：全等三角形对应边相等，对应角相等.知识运用1.判断下列命题的对错:（1）面积相等的两三角形一定全等. （ ）（2）有两边一角对应相等的两个三角形全等. （ ）（3）所有的等边三角形都全等.（ ）（4）判定两个三角形全等必须要有一边相等. （ ）2.如图，已知∠B＝∠DEF，AB＝DE，要说明△ABC≌△DEF，（1）若以“SAS”为依据，还须添加的一个条件为 ： （2）若以“ASA”为依据，还须添加的一个条件为 ： （3）若以“AAS”为依据，还须添加的一个条件为 ： 3. 如图，给出下列四组条件：① ② ③ ④ 其中，有哪几组条件能使△ABC≌△DEF？ 如图, ΔABC与ΔDEF是否全等?为什么? 5.如图，已知BE与CD相交于点O,BO=CO，∠ADC=∠AEB，那么⊿BDO与⊿CEO全等吗？为什么？AED CB 6. 如图，⊿ABC中，AB=AC，BD、CE分别是AC、AB边上的中线，BD、CE相交于点O，试说明OD=OE的理由.ADE CB 已知：AB=CD，AD=CB. 试说明∠A=∠C.CA DB 如图，已知，AB∥DE，AB=DE，AF=DC.问图中有那几对全等三角形？请任选一对给予证明. EFDACB9. 如图,已知AE⊥AB，AF⊥AC，AE=AB，AF=AC. 求证：（1）EC=BF；（2）EC⊥BFFCBEA课堂总结三角形全等解题的思路：（1）要说明边或角相等可证它们所在的三角形全等；（2）寻找可用的直接或间接的已知条件,选择判定全等的方法；（3）当条件不足时可根据已知条件先证另外两个三角形全等,再从中选择需要的对应角或对应边.2.三角形全等判定方法的选择：已知条件可选择的判定方法：两边对应相等：SAS、SSS两角对应相等：AAS、ASA一边一角对应相等：ASA、SAS，AAS3.说明三角形全等的注意事项:（1）所有全等的准备工作放在最前面写;（2）说明时注意三角形的对应顶点写在对应位置上;（3）大括号里按照所用判定的边角顺序写.四、课后作业1.配套练习题2.预习下一节课内容五、教学反思：本教学设计从以下三方面考虑：1、根据学生的学习情况，改进学生的学习方式，强调合作交流，探索学习，教师在教学过程中，努力为学生创设自主探索的氛围，让学生真正成为课堂主体。2、重视对学生能力的培养，除常规的鼓励就大胆思考，积极发言，重视培养学生观察、操作、测试、思考的能力，学生的活跃，他们思考问题的方式是多种多样，教师从对完全更改，尊重他们的学习方式，这样有助于创新3、重视对学生学习习惯的培养，全等三角形是几何部分内容说明书，有较强逻辑性，教师板演，以及在学生叙述中纠正学生的错误，是培养学生养成良好的习惯之一，同时学生学习习惯多方面的，在合作交流中，培养学生合作意识和合作习惯培养显得尤为重要。