








- 【同步学案】高中数学人教A版(2019)必修第一册--课时4.5 函数的应用(二)学案 3课时(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.1任意角和弧度制 学案 2课时(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.3 诱导公式 学案(Word版含答案) 学案 13 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.4 三角函数的图像与性质 学案(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.5 三角恒等变换 学案(Word版含答案) 学案 14 次下载
高中人教A版 (2019)5.2 三角函数的概念优质学案
展开![]() 课时5.2.2 同角三角函数的基本关系
课时5.2.2 同角三角函数的基本关系
01考点梳理
(1)平方关系:同一个角α的正弦、余弦的平方和等于 .即sin2α+cos2α= .
(2)商数关系:同一个角α的正弦、余弦的商等于这个角的 .即= .成立的角α的范围是.
答案:1 1 正切 ![]()
02考点解读
题型一 同角三角函数的基本关系
1.求下列三角方程的解集:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】(1)因为:![]() ;
;
所以:![]() ,
,![]() .
.
所以解集为:![]() .
.
(2)因为:![]() ,
,![]()
所以:![]()
![]() .
.
解得:![]() 或
或![]() (舍)
(舍)
所以解集为:![]() 或
或![]() .
.
(3)因为:![]()
所以:![]()
所以:![]() 或
或![]() .
.
所以解集为:![]() 或
或![]() .
.
(4)因为:![]() .且
.且![]() .
.
所以:![]() .
.
化简得:![]() .
.
解得:![]() 或
或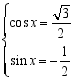 .
.
所以解集为:![]() 或
或![]() .
.
题型二 同角三角函数的基本关系求值
2.已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实根,且
的两个实根,且![]() ,则
,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】由![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实根,
的两个实根,
∴![]() ,解得
,解得![]() ,
,
又![]() ,则
,则![]() ,解得
,解得![]() ,则
,则![]() ,
,
∴![]() .
.
故答案为:![]()
题型三 三角函数的化简、求值
3.已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实根,且
的两个实根,且![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】由于![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实根,则
的两个实根,则![]() ,解得
,解得![]() .
.
![]() ,
,![]() .
.
而![]() ,所以
,所以![]() ,则
,则![]() ,可得
,可得![]() ,
,
![]() ,解得
,解得![]() ,
,
所以,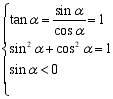 ,则
,则![]() ,因此,
,因此,![]() .
.
故答案为:![]() .
.
题型四 三角函数恒等式的证明
4.已知![]() ,求证:
,求证:![]() .
.
【答案】证明见解析
【解析】![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() 等式成立.
等式成立.
03题组训练
1.已知![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】∵![]() ,∴
,∴![]() .
.
∴![]()
故选:B
2.已知![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】∵![]() ,
,
∴![]() ,
,
∴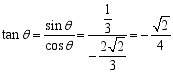 .
.
故选:D.
3.已知![]() 是第三象限角,且
是第三象限角,且![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】因为![]() 是第三象限角,所以
是第三象限角,所以![]() ,
,![]() ,故
,故![]() .
.
又因为![]() ,
,
所以![]() .故
.故![]() ,
,
所以![]() ,故选B.
,故选B.
4.已知![]() ,则
,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】因为![]() ,
,![]() ,所以
,所以![]() .
.
故选D
5.已知![]() ,且
,且![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】由![]() ,
,![]() 知
知![]() 是第三象限角,所以
是第三象限角,所以![]() ,
,
故![]()
![]()
![]() .
.
故答案为:![]() .
.
6.若![]() 为第三象限角,则
为第三象限角,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】∵![]() 为第三象限角,
为第三象限角,
∴![]() ,
,
∴原式![]() .
.
故答案为:![]() .
.
7.已知角![]() 的始边与
的始边与![]() 轴的非负半轴重合,顶点与坐标原点重合,终边过点
轴的非负半轴重合,顶点与坐标原点重合,终边过点![]() ,则
,则![]() ____.
____.
【答案】10
【解析】根据角![]() 的终边过
的终边过![]() ,利用三角函数的定义式,可以求得
,利用三角函数的定义式,可以求得![]()
所以有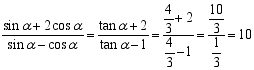 ,
,
故答案是10.
8.设![]() 且
且![]() ,若
,若![]() ,则
,则![]() ______.
______.
【答案】1
【解析】设![]() 且
且![]() ,若
,若![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
又由![]() ,
,
则![]()
所以![]()
![]()
故答案为1.
9.求证:![]() .
.
【答案】证明见解析
【解析】∵右边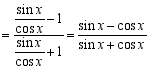 ,
,
左边![]()
![]()
![]() ,
,
∴左边=右边,故原等式成立.
10.已知![]() 求:
求:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】(1)![]()
![]() ,
,
即![]() ,
,
解得![]() 或
或![]() .
.
∵![]() ,
,
∴![]() 为第二象限角,
为第二象限角,
∴![]() ,∴
,∴![]() .
.
故答案为![]()
(2)原式![]() .
.
故答案为![]()
高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案: 这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案,文件包含同步学案高中数学人教版2019必修第一册--课时53考点诱导公式原卷版docx、同步学案高中数学人教版2019必修第一册--课时53考点诱导公式解析版docx等2份学案配套教学资源,其中学案共13页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数优秀学案设计: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数优秀学案设计,文件包含同步学案高中数学人教版2019必修第一册--课时432考点对数的运算原卷版docx、同步学案高中数学人教版2019必修第一册--课时431考点对数的概念原卷版docx、同步学案高中数学人教版2019必修第一册--课时432考点对数的运算解析版docx、同步学案高中数学人教版2019必修第一册--课时431考点对数的概念解析版docx等4份学案配套教学资源,其中学案共17页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.1 指数精品学案及答案: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.1 指数精品学案及答案,文件包含同步学案高中数学人教版2019必修第一册--课时421考点指数函数的概念原卷版docx、同步学案高中数学人教版2019必修第一册--课时422考点指数函数的图象和性质原卷版docx、同步学案高中数学人教版2019必修第一册--课时422考点指数函数的图象和性质解析版docx、同步学案高中数学人教版2019必修第一册--课时421考点指数函数的概念解析版docx等4份学案配套教学资源,其中学案共33页, 欢迎下载使用。













