














- 【同步学案】高中数学人教A版(2019)必修第一册--课时4.5 函数的应用(二)学案 3课时(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.1任意角和弧度制 学案 2课时(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.2 三角函数的概念 学案 2课时(Word版含答案) 学案 12 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.3 诱导公式 学案(Word版含答案) 学案 13 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时5.5 三角恒等变换 学案(Word版含答案) 学案 14 次下载
【同步学案】高中数学人教A版(2019)必修第一册--课时5.4 三角函数的图像与性质 学案(Word版含答案)
展开![]() 课时5.4.3 正切函数的性质与图象
课时5.4.3 正切函数的性质与图象
01考点梳理
一、正切函数的性质与图象
1.正切函数的性质
函数 | y=tan x,x∈R |
周期 | 最小正周期为 |
奇偶性 |
|
单调性 | 在每一个区间 上都 . |
值域 |
|
2.正切函数的图象
(1)正切函数的图象如右图所示.
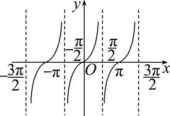
(2)正切函数的图象叫做 .
(3)正切函数的图象的特征:
正切曲线是被与y轴平行的一系列直线 所隔开的无穷多支形状相同的曲线组成的.
答案:π 奇函数 (-![]() +kπ,
+kπ,![]()
![]() +kπ)(k∈Z) 单调递增 R 正切曲线 x=
+kπ)(k∈Z) 单调递增 R 正切曲线 x=![]() +kπ,k∈Z
+kπ,k∈Z
02考点解读
题型一 正切函数的图象的应用
1.函数![]() 的图象可能是( )
的图象可能是( )
A.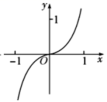 B.
B.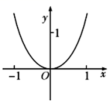
C.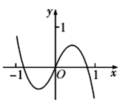 D.
D.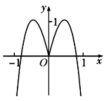
【答案】B
【解析】由![]()
![]() ,
,
则![]()
所以![]() ,即函数
,即函数![]() 是偶函数
是偶函数
故排除A,C,
当![]() 时,
时,![]() ,排除D.
,排除D.
故选:B
题型二 正切函数单调性的应用
2.直线![]() 与函数
与函数![]() 的图象的相邻两个交点的距离为
的图象的相邻两个交点的距离为![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】因为直线![]() 与函数
与函数![]() 的图象的相邻两个交点的距离为
的图象的相邻两个交点的距离为![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]()
由![]() 可得
可得![]()
当![]() 时可得
时可得![]() 在
在![]() 上单调递增
上单调递增
因为函数![]() 在区间
在区间![]() 上是增函数,所以实数
上是增函数,所以实数![]() 的取值范围是
的取值范围是![]()
故选:B
题型三 周期性与对称性
3.下列函数中,既是奇函数又以![]() 为最小正周期的函数是( )
为最小正周期的函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】解:A选项:![]() 是周期为
是周期为![]() 的偶函数,故A不正确;
的偶函数,故A不正确;
B选项:![]() 是周期为
是周期为![]() 的奇函数,故B正确;
的奇函数,故B正确;
C选项:![]() ,周期为
,周期为![]() 且非奇非偶函数,故C不正确;
且非奇非偶函数,故C不正确;
D选项:![]() 是周期为
是周期为![]() 的奇函数,故D不正确.
的奇函数,故D不正确.
故选:B.
题型四 正切函数的综合应用
4.函数![]() 在区间
在区间![]() 内的大致图象是下列图中的( )
内的大致图象是下列图中的( )
A.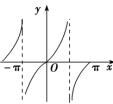 B.
B.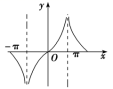
C.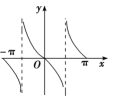 D.
D.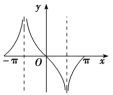
【答案】B
【解析】![]()
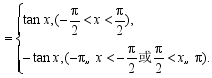
![]() 在
在![]() 上单调增,
上单调增,![]() 在
在![]() 上单调减.
上单调减.
03题组训练
1.函数![]() 在一个周期内的图象是( )
在一个周期内的图象是( )
A.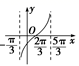 B.
B. C.
C.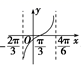 D.
D.
【答案】A
【解析】方法一:
由题意得函数的周期为![]() ,故可排除B,C,D.选A.
,故可排除B,C,D.选A.
方法二:
令![]() ,则有
,则有![]() ,故
,故![]() ,当k=0时,得
,当k=0时,得![]() ,可知函数图象与x轴一交点的横坐标为
,可知函数图象与x轴一交点的横坐标为![]() ,故可排除C、D.
,故可排除C、D.
令![]() ,得
,得![]() ,即函数图象的一条渐近线为
,即函数图象的一条渐近线为![]() ,故排除B.选A.
,故排除B.选A.
2.已知函数![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.函数![]() 的最小正周期为
的最小正周期为![]()
B.函数![]() 的值域为
的值域为![]()
C.点![]() 是函数
是函数![]() 的图像的一个对称中心
的图像的一个对称中心
D.![]()
【答案】D
【解析】因为![]() ,
,
所以函数![]() 的最小正周期
的最小正周期![]() ,故A正确.
,故A正确.
由正切函数的图像和性质可知函数![]() 的值域为
的值域为![]() ,故B正确.
,故B正确.
由![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
所以点![]() 是函数
是函数![]() 的图像的一个对称中心,故C正确.
的图像的一个对称中心,故C正确.
因为![]() ,
,
![]() ,
,
所以![]() ,故D不正确.
,故D不正确.
故选:D.
3.不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】![]()
当![]() 时,
时,
![]() ,
,![]()
且![]() 单调递增,
单调递增,
所以![]() ,
,
因为![]() 的周期为
的周期为![]() ,
,
所以不等式的解集为![]() .
.
故选:A.
4.已知函数![]() (
(![]() )的图象的相邻两支截直线
)的图象的相邻两支截直线![]() 所得线段长为
所得线段长为![]() ,则
,则![]() 的值是
的值是
A.0 B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】由题意,可知![]() ,所以
,所以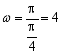 ,即
,即![]() ,
,
所以![]() ,
,
故选:A
5.函数![]() (
(![]() 且
且![]() )的值域为
)的值域为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】试题分析:![]() 且
且![]() ,
,![]() 且
且![]() ,
,
由于正切函数的图象及单调性,得:
![]() 或
或![]() ,
,
即![]()
故选B.
6.已知函数![]() ,
,![]() 的部分图像如下图,则
的部分图像如下图,则![]() =____________.
=____________.
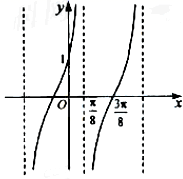
【答案】![]()
【解析】由题意![]() ,∴
,∴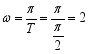 ,
,
又![]() ,
,![]() ,而
,而![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为![]() .
.
7.关于函数![]() ,有以下命题:
,有以下命题:
①函数![]() 的定义域是
的定义域是![]()
②函数![]() 是奇函数;
是奇函数;
③函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④函数![]() 的一个单调递增区间为
的一个单调递增区间为![]() .
.
其中,正确的命题序号是______________.
【答案】①③
【解析】
对于①,由![]() 有
有![]() ,所以①是正确的;对于②,由于函数
,所以①是正确的;对于②,由于函数![]() 的定义域不是关于原点对称,所以函数
的定义域不是关于原点对称,所以函数![]() 是非奇非偶函数,②错误;对于③,由于
是非奇非偶函数,②错误;对于③,由于![]() ,所以函数
,所以函数![]() 的图象关于点
的图象关于点![]() 对称;对于④,令
对称;对于④,令![]() ,解得
,解得![]() ,故单调递增区间为
,故单调递增区间为![]() ,所以④是错误的.本题正确答案为①,③.
,所以④是错误的.本题正确答案为①,③.
8.若函数![]() 在区间
在区间![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】因为函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴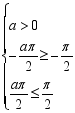 ,解得
,解得![]()
故答案为![]()
9.已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)用定义判断函数![]() 的奇偶性;
的奇偶性;
(3)在![]() 上作出函数
上作出函数![]() 的图象.
的图象.
【答案】(1)![]() ;(2)奇函数,见解析;(3)见解析
;(2)奇函数,见解析;(3)见解析
【解析】(1)由![]() ,得
,得![]() (
(![]() ),
),
所以函数![]() 的定义域是
的定义域是![]() .
.
(2)由(1)知函数![]() 的定义域关于原点对称,
的定义域关于原点对称,
因为![]() ,所以
,所以![]() 是奇函数.
是奇函数.
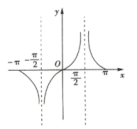
(3)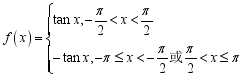 ,
,
所以![]() 在
在![]() 上的图象如图所示,
上的图象如图所示,
10.已知![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)求![]() 的取值范围,使
的取值范围,使![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)当![]() 时,
时,![]() ,
,![]() ,
,
根据二次函数的性质可得:当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;
;
(2)函数![]() 图象的对称轴为
图象的对称轴为![]() ,
,
∵![]() 在
在![]() 上是单调函数,
上是单调函数,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
因此,![]() 角的取值范围是
角的取值范围是![]() .
.
高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案: 这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案,文件包含同步学案高中数学人教版2019必修第一册--课时53考点诱导公式原卷版docx、同步学案高中数学人教版2019必修第一册--课时53考点诱导公式解析版docx等2份学案配套教学资源,其中学案共13页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.3 对数优秀学案: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数优秀学案,文件包含同步学案高中数学人教版2019必修第一册--课时441考点对数函数的概念原卷版docx、同步学案高中数学人教版2019必修第一册--课时442考点对数函数的图象和性质原卷版docx、同步学案高中数学人教版2019必修第一册--课时443考点不同函数增长的差异原卷版docx、同步学案高中数学人教版2019必修第一册--课时441考点对数函数的概念解析版docx、同步学案高中数学人教版2019必修第一册--课时442考点对数函数的图象和性质解析版docx、同步学案高中数学人教版2019必修第一册--课时443考点不同函数增长的差异解析版docx等6份学案配套教学资源,其中学案共37页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数优秀学案设计: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数优秀学案设计,文件包含同步学案高中数学人教版2019必修第一册--课时432考点对数的运算原卷版docx、同步学案高中数学人教版2019必修第一册--课时431考点对数的概念原卷版docx、同步学案高中数学人教版2019必修第一册--课时432考点对数的运算解析版docx、同步学案高中数学人教版2019必修第一册--课时431考点对数的概念解析版docx等4份学案配套教学资源,其中学案共17页, 欢迎下载使用。













