人教版八年级数学上册单元检测 第十二章

第十二章

一、选择题(每题3分，共30分)

1．如图，有四张小画片，画的都是人物图形，与另外三张与众不同的是(　　)

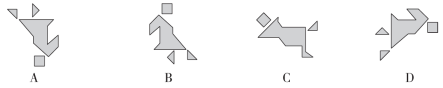
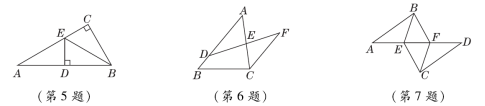
2．【2023·北京四中月考】如图，△ACE≌△DBF，CD＝3，BC＝2，则AC＝(　　)

A．2  B．8  C．5  D．3

3．如图，已知AB＝DC，∠ABC＝∠DCB，能直接判定△ABC≌△DCB的方法是(　　)

A．SAS  B．AAS  C．SSS  D．ASA

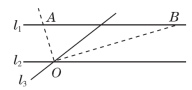
4．【母题：教材P50练习T1】如图，l3与两条平行公路l1，l2三条公路相交，若要在l1上确定某个位置，使其到另两条公路的距离相等，这样的位置有(　　)

A．1个  B．2个  C．3个  D．无数个

5．如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D，如果

AE＋DE＝3 cm，那么AC等于(　　)

A．5 cm  B．2 cm  C．4 cm  D．3 cm

6．【母题：教材P45习题T12】如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若AB＝4，CF＝3，则BD的长是(　　)

A．0.5  B．1  C．1.5  D．2

7．如图，已知AB∥CD，AB＝CD，AE＝FD，则图中的全等三角形有(　　)

A．1对  B．2对  C．3对  D．4对

8．如图，CA平分∠DCB，CB＝CD，DA的延长线交BC于点E，若∠EAC＝48°，则∠BAE的度数为(　　)

A．84°  B．90°  C．88°  D．96°

9．【2023·天津天大附中月考】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为27和16，则△EDF的面积为(　　)

A．11  B．5.5  C．7  D．3.5

10．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°.连接AC，BD交于点M，连接OM.下列结论：

①∠AMB＝36°；②AC＝BD；③OM平分∠AOD；④MO平分∠AMD.

其中正确结论的个数是(　　)

A．4  B．3  C．2  D．1

二、填空题(每题3分，共24分)

11．如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________．

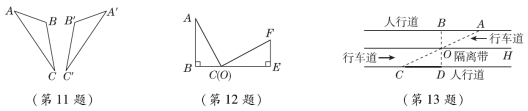
12．【开放性题】 如图，B，C(O)，E四点在同一条直线上，∠B＝∠E＝90°，AB＝CE，请添加一个适当的条件：________，使得△ABC≌△OEF(只需写一个，不添加辅助线)．

13．为迎接某次活动，我校举行“缓堵保畅，安全出行，小手拉大手活动”．每天值班老师和部分学生在校门两边站岗执勤(线段CD所在区域)．如图，AB∥OH∥CD，AC与BD相交于O，OD⊥CD于点D，OD＝OB，已知AB＝300米，请根据上述信息求出执勤区域CD的长度是________．

14．【母题：教材P56复习题T12】如图，在Rt△ABC中，∠C＝90°，AM是∠CAB的平分线，CM＝1.5 cm，若AB＝6 cm，则S△AMB＝________cm2.

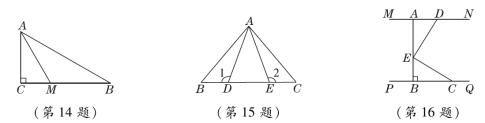
15．如图，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAC＝80°，则∠CAE的度数是________．

16．如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，点E在AB上，AD＋BC＝7，AD＝BE，DE＝EC，则AB＝________．

17．如图，已知AB＝20米，MA⊥AB于A，MA＝10米，射线BD⊥AB于B，P点从B点向A点运动，每秒走2米，Q点从B点出发沿BD运动，每秒走3米，P，Q同时从B出发，则出发________秒后，在线段MA上有一点C，使△CAP与△PBQ全等．

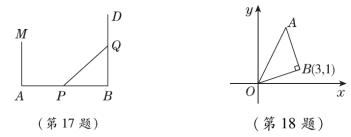
18．【2023·重庆一中模拟】如图，在平面直角坐标系中，点B的坐标为(3，1)，

AB＝OB，∠ABO＝90°，则点A的坐标是____________．

三、解答题(19～21题每题10分，其余每题12分，共66分)

19．如图①，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞，油纸伞的制作工艺十分巧妙，如图②，伞圈D沿着伞柄AP滑动时，总有伞骨

BD＝CD，AB＝AC，从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC，请你说明其中的理由．

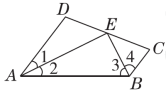
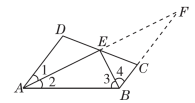
20．【母题：教材P52习题T7】如图，AD∥BC，∠1＝∠2，∠3＝∠4，直线DC过点E交AD于点D，交BC于点C.求证：E为CD的中点．(温馨提示：延长AE交BC的延长线于点F)

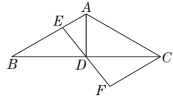
21．如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F.

 (1)求证：△BDE≌△CDF；

(2)当AD⊥BC，AE＝1，CF＝2时，求AC的长．

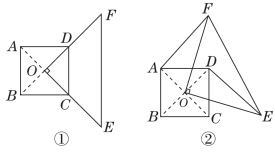
22．如图①，等腰直角三角形OEF的直角顶点O为正方形ABCD的中心，点C，D分别在OE和OF上．现将△OEF绕点O逆时针旋转α(0°<α<90°)，连接AF，DE，如图②.

(1)在图②中，∠AOF＝__________(用含α的式子表示)；

(2)在图②中，猜想AF与DE的数量关系，并证明你的结论．

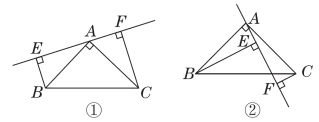
23．如图，在△ABC中，AB＝AC，∠BAC＝90°，分别过点B，C向过点A的直线作垂线，垂足分别为点E，F.

(1)如图①，过点A的直线与斜边BC不相交时，求证：①△ABE≌△CAF；②EF＝BE＋CF.

(2)如图②，其他条件不变，过点A的直线与斜边BC相交时，若BE＝10，CF＝3，试求EF的长．

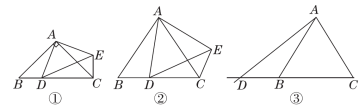
24．在△ABC中，AB＝AC，点D是射线CB上的一动点(不与点B，C重合)，以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE.

(1)如图①，当点D在线段CB上，∠BAC＝90°时，那么∠DCE＝________°；

(2)设∠BAC＝α，∠DCE＝β.

①如图②，当点D在线段CB上，∠BAC≠90°时，请你探究α与β之间的数量关系，并证明你的结论；

②如图③，当点D在线段CB的延长线上，∠BAC≠90°时，请将图③补充完整，并直接写出此时α与β之间的数量关系(不需证明)．

答案

一、1.C　2.C　3.A

4．B　【点拨】作直线l2与l3夹角的平分线OA，OB，交直线l1于A，B两点，如图，则在l1上到另两条公路的距离相等的位置有点A和点B两个位置，故选B.

5．D　6.B　7.C　8.A

9．B　【点拨】过D点作DH⊥AC于H，先根据角平分线的性质得到DF＝DH，再证明Rt△ADF≌Rt△ADH，得到S△ADF＝S△ADH.通过证明Rt△EDF≌Rt△GDH得到S△EDF＝S△GDH，然后利用S△EDF＋S△AED＝S△ADG－S△GDH得到S△EDF＋16＝27－S△EDF，从而可求出S△EDF的值．

10．B　【点拨】∵∠AOB＝∠COD＝36°，

∴∠AOB＋∠BOC＝∠COD＋∠BOC，

即∠AOC＝∠BOD.

在△AOC和△BOD中，

∴△AOC≌△BOD(SAS)．

∴∠OAC＝∠OBD，AC＝BD，故②正确．

又∵由三角形内角和定理得∠AMB＋∠OBD＝∠OAC＋∠AOB，

∴∠AMB＝∠AOB＝36°，故①正确．

作OG⊥AM于点G，OH⊥DM于点H，如图所示，

则∠OGA＝∠OHB＝90°.

∵△AOC≌△BOD，

∴OG＝OH.

∴MO平分∠AMD，故④正确．

假设OM平分∠AOD，则∠DOM＝∠AOM.　

在△AMO和△DMO中，

∴△AMO≌△DMO(ASA)．∴AO＝OD.

∵OC＝OD，∴OA＝OC.与OA＜OC矛盾，故③错误．

正确的个数有3个，故选B.

二、11.120°

12．AC＝OF(答案不唯一)

13．300米　【点拨】由AB∥CD，利用平行线的性质可得∠ABO＝∠CDO，结合OD＝OB，∠AOB＝∠COD，利用ASA定理可得△ABO≌△CDO，由全等三角形的性质可得区域CD的长度．

14．4.5　15.20°　16.7

17．4　【点拨】分两种情况考虑：当△APC≌△BQP时与当△APC≌△BPQ时，根据全等三角形的性质即可确定出时间．

18．(2，4)　【点拨】解本题的关键是过点A，B分别作x轴、y轴的平行线，构造长方形．在平面直角坐标系中求点的坐标就是求该点到两坐标轴的距离，从而转化为求线段长，而全等三角形的对应边相等，为求线段长提供了重要的依据．

三、19.【解】在△ABD和△ACD中，

∴△ABD≌△ACD(SSS)，

∴∠BAD＝∠CAD.即AP平分∠BAC.

20．【证明】如图，延长AE交BC的延长线于点F.

∵AD∥BC，

∴∠1＝∠F.

∵∠1＝∠2，

∴∠2＝∠F.

在△AEB和△FEB中，

∴△AEB≌△FEB(AAS)．

∴AE＝FE.

在△DAE和△CFE中，

∴△DAE≌△CFE(ASA)．

∴DE＝CE，即E为CD的中点．

21．(1)【证明】∵CF∥AB，

∴∠B＝∠FCD，∠BED＝∠F.

∵AD是BC边上的中线，∴BD＝CD.

∴△BDE≌△CDF(AAS)．

(2)【解】∵△BDE≌△CDF，

∴BE＝CF＝2.

∴AB＝AE＋BE＝1＋2＝3.

∵AD⊥BC，∴∠ADB＝∠ADC＝90°.

又∵BD＝CD，AD＝AD，

∴△ABD≌△ACD(SAS)．

∴AC＝AB＝3.

22．【解】(1)90°－α

(2)AF＝DE.

证明：∵四边形ABCD是正方形，

∴OA＝OD，∠AOD＝∠COD＝90°.

由旋转可知∠DOF＝∠COE，

∴∠AOD－∠DOF＝∠COD－∠COE，

即∠AOF＝∠DOE.

又∵OE＝OF，

∴△AOF≌△DOE(SAS)．

∴AF＝DE.

23．(1)【证明】①∵BE⊥EF，CF⊥EF，

∴∠AEB＝∠CFA＝90°.

∴∠EAB＋∠EBA＝90°.

∵∠BAC＝90°，

∴∠EAB＋∠FAC＝90°.∴∠EBA＝∠FAC.

在△ABE和△CAF中，

∴△ABE≌△CAF(AAS)．

②由①知△ABE≌△CAF，∴AE＝CF，BE＝AF.

∴EF＝AF＋AE＝BE＋CF.

(2)【解】∵BE⊥AF，CF⊥AF，

∴∠AEB＝∠CFA＝90°.

∴∠EAB＋∠EBA＝90°.

∵∠BAC＝90°，

∴∠EAB＋∠FAC＝90°.

∴∠EBA＝∠FAC.

在△ABE和△CAF中，

∴△ABE≌△CAF(AAS)．

∴AE＝CF，BE＝AF.

∴EF＝AF－AE＝BE－CF＝10－3＝7.

24．【解】(1)90

(2)①α＋β＝180°.

证明：∵∠BAC＝∠DAE，

∴∠BAC－∠DAC＝∠DAE－∠DAC，

即∠BAD＝∠CAE.

在△BAD和△CAE中，

∴△BAD≌△CAE(SAS)．∴∠B＝∠ACE.

∵∠B＋∠ACB＝180°－α，

∴∠DCE＝∠ACE＋∠ACB＝∠B＋∠ACB＝180°－α＝β.

∴α＋β＝180°.

②如图所示．

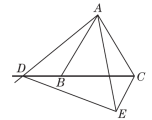
α＝β.