人教版八年级数学上册单元检测 第十一章

这是一份人教版八年级数学上册单元检测 第十一章，共12页。
第十一章一、选择题(每题3分，共30分)1．下面各项都是由三条线段组成的图形，其中属于三角形的是(　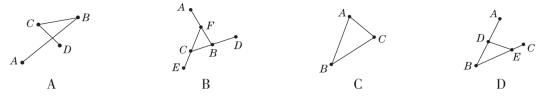　)2．【2023·石家庄四十三中模拟】下列图形中，是直角三角形的是(　　)3．【2022·临沂】如图是某一水塘边的警示牌，牌面是五边形，这个五边形的内角和是(　　)A．900°  B．720°  C．540°  D．360°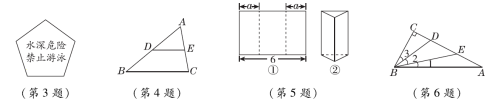4．如图，在△ABC中，若∠A＝60°，∠B＝40°，DE∥BC，则∠AED的度数是(　　)A．50°  B．60°  C．70°  D．80°5．【2022·益阳】如图①，将长为6的长方形纸片沿虚线折成3个长方形，其中左右两侧长方形的宽相等，若要将其围成如图②所示的三棱柱形物体，则图中a的值可以是(　　)A．1  B．2  C．3  D．46．如图，在△ABC中，∠C＝90°，D，E是AC上两点，且AE＝DE，BD平分∠EBC，那么下列说法中不正确的是(　　)A．BE是△ABD的中线  B．BD是△BCE的角平分线C．∠1＝∠2＝∠3  D．BC是△ABE的高7．【母题：教材P25习题T6】如果一个多边形的内角和是外角和的5倍，那么这个多边形的边数是(　　)A．10  B．11  C．12  D．138．将一副直角三角尺按如图所示的方式放置，使含30°角的三角尺的直角边和含45°角的三角尺的直角边垂直，则∠1的度数为(　　)A．45°  B．60°  C．70°  D．75°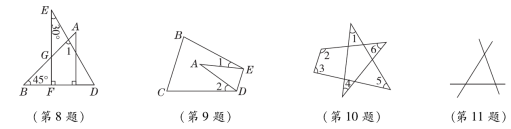9．如图，把三角形纸片ABC沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1＋∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，这个规律是(　　)A．∠A＝∠1＋∠2    B．2∠A＝∠1＋∠2C．3∠A＝2∠1＋∠2  D．3∠A＝2(∠1＋∠2)10．如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝(　　)A．180°  B．360°  C．540°  D．720°二、填空题(每题3分，共24分)11．【数学文化】花楼提花机是我国古代织造技术最高成就的代表，明代《天工开物》中详细记载了花楼提花机的构造．如图是提花机上的一个三角形木框架，它是由三根木料固定而成，三角形的大小和形状固定不变，三角形的这个性质叫做三角形的____________．12．如图，平面内有五个点，以其中任意三个点为顶点画三角形，最多可以画________个三角形．13．【2023·北大附中模拟】三个数3，1－a，1－2a对应的点在数轴上从左到右依次排列，且以这三个数为边长能构成三角形，则a的取值范围为________．14．如图是一台起重机的工作简图，前后两次吊杆位置OP1，OP2与吊绳的夹角分别是30°和70°，则吊杆前后两次的夹角∠P1OP2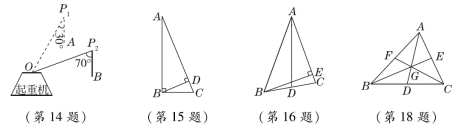＝________.15．如图，在Rt△ABC中，∠ABC＝90°，AB＝12 cm，BC＝5 cm，AC＝13 cm，若BD是AC边上的高，则BD的长为________cm.16．【母题：教材P29复习题T8】如图，AD是△ABC的角平分线，BE是△ABC的高，∠BAC＝40°，且∠ABC与∠ACB的度数之比为34，则∠ADC＝________，∠CBE＝________．17．【母题：教材P28复习题T4】如果从一个多边形的一个顶点出发可以画7条对角线，那么这个多边形的内角和为________．18．【2022·荆门】如图，点G为△ABC的重心，D，E，F分别为BC，CA，AB的中点，具有性质：AG∶GD＝BG∶GE＝CG∶GF＝2∶1.已知△AFG的面积为3，则△ABC的面积为________．三、解答题(19～21题每题8分，22～24题每题10分，25题12分，共66分)19．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，求∠ECD的度数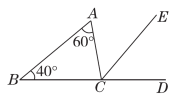．       20．如图，已知AD是△ABC的边BC上的中线．(1)作出△ABD的边BD上的高；(2)若△ABD的面积为6，且BD边上的高为3，求BC的长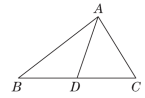．    21．【2023·天津南开中学月考】已知a，b，c是△ABC的三边长．(1)若a，b，c满足|a－b|＋(b－c)2＝0，试判断△ABC的形状；(2)若a，b，c满足(a－b)(b－c)＝0，试判断△ABC的形状；(3)化简：|a－b－c|＋|b－c－a|＋|c－a－b|.    22．如图，在△ABC中，BD是AC边上的高，∠A＝70°.(1)求∠ABD的度数；(2)若CE平分∠ACB交BD于点E，∠BEC＝118°，求∠ABC的度数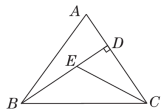．    23．【母题：教材P25习题T10】如图，六边形ABCDEF的内角都相等，CF∥AB.(1)求∠FCD的度数；(2)求证：AF∥CD. 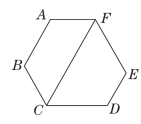   24．如图①，线段AB与CD相交于点O，连接AD，CB.如图②，在图①的条件下，∠DAB的平分线AP和∠BCD的平分线CP相交于点P，并且AP交CD于点M，CP交AB于点N，试解答下列问题：(1)在图①中，∠A，∠B，∠C，∠D之间的数量关系为______________________；(2)在图②中，若∠D＝42°，∠B＝38°，试求∠P的度数．     25．已知∠MON＝40°，OE平分∠MON，点A，B，C分别是射线OM，OE，ON上的动点(A，B，C不与点O重合)，连接AC交射线OE于点D.设∠OAC＝x°.(1)如图①，若AB∥ON，则①∠ABO的度数是________．②当∠BAD＝∠ABD时，x＝________；当∠BAD＝∠BDA时，x＝________．(2)如图②，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．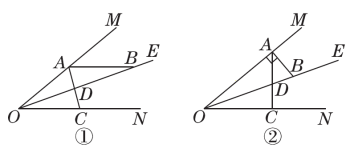  
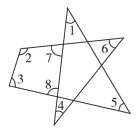
答案一、1.C　2.B　3.C　4.D5．B　　【点拨】由题意得解得＜a＜3.在1，2，3，4中，只有2符合上面不等式组的解集，∴a的值可以是2.6．C　7.C8．D　【点拨】由题意可得∠B＝45°，∠E＝30°，∠EFD＝90°，利用三角形的外角的性质及对顶角的性质可求出∠AGE的度数，再利用三角形外角的性质可求出∠1的度数．9．B　【点拨】根据三角形的内角和为180°以及四边形的内角和为360°得到几个角之间的等量关系，整理化简即可得到所求角之间的关系．10．B　【点拨】如图， ∵∠1＋∠5＝∠8，∠4＋∠6＝∠7，∠2＋∠3＋∠7＋∠8＝360°，∴∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝360°.二、11.稳定性12．10　【点拨】如图所示，以A，B为顶点，得△ABC，△ABD，△ABE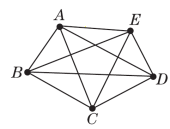，以A，C为顶点，得△ACD，△ACE，以A，D为顶点，得△ADE，以B，C为顶点，得△BCE，△BCD，以B，D为顶点，得△BDE，以C，D为顶点，得△CDE.故以其中任意三个点为顶点画三角形，最多可以画10个三角形．13．－3<a<－214．40°　【点拨】延长P1A交OP2于点C.根据题意可得P1A∥P2B，∠P1＝30°，∠P2＝70°，由两直线平行，内错角相等，可求得∠P1CP2的度数，由三角形外角的性质，即可求得吊杆前后两次的夹角∠P1OP2的度数．15．16．80°；10°　【点拨】∵△ABC中，∠BAC＋∠ABC＋∠ACB＝180°，∠BAC＝40°，∴∠ABC＋ ∠ACB＝140°.∵∠ABC与∠ACB的度数之比为34，∴设∠ABC＝3x，则∠ACB＝4x，∴3x＋4x＝140°，解得x＝20°，∴∠ABC＝60°， ∠ACB＝80°.∵AD是△ABC的角平分线，∠BAC＝40°，∴∠BAD＝∠CAD＝20°.∵∠ADC＝∠BAD＋∠ABD，∴∠ADC＝80°.∵BE是△ABC的高，∴∠BEC＝90°，∴∠ACB＋∠CBE＝90°，∴∠CBE＝10°.17．1 440°　【点拨】从一个多边形的一个顶点出发可以画7条对角线，则这个多边形的边数是10，代入多边形内角和公式即可求出答案．18．18　【点拨】∵CGGF＝21，△AFG的面积为3，∴△ACG的面积为6，∴△ACF的面积为3＋6＝9.∵点F为AB的中点，∴△ACF的面积＝△BCF的面积，∴△ABC的面积为9＋9＝18.三、19.【解】∵∠A＝60°，∠B＝40°，∴∠ACD＝∠A＋∠B＝100°.∵CE平分∠ACD，∴∠ECD＝∠ACD＝50°.20．【解】(1)如图，AM为△ABD的边BD上的高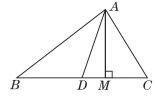．(2)∵△ABD的面积为6，BD边上的高为3，∴BD＝6×2÷3＝4.又∵AD是△ABC的边BC上的中线，∴BC＝2BD＝8.21．【解】(1)∵|a－b|＋(b－c)2＝0，∴a－b＝0且b－c＝0.∴a＝b＝c.∴△ABC为等边三角形．(2)∵(a－b)(b－c)＝0，∴a－b＝0或b－c＝0.∴a＝b或b＝c.∴△ABC为等腰三角形．(3)∵a，b，c是△ABC的三边长，∴a－b－c＜0，b－c－a＜0，c－a－b＜0.∴原式＝－a＋b＋c－b＋c＋a－c＋a＋b＝a＋b＋c.22．【解】(1)在△ABC中，∵BD是AC边上的高，∴∠ADB＝∠BDC＝90°.又∵∠A＝70°，∴∠ABD＝180°－∠ADB－∠A＝180°－90°－70°＝20°.(2)∵∠BEC＝∠BDC＋∠DCE，∠BEC＝118°，∠BDC＝90°，∴∠DCE＝28°.又∵CE平分∠ACB，∴∠DCB＝2∠DCE＝2×28°＝56°.∴∠DBC＝180°－∠BDC－∠DCB＝180°－90°－56°＝34°.∴∠ABC＝∠ABD＋∠DBC＝20°＋34°＝54°.23．(1)【解】∵六边形ABCDEF的内角都相等，内角和为(6－2)×180°＝720°，∴∠B＝∠A＝∠BCD＝720°÷6＝120°.∵CF∥AB，∴∠B＋∠BCF＝180°.∴∠BCF＝60°.∴∠FCD＝∠BCD－∠BCF＝60°.(2)【证明】∵CF∥AB，∴∠A＋∠AFC＝180°.∵∠A＝120°，∴∠AFC＝180°－120°＝60°.∴∠AFC＝∠FCD.∴AF∥CD.24．【解】(1)∠A＋∠D＝∠B＋∠C(2)根据(1)可知，∠1＋∠2＋∠D＝∠3＋∠4＋∠B，∠1＋∠D＝∠3＋∠P.∴2∠1＋2∠D＝2∠3＋2∠P.∵AP，CP分别是∠DAB和∠BCD的平分线，∴∠1＝∠2，∠3＝∠4.∴2∠1＋∠D＝2∠3＋∠B.∴2∠P＝∠B＋∠D.∴∠P＝(∠B＋∠D)＝×(38°＋42°)＝40°.25．【解】(1)①20°　②120；60(2)①当点D在线段OB上时，若∠BAD＝∠ABD，则x＝20.若∠BAD＝∠BDA，则x＝35.若∠ADB＝∠ABD，则x＝50.②当点D在射线BE上时，由题易知∠ABE＝110°，因为三角形的内角和为180°，所以只有∠BAD＝∠BDA，此时x＝125.综上可知，存在这样的x的值，使得△ADB中有两个相等的角，且x＝20，35，50或125.