



初中数学苏科版八年级上册4.3 实数优秀课件ppt
展开什么是有理数?有理数怎样分类?
第1课时 实数及其分类
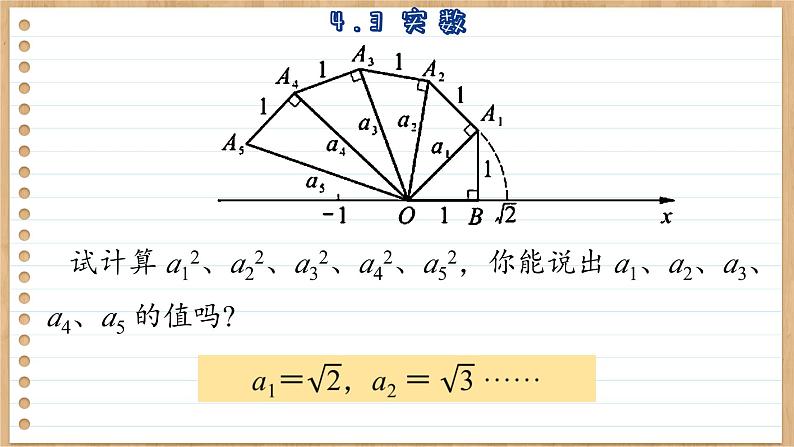
1. 如图 4-3,OB=BA1=A1A2=A2A3=A3A4 =A4A5=··· =1,∠A1BO=∠A2A1O=∠A3A2O=∠A4A3O=∠A5A4O=···=90°.
试计算 a12、a22、a32、a42、a52,你能说出 a1、a2、a3、a4、a5 的值吗?
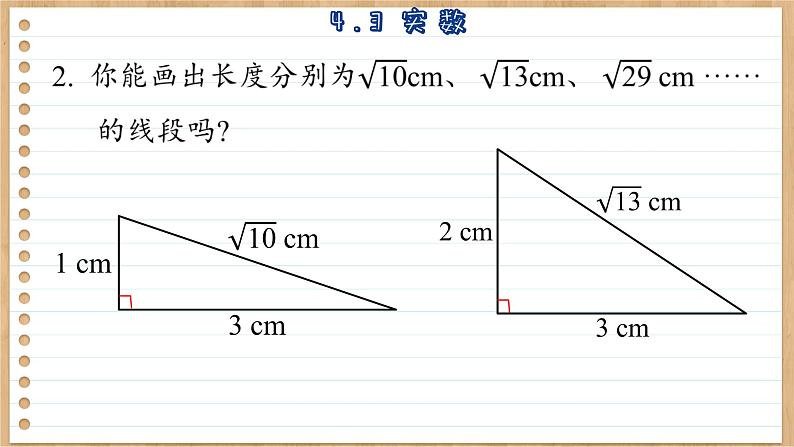
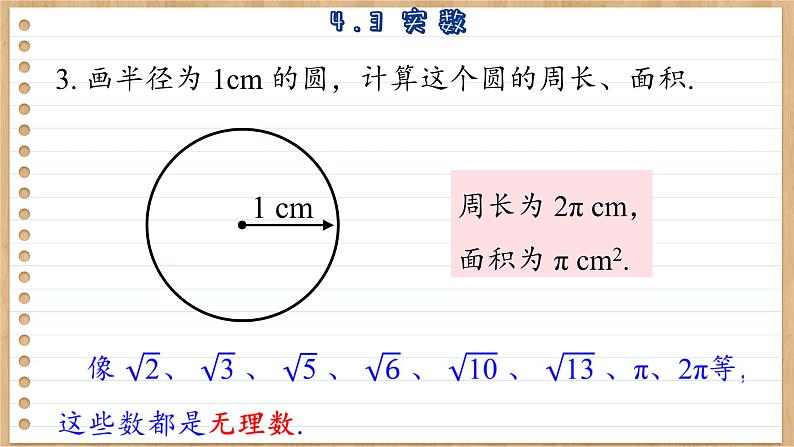
3. 画半径为 1cm 的圆,计算这个圆的周长、面积.
周长为 2π cm,面积为 π cm2.
知识点 1 无理数
无限不循环小数叫做无理数.
小数位数无限,小数形式为不循环.
(1) 无理数都是无限小数,但无限小数不一定是无理数; (2) 带根号的数不一定都是无理数,不带根号的数也不一定就是有理数.
知识点 2 实 数
有理数和无理数统称为实数.
有理数集合:{ … } ;无理数集合:{ … } ;整数集合:{ … } ; 分数集合:{ … } ;正实数集合:{ … } ;负实数集合:{ … }
知识点 3 实 数与数轴
每一个实数都可以用数轴上的一个点来表示; 反过来,数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应.
可用两点所表示的实数来表示,即点A、点B 在数轴上表示的实数分别为x1、x2, 则 AB= |x1-x2| .
(1) 有理数:{ ···};(2) 无理数:{ ···};(3) 正实数:{ ···};(4) 负实数:{ ···};
1、无限不循环的小数 叫做无理数. 有理数和无理数统称实数.
2、实数与数轴上的点是一一对应的.
3、同样的,平面直角坐标系中的点与有序实数对是 一一对应的.
第2课时 实数的性质
有理数的绝对值、相反数、倒数的意义,有理数大小比较的方法有理数的运算性质、运算律,在实数范围内都仍然适用. 在实数范围内,不仅可以进行加、减、乘、除、乘方运算,而且可以进行开立方运算以及非负实数的开平方运算.
知识点 4 实数的性质
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.(2) 对实数的有关概念进行辨析时,错误的说法只需举一个反例即可.
(1) 定义法:正数大于0,负数小于0, 正数大于一切负数;(2) 性质法:两个正数, 绝对值大的数大; 两个负数,绝对值大的数反而小.
相反数:倒数:绝对值:
知识点 5 实数的运算
1. 在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
2. 实数的运算律 加法交换律:a+b=b+a; 加法结合律:(a+b)+c=a+(b+c); 乘法交换律:ab=ba; 乘法结合律:(ab)c=a(bc); 乘法分配律:(a+b)c=ac+bc.
例2 用计算器计算:
≈ - 2.040 544 62.
≈ 1.827 469 294.
≈ - 1.555 683 434.
1. 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
3. 在进行实数的运算时,有理数的运算法则及运算性 质同样适用.
2. 实数的大小比较方法有:利用数轴比较、利用绝对 值比较、求平方比较、求差比较、求商比较和计 算近似值比较等方法.
1. 把下列各数填入相应的圈内:
苏科版八年级上册4.3 实数课文ppt课件: 这是一份苏科版八年级上册4.3 实数课文ppt课件,共27页。PPT课件主要包含了无理数的概念,实数的概念,讨论如何分类,有理数,无理数,正无理数,负无理数,正整数,负整数,正分数等内容,欢迎下载使用。
八年级上册4.3 实数课前预习ppt课件: 这是一份八年级上册4.3 实数课前预习ppt课件,共18页。PPT课件主要包含了绝对值性质,下列说法正确的是,不要搞错了,不要遗漏,解下列方程,有理数,无理数,正整数,负整数,正分数等内容,欢迎下载使用。
初中数学4.3 实数课文内容ppt课件: 这是一份初中数学4.3 实数课文内容ppt课件,共18页。PPT课件主要包含了填一填,你知道吗,比较大小,★利用数轴比较大小,做一做,输入时依次按键,第二功能键,方根运算键,小结与回顾,用计算器计算等内容,欢迎下载使用。













