湘教版数学八年级下册 1.1 第2课时 含30°角的直角三角形的性质及其应用 课件

这是一份湘教版数学八年级下册 1.1 第2课时 含30°角的直角三角形的性质及其应用 课件，共26页。

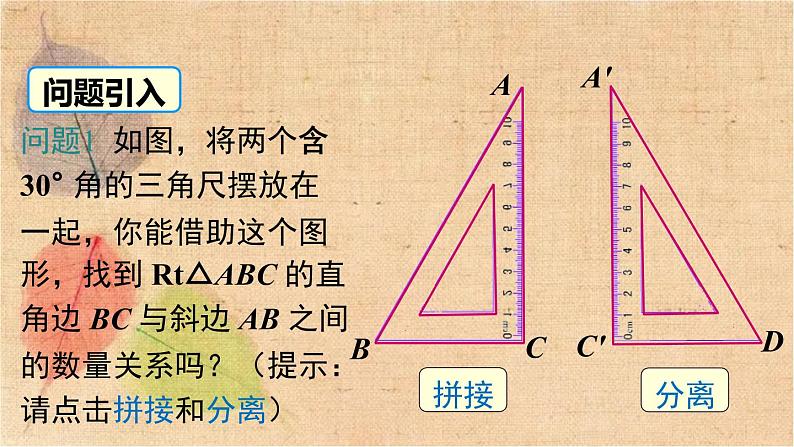
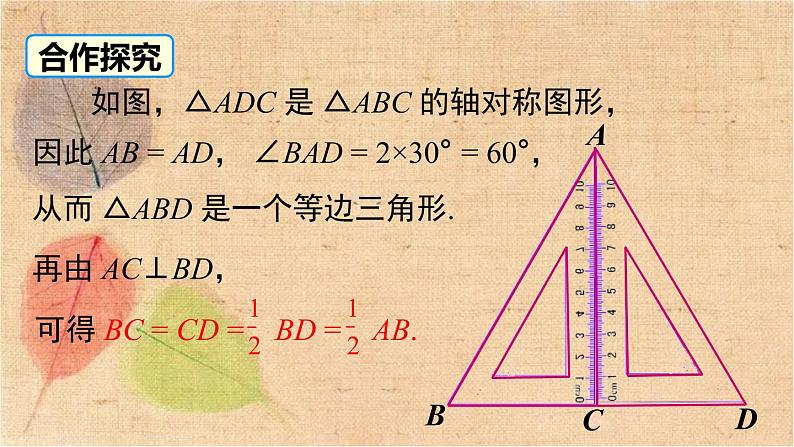
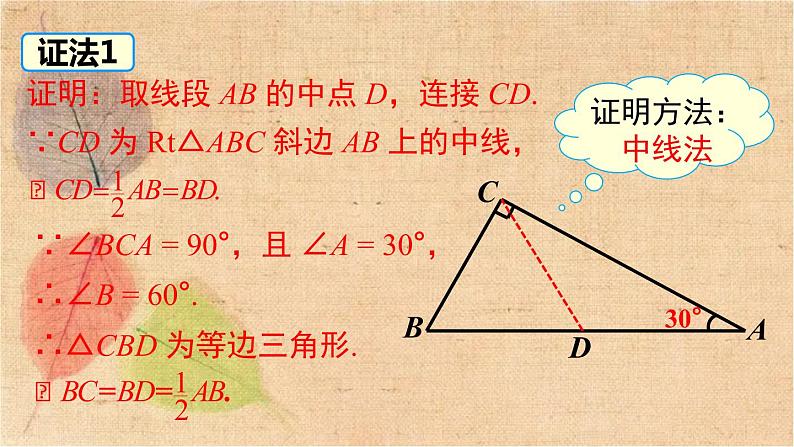
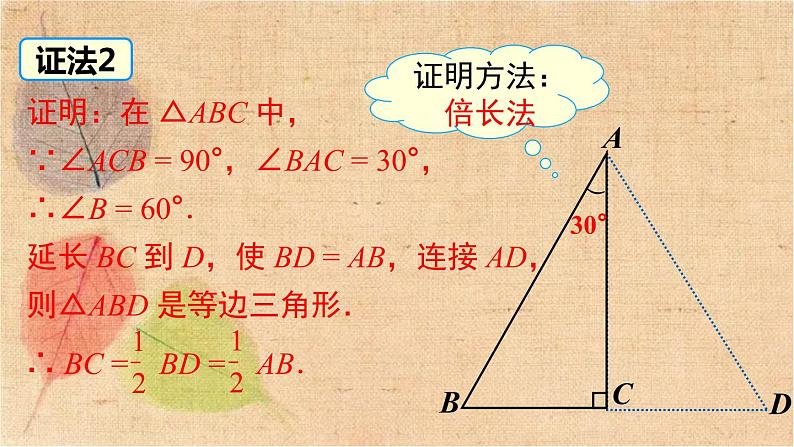
1.1 直角三角形的性质和判定（Ⅰ） 第1章 直角三角形第2课时 含30°角的直角三角形的性质及其应用问题引入问题1 如图，将两个含30° 角的三角尺摆放在一起，你能借助这个图形，找到 Rt△ABC 的直角边 BC 与斜边 AB 之间的数量关系吗？（提示：请点击拼接和分离）分离拼接ABCDA'C'问题2 剪一张等边三角形纸片，沿一边上的高对折，如图所示，你有什么发现？动手：用刻度尺测量含 30°角的直角三角形的斜边和短直角边，比较它们之间的数量关系.含30°角的直角三角形的性质活动探究如图，△ADC 是 △ABC 的轴对称图形，因此 AB = AD， ∠BAD = 2×30° = 60°，从而 △ABD 是一个等边三角形.再由 AC⊥BD，合作探究证明：取线段 AB 的中点 D，连接 CD.∵CD 为 Rt△ABC 斜边 AB 上的中线，∵∠BCA = 90°，且 ∠A = 30°，∴∠B = 60°.∴△CBD 为等边三角形.证法1证法2证明：在 △ABC 中，∵∠ACB = 90°，∠BAC = 30°， ∴∠B = 60°．延长 BC 到 D，使 BD = AB，连接 AD，则△ABD 是等边三角形．30°)) 证明： 在 BA 上截取 BE = BC，连接 EC. ∵ ∠B = 60° ，BE = BC. ∴ △BCE 是等边三角形， ∴ ∠BEC = 60°，BE = EC. ∵ ∠A = 30°， ∴ ∠ECA = ∠BEC -∠A = 60° - 30°= 30°. ∴ AE = EC， ∴ AE = BE = BC， ∴ AB = AE + BE = 2BC.证法330°知识要点含30°角的直角三角形的性质 在直角三角形中，如果一锐角等于30°，那么这个锐角所对的直角边等于斜边的一半.应用格式：∵　在 Rt△ABC 中，∠C = 90°，∠A = 30°，　　)30°(1) 直角三角形中 30° 角所对的直角边等于另一直角边的一半．(2) 三角形中 30° 角所对的边等于最长边的一半.(3) 直角三角形中最小的直角边是斜边的一半.(4) 直角三角形的斜边是 30° 锐角所对直角边的 2 倍．√ 判一判 例1 如图，在 Rt△ABC 中，∠ACB＝90°，∠B＝30°，CD 是斜边 AB 上的高，AD＝3 cm，则 AB 的长度是(　　)A．3 cm B．6 cm C．9 cm D．12 cm典例精析注意：运用含 30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形． D解析：在 Rt△ABC 中，∵CD 是斜边 AB 上的高，∴∠ADC＝90°， ∴∠ACD＝∠B＝30°. 在 Rt△ACD 中，AC＝2AD＝6 cm，在 Rt△ABC 中，AB＝2AC＝12 cm. ∴ AB 的长度是 12 cm.∵∠B = ∠ACB = 15° (已知)，∴∠DAC = ∠B+∠ACB = 15°+15° = 30°，例2 已知：等腰三角形的底角为 15°，腰长为 20. 求腰上的高. ACBD15°15°20解：过 C 作 CD⊥BA 交 BA 的延长线于点 D.))方法总结：在求三角形边长的一些问题中，可以构造含 30° 角的直角三角形来解决．解：∵∠AOD = 30°，AO = 海里，∴ AD = AO= 海里＞20 海里，所以无危险.OBDA北东60°例3 在 A 岛周围 20 海里 (1 海里 = 1852 m) 水域内有暗礁，一轮船由西向东航行到 O 处时，发现 A 岛在北偏东 60° 的方向上，且与轮船相距 海里，如图所示.该船如果保持航向不变，有触暗礁的危险吗？解：如图，取线段 AB 的中点 D，连接 CD.∵CD 是 Rt△ABC 斜边 AB 上的中线，∴CD = AB = BD = BC，即△BDC 为等边三角形．∴∠B = 60°.∵∠B +∠A = 90°，∴∠A = 30°.BCAD知识要点 在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于 30°.应用格式：∵ 在 Rt△ABC 中，∠C = 90°，　)30°∴∠A = 30°例4 如图所示，在四边形 ACBD 中，AD∥BC，AB⊥AC，且 AC ＝ BC，求∠DAC 的度数．解：∵AB⊥AC， ∴∠CAB ＝ 90°.∵AC ＝ BC，∴∠CBA ＝ 30°.∵AD∥BC，∴∠BAD ＝ ∠CBA ＝30°．∴∠DAC ＝ ∠CAB＋∠BAD ＝ 120°.1. 如图，一棵树在一次强台风中，于离地面 3 米处折断倒下，倒下部分与地面成 30° 角，这棵树在折断前的高度为( )A．6 米 B．9 米 C．12 米 D．15 米B2. 某市在旧城改造中，计划在一块如图所示的 △ABC 空地上种植草皮以美化环境，已知∠A ＝ 150°，这种草皮每平方米售价 a 元，则购买这种草皮需要 ( )A．300a 元 B．150a 元C．450a 元 D．225a 元B3. 如图，在 △ABC 中，∠ACB = 90°，CD 是高， ∠A = 30°，AB = 4．则 BD 的长为 . 14. 在 △ABC 中，∠A∶∠B∶∠C = 1∶2∶3，若  AB = 10，则 BC 的长为 .55. 如图，Rt△ABC 中，∠A = 30°，AB + BC = 12 cm，则 AB =______cm.8 第5题图6. 在△ABC 中，∠C = 90°，∠B = 15°，DE 是 AB 的垂直平分线，BE = 5，求 AC 的长．解：连接 AE， ∵DE 是 AB 的垂直平分线，∴BE = AE，∴∠B = ∠EAB = 15°，∴∠AEC = 30°，∵∠C = 90°，7. 在 △ABC 中， AB = AC，∠BAC = 120°，D 是 BC 的中点，DE⊥AB于 E 点，求证：BE = 3AE.证明：∵AB = AC，∠BAC = 120°， ∴∠B = ∠C = 30°.∵ D 是 BC 的中点，∴AD⊥BC.∴∠ADC = 90°，∠BAD = ∠DAC = 60°.∴ AB = 2AD. ∵DE⊥AB，∴∠AED = 90°.∴∠ADE = 30°，∴AD = 2AE.∴ AB = 4AE. ∴BE = 3AE.解：∵DE⊥AC，BC ⊥AC，∠A = 30°，答：立柱 BC 的长是 3.7 m，DE 的长是 1.85 m.8.如图是屋架设计图的一部分，点 D 是斜梁 AB 的中点，立柱 BC，DE 垂直于横梁 AC，AB = 7.4 m，∠A = 30°，立柱 BC、DE 有多长？9. 如图，已知 △ABC 是等边三角形，D，E 分别为BC、AC 上的点，且CD = AE，AD、BE 相交于点 P，BQ⊥AD 于点 Q， 求证：BP = 2PQ.拓展提升∴△ADC≌△BEA.证明：∵△ABC 为等边三角形，∴ AC = BC = AB ，∠C = ∠BAC = 60°.∵CD = AE，∴∠CAD = ∠ABE，∠BAP +∠CAD = 60°.∴∠ABE +∠BAP = 60°.∴∠BPQ = 60°.又∵ BQ⊥AD，∴BP = 2PQ.∴∠PBQ = 30°.∴∠BQP = 90°.内容在直角三角形中，如果一个锐角等于 30°，那么它所对的直角边等于斜边的一半（反之亦成立）使用要点含 30°角的直角三角形的性质找准 30° 的角所对的直角边，点明斜边注意前提条件：含30° 角的直角三角形中