


人教版新课标A选修1-1第二章 圆锥曲线与方程2.1椭圆说课ppt课件
展开2.1 椭圆2.1.1 椭圆及其标准方程
1.了解椭圆的实际背景,经历从具体情境中抽象出椭圆的过程.2.了解椭圆的标准方程的推导及简化过程.3.掌握椭圆的定义、标准方程及几何图形.
在生活中,我们对椭圆并不陌生.油罐汽车的贮油罐横截面的外轮廓线、天体中一些行星和卫星运行的轨道都是椭圆;灯光斜照在圆形桌面上,地面上形成的影子也是椭圆形的.在学习中,椭圆其实比圆更加让我们熟知,无论是数学中的0,还是字母中的O,我们都能看到椭圆的踪影.外表上看起来并不完美的椭圆,因为有了故事,有了情景,反而显得唯美,令人心动.满足什么条件的点的轨迹是椭圆呢?[提示] 到两定点的距离之和等于定值的点的轨迹是椭圆.
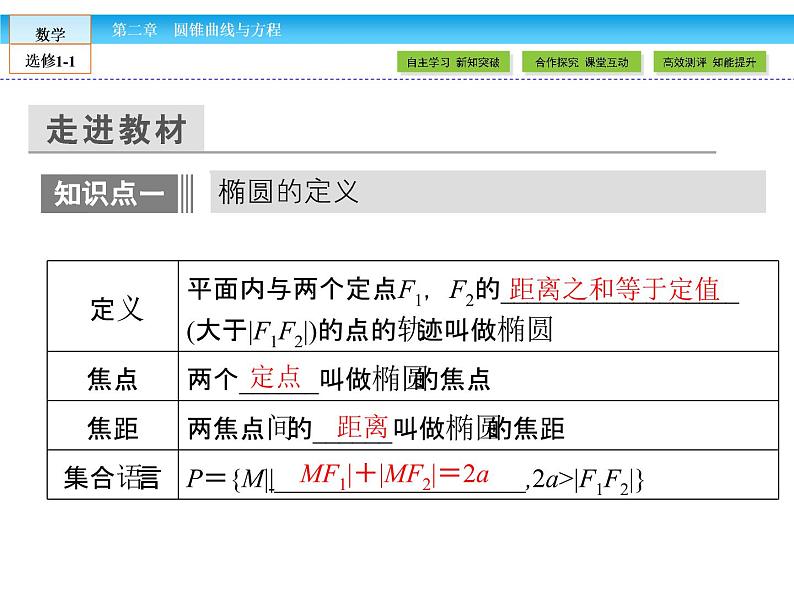
MF1|+|MF2|=2a
对椭圆定义的理解椭圆的定义揭示了椭圆的本质,定义是判断动点轨迹是不是椭圆的重要依据.设集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a,c均为大于0的常数.当2a>2c时,集合P为椭圆;当2a=2c时,集合P为线段F1F2;当2a<2c时,集合P为空集,即动点M的轨迹不存在.
对椭圆标准方程的三点认识(1)标准的几何特征:椭圆的中心在坐标原点,焦点在x轴或y轴上,对称轴是坐标轴.(2)标准的代数特征:方程右边是1,左边是关于x,y的平方和,并且分母不相等.
(3)a,b,c三个量的关系:椭圆的标准方程中,a表示椭圆上的点M到两焦点间距离的和的一半,可借助图形帮助记忆.a,b,c(都是正数)恰是构成一个直角三角形的三条边,a是斜边,所以a>b,a>c,且a2=b2+c2.
答案: (-6,-2)∪(3,+∞)
下列说法中正确的是( )A.已知F1(-4,0),F2(4,0),到F1,F2两点的距离之和等于8的点的轨迹是椭圆B.已知F1(-4,0),F2(4,0),到F1,F2两点的距离之和为6的点的轨迹是椭圆C.到F1(-4,0),F2(4,0)两点的距离之和等于点M(5,3)到F1,F2的距离之和的点的轨迹是椭圆D.到F1(-4,0),F2(4,0)距离相等的点的轨迹是椭圆
[思路点拨] 椭圆是到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹,应特别注意椭圆的定义的应用.
并不是动点到两定点距离之和为常数的点的轨迹就一定是椭圆,只有当距离之和大于两定点之间的距离时得到的轨迹才是椭圆.
1.命题甲:动点P到两定点A,B的距离之和|PA|+|PB|=2a(a>0且a为常数);命题乙:点P的轨迹是椭圆,且A,B是椭圆的焦点.则命题甲是命题乙的( )A.充分不必要条件 B.必要不充分条件C.充分且必要条件D.既不充分又不必要条件解析: 当2a>|F1F2|时是椭圆,当2a=|F1F2|时是线段,当2a<|F1F2|时无轨迹,所以选B.答案: B
(1)求椭圆标准方程的一般步骤为:
椭圆的定义与标准方程的综合应用
在解答解析几何的习题时,要善于根据曲线和图形的性质,用平面几何的知识加以解答,本题综合运用了余弦定理和椭圆的定义,从而简化了运算,达到化繁为简的目的.
3.已知F1,F2是椭圆9x2+25y2=225的左,右焦点.点P是椭圆上一点,且其横坐标为2,求|PF1|与|PF2|.
2021学年2.2直接证明与间接证明多媒体教学课件ppt: 这是一份2021学年2.2直接证明与间接证明多媒体教学课件ppt,共32页。PPT课件主要包含了x≥0,x≤0,y≥0,y≤0,e=1,x1+x2+p,k2x2+,平行或重合,解得k=±2,=x1+x2+p等内容,欢迎下载使用。
数学选修1-22.1合情推理与演绎推理课堂教学课件ppt: 这是一份数学选修1-22.1合情推理与演绎推理课堂教学课件ppt,共33页。PPT课件主要包含了-a≤x≤a,-b≤y≤b,-b≤x≤b,-a≤y≤a,接近1,接近0,则a=5b=1,椭圆离心率的求法等内容,欢迎下载使用。
高中数学人教版新课标A选修1-22.1合情推理与演绎推理背景图课件ppt: 这是一份高中数学人教版新课标A选修1-22.1合情推理与演绎推理背景图课件ppt,共32页。PPT课件主要包含了差的绝对值,双曲线,a0b0,-c0,0-c,a2+b2,数形结合思想的应用等内容,欢迎下载使用。