人教版新课标A选修1-12.1椭圆教学课件ppt

这是一份人教版新课标A选修1-12.1椭圆教学课件ppt，共19页。PPT课件主要包含了画椭圆，完善定义，求椭圆的方程，代入坐标，焦点在y轴，焦点在x轴，F±c0，F0±c，abc之间的关系，由椭圆的定义知等内容，欢迎下载使用。

生活中有椭圆，生活中用椭圆
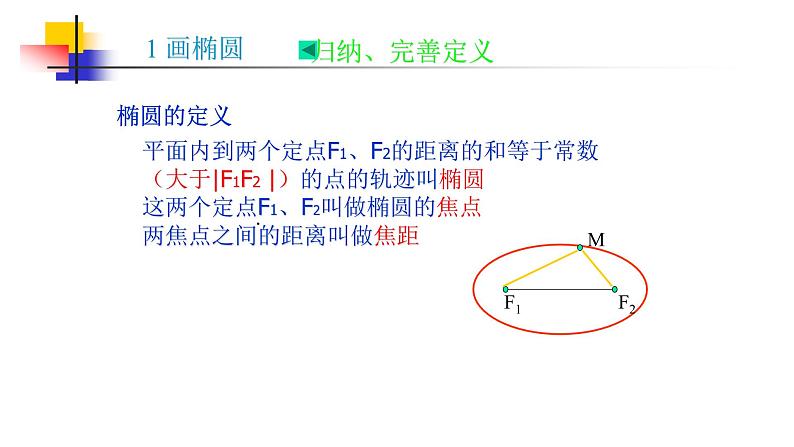
平面内到两个定点F1、F2的距离的和等于常数（大于|F1F2 |）的点的轨迹叫椭圆这两个定点F1、F2叫做椭圆的焦点两焦点之间的距离叫做焦距
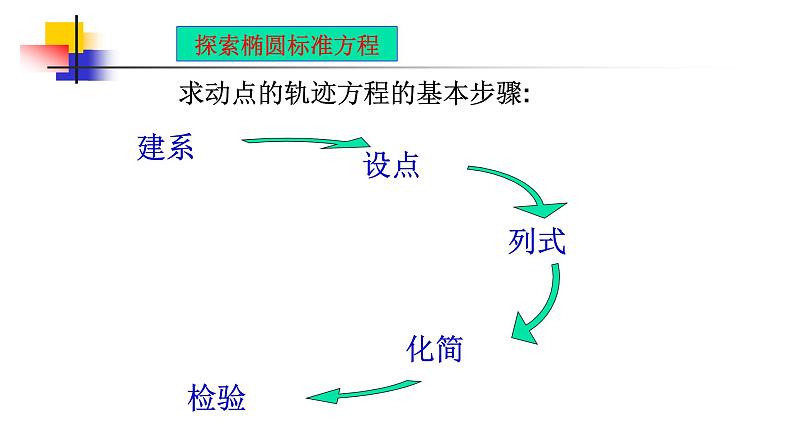
求动点的轨迹方程的基本步骤:
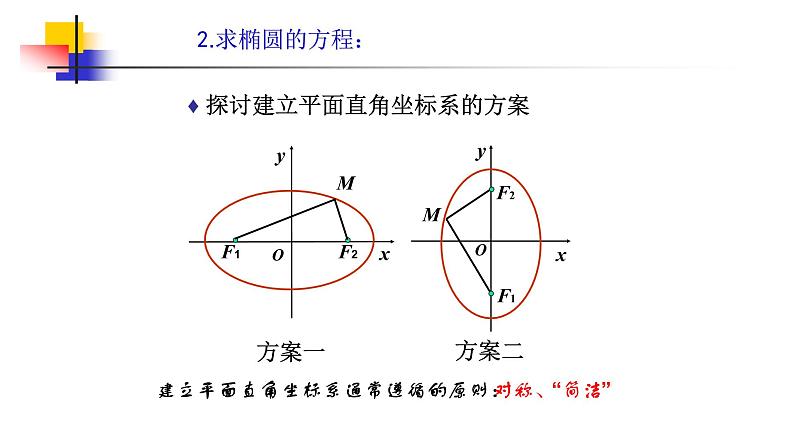
♦ 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则：对称、“简洁”
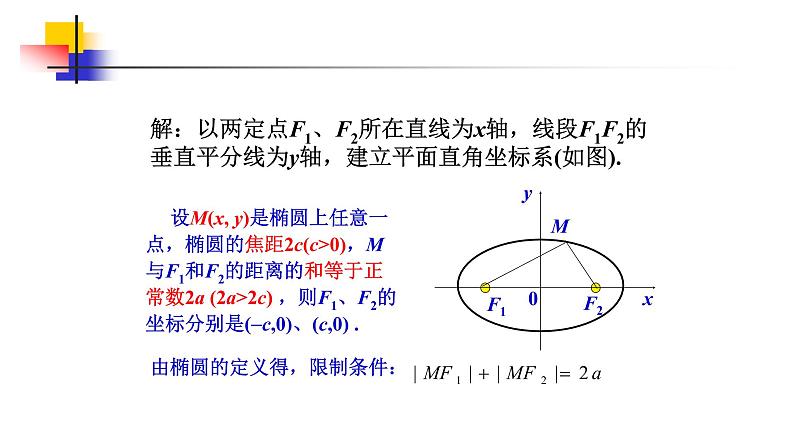
解：以两定点F1、F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点，椭圆的焦距2c(c>0)，M与F1和F2的距离的和等于正常数2a (2a>2c) ，则F1、F2的坐标分别是(c,0)、(c,0) .
由椭圆的定义得，限制条件：
（问题：下面怎样化简？）
总体印象：对称、简洁，“像”直线方程的截距式
|MF1|+|MF2|=2a (2a>2c>0)
共同点：椭圆的标准方程表示的一定是焦点在坐标轴上，中心在坐标原点的椭圆；方程的左边是平方和，右边是1.
例1、写出适合下列条件的椭圆的标准方程
两个焦点的坐标是（ 0 ，-2）和（ 0 ，2），并且经 过点P
解： 因为椭圆的焦点在y轴上， 设它的标准方程为
∵ c=2，且 c2= a2 - b2
∴ 4= a2 - b2 ……①
(法二) 因为椭圆的焦点在y轴上，所以设它的 标准方程为
所以所求椭圆的标准方程为
练习1.下列方程哪些表示椭圆？
若是,则判定其焦点在何轴？
练习2. 已知椭圆的方程为： ，请填空：(1) a=__，b=__，c=__，焦点坐标为___________，焦距等于__.(2)若C为椭圆上一点，F1、F2分别为椭圆的左、右焦点， 并且CF1=2,则CF2=___.
(-3,0)、(3,0)
练习3 、已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆，它的焦距为2.4m，外轮廓线上的点到两个焦点距离的和为3m，求这个椭圆的标准方程．
小结：1、椭圆的标准方程是什么？
①定位：确定焦点所在的坐标轴； ②定量：求a, b的值.
2、求椭圆标准方程的步骤是什么？
布置作业：教科书习题2.3 A组第1、2题。