人教版数学八下同步讲练课件18.2 特殊的平行四边形 第五课时

这是一份人教版数学八下同步讲练课件18.2 特殊的平行四边形 第五课时，共48页。
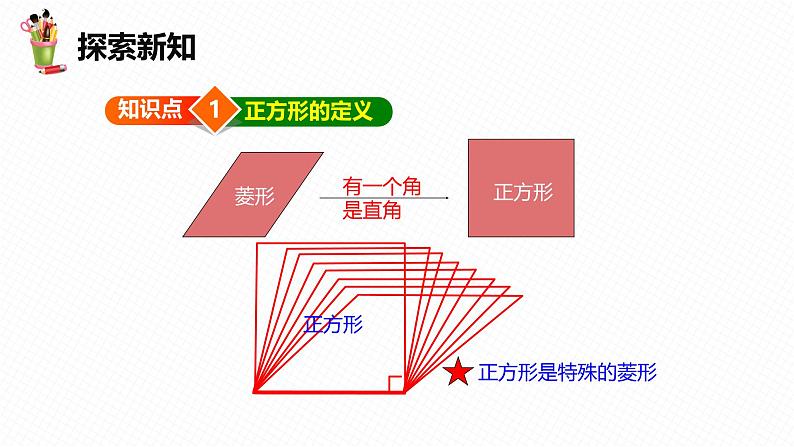
18.2 特殊的平行四边形第5课时目录课前导入新课精讲学以致用课堂小结课前导入情景导入回顾旧知识：平行四边形边：角：对角线：对边平行且相等对角相等，邻角互补对角线互相平分矩形角：四个角是直角对角线：对角线相等且互相平分边：对边平行且相等具有平行四边形所有性质情景导入菱形的性质边：四条边相等对角线：互相垂直平分分别平分两组对角对角相等,邻角互补具有平行四边形一切性质角：回顾旧知识：新课精讲探索新知1知识点正方形的定义正方形正方形有一个角是直角探索新知正方形的概念：__________________________________ 的平行四边形是正方形._______________的菱形是正方形._________________的矩形是正方形. 定义有一组邻边相等且有一个角是直角的有一个角是直角有一组邻边相等探索新知例1 如图，已知点E 是正方形ABCD 的边CD 上一点，点 F 是CB 的延长线上一点，且EA⊥AF. 求证：DE =BE.本题要证明两条线段相等，而证明线段相等的方法有很多，根据题中所给的条件，由正方形ABCD，我们可以得到边相等，角相等，也可以得到平行，所以在可以得到比较多的条件的情况下，一般会想到用全等去解决，而本题中全等的条件也很充足，那么问题即可解决．分析：探索新知∵四边形ABCD 是正方形，∴AD =AB，∠D =∠ABF=∠BAD=90°．∴∠BAE+∠EAD =90°．∴EA⊥AF， ∴∠BAE +∠FAB =90°．∴∠EAD =∠FAB．∴△ABF ≌ △ADE．∴DE=BF.证明：探索新知知道正方形就说明它的四边都相等，四个角都是直角.典题精讲下面四个定义中不正确的是(　　)A．有一个角是直角的平行四边形叫做矩形B．有一组邻边相等的四边形叫做菱形C．有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形D．有一组邻边相等的平行四边形叫做菱形1B▱ABCD 的对角线AC 与BD 相交于点O，且AC⊥BD，请添加一个条件：_____________，使得▱ABCD 为正方形．2AC＝BD探索新知2知识点正方形边的性质正方形边的性质： 具有矩形、菱形、平行四边形的一切性质，即四条边相等，邻边垂直，对边平行；探索新知例2 已知：如图，在正方形ABCD 中，对角线的交 点为O，E 是OB上的一点，DG⊥AE 于G，DG 交AO 于F，求证：EF∥AB.要证EF∥AB，由于∠OBA＝45°，∠EOF＝90°，即需证∠OEF＝45°，即要证明OE＝OF，而OE＝OF 可通过证明△AEO ≌ △DFO 获得．导引：探索新知∵四边形ABCD 是正方形，∴∠AOE＝∠DOF＝90°，AO＝DO，∠OBA＝45°.又∵DG⊥AE，∴∠EAO＋∠AEO＝∠EDG＋∠GED＝90°.∵∠AEO＝∠GED，∴∠EAO＝∠EDG＝∠FDO.∴△AEO ≌ △DFO (ASA)．∴OE＝OF.∴∠OEF＝45°. ∴∠OEF＝∠OBA.∴EF∥AB.证明：探索新知 通过证明三角形全等得到边和角相等，再进一步得到平行或垂直，是有关正方形中证边或角相等的最常用的方法，而正方形的四条边相等，四个角都是直角为证明三角形全等提供了条件．典题精讲(1)把一张长方形纸片按如图方式折一下，就可以裁出正方形纸片. 为什么？ (2)如何从一块长方形木板中裁出一块最大的正方形木板呢？1略.解：典题精讲正方形具有而矩形不一定具有的性质是(　　)A．四个角都相等 B．四条边相等C．对角线相等 D．对角线互相平分2B典题精讲一个大矩形按如图方式分割成九个小矩形，且只有标号为①和②的两个小矩形为正方形，在满足条件的所有分割中，若知道九个小矩形中n 个小矩形的周长，就一定能算出这个大矩形的面积，则n 的最小值是(　　)A．3 B．4 C．5 D．63A典题精讲如图，正方形ABCD 的面积为1，则以相邻两边中点连线EF 为边的正方形EFGH 的周长为(　　)　A. B．2C. ＋1 D．2 ＋14B探索新知3知识点正方形角的性质正方形角的性质：四个角相等，且都是直角。探索新知例3 如图，正方形ABCD 的边长为1 cm，AC 为对角线， AE 平分∠BAC，EF⊥AC，求BE 的长．线段BE 是Rt△ABE 的一边，但由于AE 未知，不能直接用勾股定理求BE，由条件可证△ABE ≌ △AFE，问题转化为求EF 的长，结合已知条件易获解．导引：探索新知 ∵四边形ABCD 为正方形， ∴∠B＝90°，∠ACB＝45°，AB＝BC＝1 cm. ∵EF⊥AC，∴∠EFA＝∠EFC＝90°. 又∵∠ECF＝45°， ∴△EFC 是等腰直角三角形，∴EF＝FC. ∵∠BAE＝∠FAE，∠B＝∠EFA＝90°，AE＝AE， ∴△ABE ≌ △AFE. ∴AB＝AF＝1 cm，BE＝EF，∴FC＝BE. 在Rt△ABC 中，AC ∴FC＝AC－AF＝( －1)(cm)，∴BE＝( －1) cm.解：探索新知 解有关正方形的问题，要充分利用正方形的四边相等、四角相等、对角线垂直平分且相等等性质，正方形的性质、等腰直角三角形的特点、勾股定理是解决正方形的相关证明与计算问题的三把钥匙．典题精讲如图，ABCD 是一块正方形场地. 小华和小芳在AB 边上取定了一点E，测量知， EC=30 m，EB = 10 m. 这块场地的面积和对角线长分别是多少？1典题精讲连接AC，BD 相交于点O.在Rt△BCE 中，BC因为AB＝BC＝CD＝AD，所以S正方形ABCD＝BC 2＝(20)2＝800(m2)．因为AC又BD＝AC，所以BD＝40 m．所以这块场地的面积是800 m2，对角线长是40 m.解：典题精讲如图是边长为10 cm的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据(单位：cm)不正确的是(　　)2A典题精讲如图，在正方形ABCD 中，△ABE 和△CDF 为直角三角形，∠AEB＝∠CFD＝90°，AE＝CF＝5，BE＝DF＝12，则EF 的长是(　　)A．7 B．8 C．7 D．73C易错提醒如图，正方形ABCD 的边长为4，E 为BC 上的一点，BE＝1，F 为AB 上的一点，AF＝2，P 为AC 上一个动点，则PF＋PE 的最小值为________．易错点：不能将两线段和转化为一条线段而致错.易错提醒学以致用小试牛刀如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH. 若BE∶EC＝2∶1，则线段CH 的长是(　　)A．3　　　 B．4　　　 C．5　　　 D．61B小试牛刀已知在四边形ABCD 中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是(　　)A．∠D＝90° B．AB＝CDC．AD＝BC D．BC＝CD2D小试牛刀我们知道：四边形具有不稳定性.如图，在平面直角坐标系中，边长为2的正方形ABCD 的边AB 在x 轴上，AB 的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D 落在y轴正半轴上点D ′处，则点C 的对应点C ′的坐标为(　　)A．( ，1) B．(2，1)C．(1， ) D．(2， )3D小试牛刀4 如图，四边形ABCD 是正方形，△EBC 是等边三角形． (1)求证：△ABE ≌ △DCE； (2)求∠AED 的度数．小试牛刀(1)∵四边形ABCD 是正方形， ∴AB＝BC＝CD，∠ABC＝∠DCB＝90°. ∵△EBC 是等边三角形， ∴EB＝BC＝EC， ∠EBC＝∠ECB＝∠BEC＝60°. ∴∠EBA＝∠ECD＝30°. 在△ABE 和△DCE 中， ∴△ABE ≌ △DCE.证明：小试牛刀(2)由(1)可知，AB＝BE，∠ABE＝30°. ∴∠BAE＝∠BEA＝75°. 同理∠CDE＝∠CED＝75°. ∴∠AED＝360°－75°－75°－60°＝150°.小试牛刀如图，在正方形ABCD 中，E，F 分别为边AD 和CD 上的点，且AE＝CF，连接AF，CE 交于点G.求证：AG＝CG.小试牛刀∵四边形ABCD 是正方形，∴∠ADF＝90°，AD＝CD.∵AE＝CF，∴DE＝DF.在△ADF 和△CDE 中，∴△ADF ≌ △CDE (SAS)，∴∠DAF＝∠DCE.在△AGE 和△CGF 中，∴△AGE ≌ △CGF (AAS)，∴AG＝CG.证明：小试牛刀如图，正方形ABCD 中，G 为BC 边上一点，BE⊥AG 于E， DF⊥AG 于F，连接DE. (1)求证：△ABE ≌ △DAF； (2)若AF＝1，四边形ABED 的面积为6，求EF 的长．小试牛刀(1)在正方形ABCD 中，AB＝AD，∠BAD＝90°， ∴∠BAE＋∠DAF＝90°. ∵BE⊥AG 于E，DF⊥AG 于F， ∴∠AEB＝∠DFA＝90°， ∠ADF＋∠DAF＝90°， ∴∠BAE＝∠ADF， ∴△ABE ≌ △DAF (AAS)．证明：小试牛刀(2)∵△ABE ≌ △DAF， ∴BE＝AF＝1，AE＝DF， 设AE＝DF＝x，∵S四边形ABED＝S△ABE＋S△ADE， ∴6＝ AE (BE＋DF )， ∴6＝ x (1＋x )，整理得x 2＋x－12＝0， ∴(x－3)(x＋4)＝0. ∴x1＝3，x2＝－4(舍去)， ∴AE＝3， ∴EF＝AE－AF＝2.解：小试牛刀如图，在正方形ABCD 中，点G 在对角线BD 上(不与点B， D 重合)，GE⊥DC 于点E，GF⊥BC 于点F，连接AG. (1)写出线段AG，GE，GF 长度之间的等量关系，并说明理由； (2)若正方形ABCD 的边长为1，∠AGF＝105°，求线段BG 的长．小试牛刀(1)AG 2＝GE 2＋GF 2. 理由如下：如图，连接GC，由正方形的性质知AD＝CD，∠ADG＝∠CDG.在△ADG 和△CDG 中，所以△ADG ≌ △CDG，所以AG＝CG.由题意知∠GEC＝∠GFC＝∠DCB＝90°，所以四边形GFCE 为矩形，CG 2＝CF 2＋GF 2，所以GE＝FC.又因为AG＝CG，所以AG 2＝GE 2＋GF 2.解：小试牛刀(2)如图，作AH⊥BD于点H， 由题意易知∠AGB＝60°，∠ABG＝45°， 所以∠BAH＝45°＝∠ABG，∠GAH＝30°， 所以AH＝BH，AG＝2HG. 因为AB＝1， 所以在Rt△ABH 中，由勾股定理可得AH＝BH＝ . 在Rt△AGH 中，由勾股定理可得HG＝ . 所以BG＝ .课堂小结课堂小结1.正方形是中心对称图形，轴对称图形.2.正方形的四条边都相等.3.正方形的四个角都相等.4.正方形的对角线互相垂直平分且相等，且每一条对角线平分一组对角.同学们，下节课见！