人教版数学八下同步讲练课件18.2 特殊的平行四边形 第六课时

这是一份人教版数学八下同步讲练课件18.2 特殊的平行四边形 第六课时，共43页。
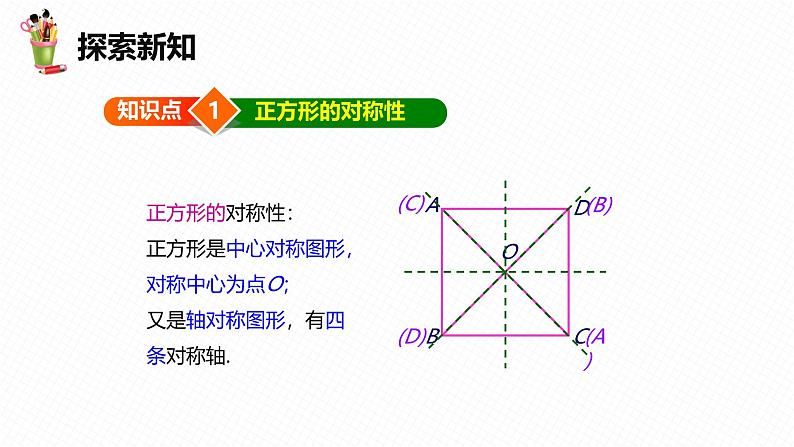
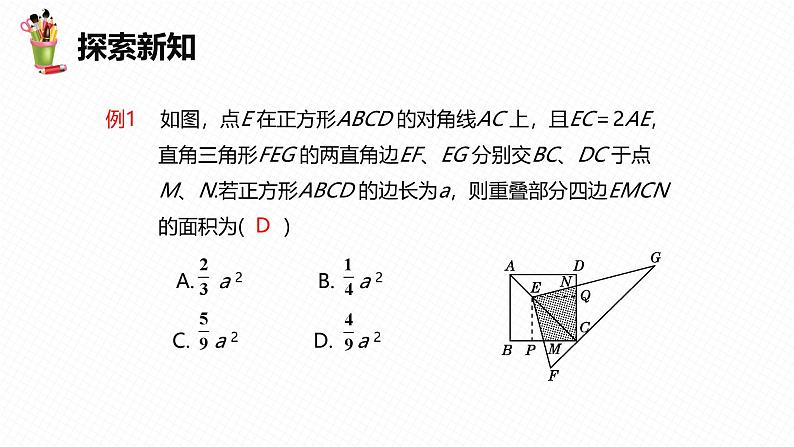
18.2 特殊的平行四边形第6课时目录课前导入新课精讲学以致用课堂小结课前导入情景导入回顾旧知识：①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形 ①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形菱形的判别方法：矩形的判别方法：新课精讲探索新知1知识点正方形的对称性(A)(B)(C)(D)正方形的对称性：正方形是中心对称图形，对称中心为点O；又是轴对称图形，有四条对称轴.探索新知例1 如图，点E 在正方形ABCD 的对角线AC 上，且EC＝2AE， 直角三角形FEG 的两直角边EF、EG 分别交BC、DC 于点 M、N.若正方形ABCD 的边长为a，则重叠部分四边EMCN 的面积为(　　) A. a 2　　 B. a 2　 　 C. a 2　 　D. a 2D探索新知作EP⊥BC 于点P，EQ⊥CD 于点Q，易得△EPM ≌ △EQN，利用四边形EMCN 的面积等于正方形PCQE 的面积求解．作EP⊥BC 于点P，EQ⊥CD 于点Q，∵四边形ABCD 是正方形，∴∠BCD＝90°，又∵∠EPM＝∠EQN＝90°，∴∠PEQ＝90°，∴∠PEM＋∠MEQ＝90°，∵三角形FEG 是直角三角形，∴∠NEF＝∠NEQ＋∠MEQ＝90°，∴∠PEM＝∠NEQ，∵CA是∠BCD 的角平分线，∠EPC＝∠EQC＝90°，∴EP＝EQ，四边形PCQE 是正方形，导引：探索新知在△EPM 和△EQN 中，∴△EPM ≌ △EQN (ASA)，∴S△EQN＝S△EPM，∴四边形EMCN 的面积等于正方形PCQE 的面积，∵正方形ABCD 的边长为a，∴AC＝ a，∵EC＝2AE，∴EC＝ a，∴EP＝PC＝ a，∴正方形PCQE 的面积＝ a× a＝ a 2，∴四边形EMCN 的面积＝ a 2.探索新知 本例解法在于巧用割补法，将分散的图形拼合在一起，将不规则的阴影面积集中到一个规则的图形中，再利用正方形及三角形的性质求出，解答过程体现了割补法及转化思想．典题精讲1如图，菱形ABCD 的面积为120 cm2，正方形AECF 的面积为50 cm2，则菱形的边长为________．13cm2小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了(　　)A．1次　 B．2次C．3次 D．4次B典题精讲3将五个边长都为2 cm的正方形按如图所示方式摆放，点A，B，C，D 分别是四个正方形的中心，则图中四块阴影部分面积的和为(　　)A．2 cm2 B．4 cm2C．6 cm2 D．8 cm2B探索新知2知识点正方形的判定正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形.正方形的性质=探索新知有一组邻边相等有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等探索新知例2 如图，在△ABC 中，∠ACB＝90°，CD 平分∠ACB， DE⊥BC，DF⊥AC，垂足分别为E，F. 求证：四边 形CFDE 是正方形．要证四边形CFDE 是正方形，首先要确定这个正方形建立在哪种四边形的基础上，即先证它是什么四边形；再证这种四边形是正方形需要补充的条件．导引：探索新知证法一：∵DE⊥BC，AC⊥BC，∴DE∥CF. 同理DF∥CE， ∴四边形CFDE 是平行四边形． ∵CD 平分∠ACB，DE⊥BC，DF⊥AC， ∴DE＝DF，∴▱ CFDE 是菱形． ∵∠ACB＝90°，∴菱形CFDE 是正方形．证法二：∵∠ECF＝∠CFD＝∠CED＝90°， ∴四边形CFDE 是矩形． ∵CD 平分∠ACB，DE⊥BC，DF⊥AC， ∴DE＝DF，∴矩形CFDE 是正方形．探索新知证明条件中不含对角线的四边形是正方形的四种方法：方法1：证：“四边形＋四边相等＋四个直角”；方法2：证：“平行四边形＋一组邻边相等＋一个直角”；方法3：证：“矩形＋一组邻边相等”；方法4：证：“菱形＋一个直角”．探索新知例3 如图，已知在▱ABCD 中，对角线AC，BD 交于点O，E 是BD 的延长线上的点，且EA＝EC. (1)求证：四边形ABCD是菱形； (2)若∠DAC＝∠EAD＋∠AED， 求证：四边形ABCD 是正方形．要证▱ABCD是正方形，有三种途径可走：即在平行四边形、菱形、矩形的基础上，找各需补充的对角线的条件进行证明；若要证明▱ABCD是菱形，由于题中条件与对角线相关，则需证AC⊥BD.导引：探索新知(1)首先根据平行四边形的性质可得AO＝CO，再由EA＝EC 可得△EAC 是等腰三角形，然后根据等腰三角形三线合一的性质可得EO⊥AC，根据对角线互相垂直的平行四边形是菱形可证出结论；(2)首先根据角的关系得出AO＝DO，进而得到AC＝BD，再根据对角线相等的菱形是正方形可得到结论．探索新知 (1)∵四边形ABCD 是平行四边形，∴AO＝CO， ∵EA＝EC，∴EO⊥AC，即BD⊥AC， ∴四边形ABCD 是菱形． (2)∵∠ADO＝∠EAD＋∠AED， ∠DAC＝∠EAD＋∠AED， ∴∠ADO＝∠DAC，∴AO＝DO， ∵四边形ABCD 是菱形， ∴AC＝2AO，BD＝2DO， ∴AC＝BD，∴四边形ABCD 是正方形.证明：探索新知证明条件中含对角线的四边形是正方形的方法：(1)证：“四边形＋对角线互相垂直、平分且相等”；(2)证：“平行四边形＋对角线互相垂直且相等”；(3)证：“矩形＋对角线互相垂直”；(4)证：“菱形＋对角线相等”．典题精讲1 满足下列条件的四边形是不是正方形？为什么？(1) 对角线互相垂直且相等的平行四边形；(2) 对角线互相垂直的矩形；(3) 对角线相等的菱形；(4) 对角线互相垂直平分且相等的四边形.(1)是；(2)是；(3)是；(4)是．原因略．解：典题精讲2如图，在菱形ABCD 中，对角线AC，BD 相交于点O，不添加任何辅助线，请添加一个条件___________________________，使四边形ABCD 是正方形．∠BAD＝90°(答案不唯一)典题精讲3下列判断错误的是(　　)A．两组对边分别相等的四边形是平行四边形B．四个内角都相等的四边形是矩形C．四条边都相等的四边形是菱形D．两条对角线垂直且互相平分的四边形是正方形D易错提醒四边形ABCD 的对角线AC 和BD 相交于点O，假设有下列条件：①AB＝AD ； ②∠DAB＝90°；③AO＝CO，BO＝DO； ④四边形ABCD 为矩形；⑤四边形ABCD 为菱形； ⑥四边形ABCD 为正方形．则下列推理不成立的是(　　)A．①④⇒⑥ B．①③⇒⑤C．①②⇒⑥ D．②③⇒④易错点：将特殊四边形的判定相混淆导致出错.C学以致用小试牛刀1关于▱ABCD 的叙述，正确的是(　　)A．若AB⊥BC，则▱ABCD是菱形B．若AC⊥BD，则▱ABCD是正方形C．若AC＝BD，则▱ABCD是矩形D．若AB＝AD，则▱ABCD是正方形C小试牛刀2小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD中选两个作为补充条件，使▱ABCD 为正方形(如图)，现有下列四种选法，你认为其中错误的是(　　) A．①②B．②③C．①③D．②④B小试牛刀3在△ABC 中，点D，E，F 分别在BC，AB，CA上，且DE∥CA，DF∥BA，连接EF，AD，则下列三种说法：①如果EF＝AD，那么四边形AEDF 是矩形；②如果EF⊥AD，那么四边形AEDF 是菱形；③如果AD⊥BC 且AB＝AC，那么四边形AEDF 是正方形，其中正确的有(　　)A．3个 B．2个 C．1个 D．0个B小试牛刀已知：如图，在菱形ABCD 中，点E，O，F 分别为AB， AC，AD 的中点，连接CE，CF，OE，OF. (1)求证：△BCE ≌ △DCF. (2)当AB 与BC 满足什么关系时，四边形AEOF 是正方形？ 请说明理由．小试牛刀(1)∵四边形ABCD 是菱形， ∴AB＝BC＝CD＝DA，∠B＝∠D. ∵点E，F 分别为AB，AD 的中点， ∴BE＝ AB，DF＝ AD. ∴BE＝DF. 在△BCE 和△DCF 中， ∴△BCE ≌ △DCF (SAS)．证明：小试牛刀(2)AB⊥BC，理由如下： ∵点E，O，F 分别为AB，AC，AD 的中点， ∴OE＝ BC＝ AD＝AF. 同理可证：OF＝AE＝ AB； ∴OE＝OF＝AF＝AE. ∴四边形AEOF 是菱形． ∵AB⊥BC，又易知OE∥BC，∴AE⊥OE. ∴四边形AEOF 是正方形．解：小试牛刀如图，已知在△ABC 中，AB＝AC，D 为BC 边的中点， 过点D 作DE⊥AB，DF⊥AC，垂足分别为E，F. (1)求证：△BED ≌ △CFD； (2)若∠A＝90°，求证：四边形DFAE 是正方形．小试牛刀(1)∵DE⊥AB，DF⊥AC， ∴∠BED＝∠CFD＝90°. ∵AB＝AC，∴∠B＝∠C. ∵D 是BC 的中点，∴BD＝CD. ∴△BED ≌ △CFD.(2)∵DE⊥AB，DF⊥AC， ∴∠AED＝∠AFD＝90°. ∵∠A＝90°，∴四边形DFAE 为矩形． ∵△BED ≌ △CFD，∴DE＝DF. ∴四边形DFAE 是正方形．证明：小试牛刀如图，在△ABC 中，∠BAC＝90°，AD 是中线，E 是AD 的中点，过点A作AF∥BC 交BE 的延长线于点F，连接CF. (1)求证：AD＝AF； (2)如果AB＝AC，试判断四边形ADCF 的形状，并证明你的结论．小试牛刀(1)∵AF∥BC，∴∠EAF＝∠EDB. ∵E 是AD 的中点，∴AE＝DE. 又∵∠AEF＝∠DEB， ∴△AEF ≌ △DEB (ASA)． ∴AF＝DB. ∵在△ABC 中，∠BAC＝90°，AD 是中线， ∴AD＝BD＝DC＝ BC. ∴AD＝AF.证明：小试牛刀(2)当AB＝AC 时，四边形ADCF 是正方形． 由(1)可知，AD＝AF＝DC， ∵AF∥BC， ∴四边形ADCF 是平行四边形． ∵AB＝AC，AD 是中线，∴AD⊥BC. 又∵AD＝AF，∴四边形ADCF 是正方形．解：小试牛刀如图，在等腰三角形ABC 中，∠ACB＝90°，AC＝BC＝4， D 是AB 的中点，E，F 分别是AC，BC 上的点(点E 不与端 点A，C 重合)，且AE＝CF，连接EF 并取EF 的中点O，连 接DO 并延长至点G，使GO＝DO，连接DE，DF，GE，GF. (1)求证：四边形EDFG 是正方形； (2)当点E 在什么位置时，四边形EDFG 的面积最小？并求四 边形EDFG 面积的最小值．小试牛刀(1)如图，连接CD. ∵O是EF 的中点，∴OE＝OF. 又∵OD＝OG，∴四边形EDFG 为平行四边形． ∵AC＝BC，D 为AB 的中点，∠ACB＝90°， ∴AD＝DC，∠A＝∠FCD＝45°，CD⊥AB. 在△AED 和 △CFD 中，AE＝CF，∠A＝∠FCD， AD＝DC，∴△AED ≌ △CFD. ∴DE＝DF，∠ADE＝∠CDF. ∴四边形EDFG 为菱形． ∵CD⊥AD，∴∠ADE＋∠EDC＝90°. ∴∠EDC＋∠CDF＝90°，即∠EDF＝90°. ∴四边形EDFG 为正方形．证明：小试牛刀(2)∵四边形EDFG 为正方形， ∴当正方形EDFG 的边长DE 最短时，其面积最小． ∵垂线段最短， ∴当DE⊥AC 时，四边形EDFG 的面积最小． ∵AD＝DC，DE⊥AC， ∴AE＝EC，DE＝ AC＝2. ∴当E 为AC 的中点时，四边形EDFG 的面积最小， 四边形EDFG 的面积的最小值＝22＝4.解：课堂小结课堂小结5种识别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等四边形平行四边形矩形菱形正方形同学们，下节课见！