数学八年级上册2.2 轴对称的性质完美版ppt课件

这是一份数学八年级上册2.2 轴对称的性质完美版ppt课件，共18页。PPT课件主要包含了情境导入，轴对称的性质，活动一，活动二，ABA′B′，活动三，说一说，回顾与思考等内容，欢迎下载使用。

如果两个图形成轴对称，那么这两个图形的形状与大小有怎样的关系？
成轴对称的两个图形全等
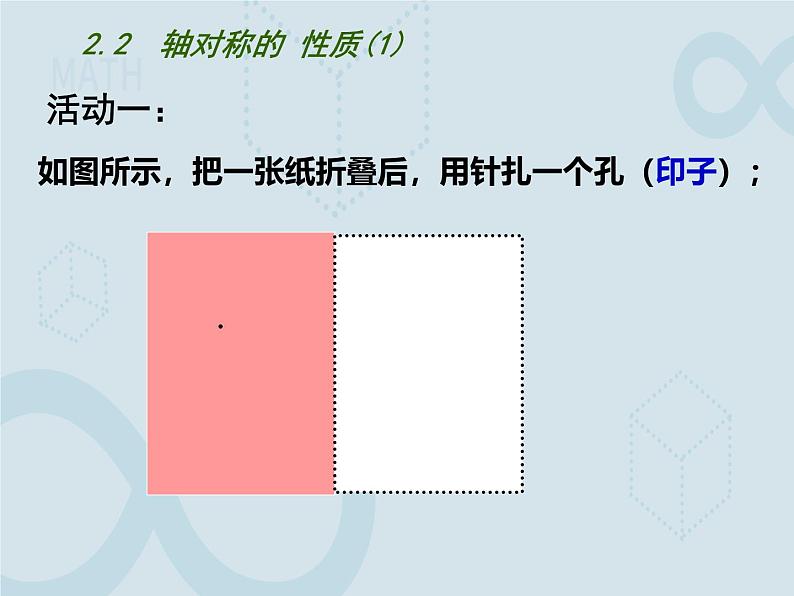
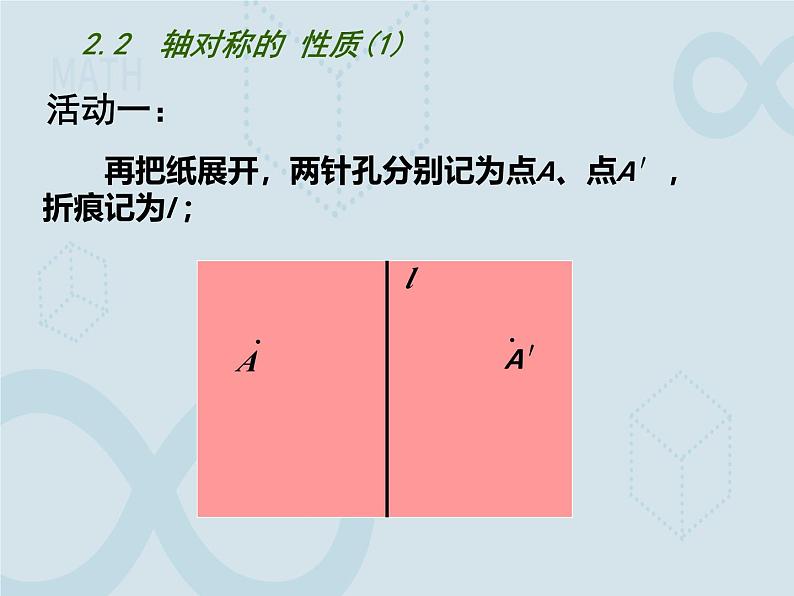
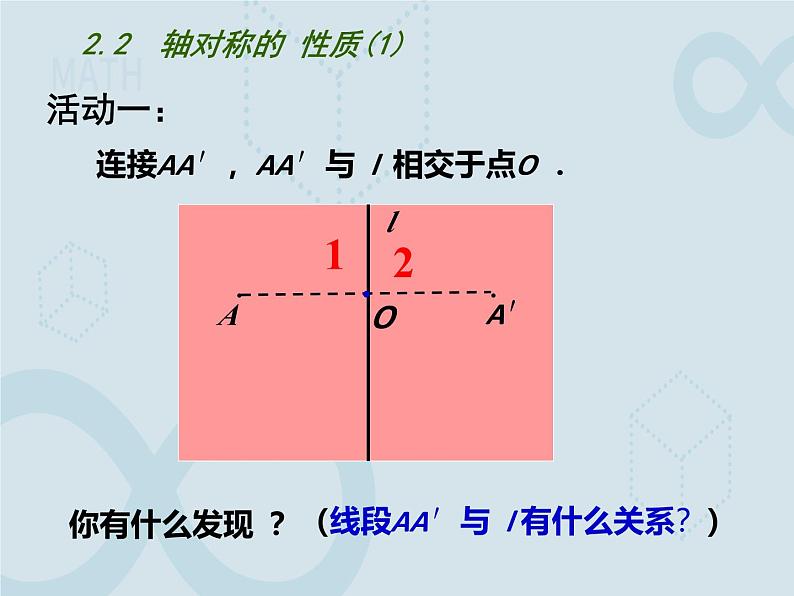
2.2　轴对称的 性质(1)
如图所示，把一张纸折叠后，用针扎一个孔（印子）；
再把纸展开，两针孔分别记为点A、点A′，折痕记为l ；
连接AA′，AA′与 l 相交于点O ．
你有什么发现 ？
（线段AA′与 l 有什么关系？）
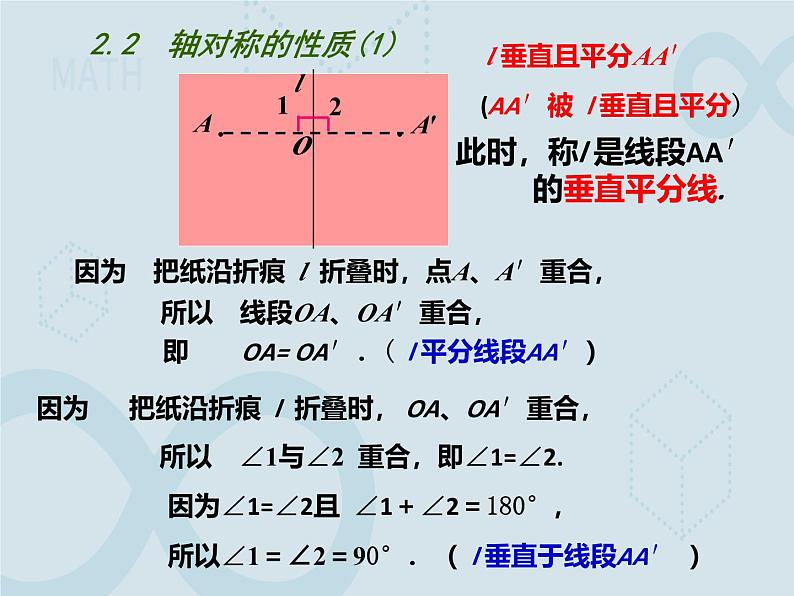
所以 线段OA、OA′重合，
所以 ∠1与∠2 重合，即∠1=∠2.
即 OA= OA′．( l 平分线段AA′）
所以∠1＝∠2＝90°．（ l 垂直于线段AA′ ）
因为 把纸沿折痕 l 折叠时，点A、A′重合，
2.2　轴对称的性质(1)
因为 把纸沿折痕 l 折叠时， OA、OA′重合，
因为∠1=∠2且 ∠1＋∠2＝180°，
(AA′被 l 垂直且平分)
此时，称l 是线段AA′ 的垂直平分线.
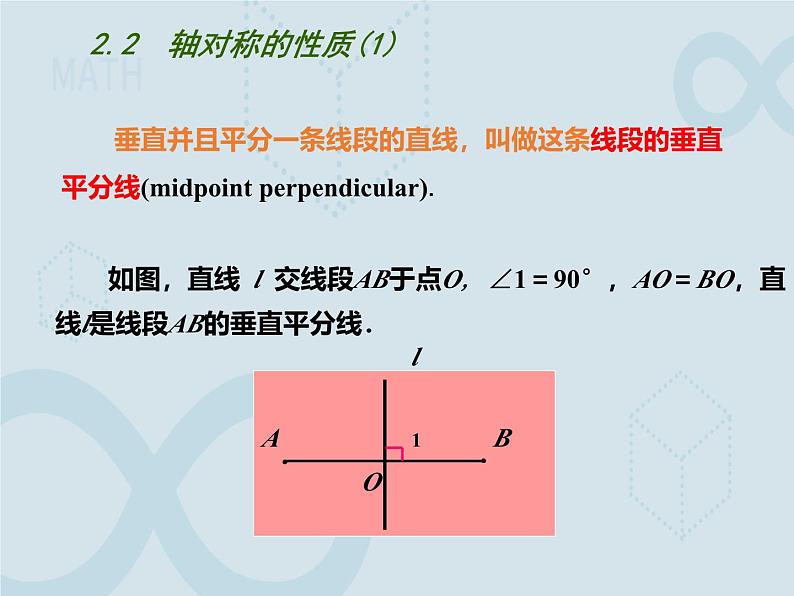
垂直并且平分一条线段的直线，叫做这条线段的垂直平分线(midpint perpendicular).
　　如图，直线 l 交线段AB于点O, ∠1＝90°，AO＝BO，直线l是线段AB的垂直平分线．
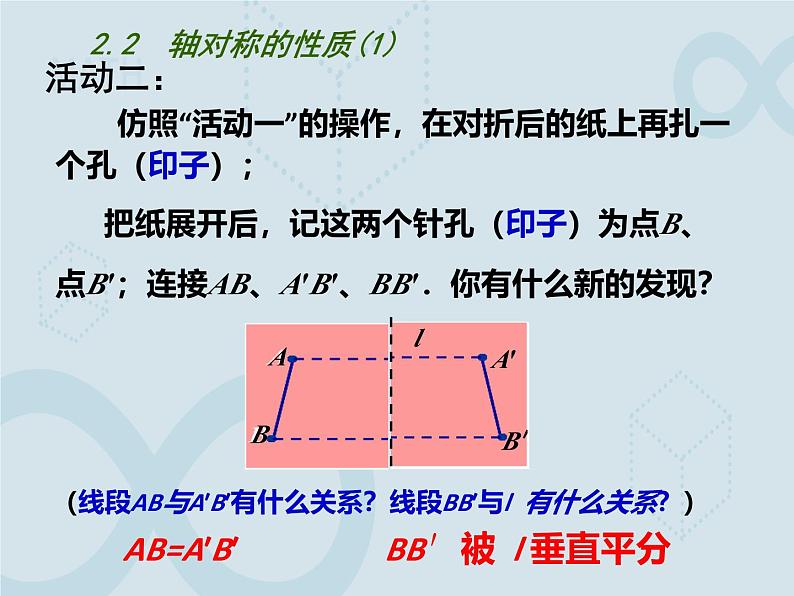
仿照“活动一”的操作，在对折后的纸上再扎一个孔（印子）； 把纸展开后，记这两个针孔（印子）为点B、点B′；连接AB、A′B′、BB′．你有什么新的发现？
（线段AB与A′B′有什么关系？线段BB′与l 有什么关系？）
BB′被 l 垂直平分
如图，并仿照上面进行操作，扎孔、展开、标记、连线．
△ABC 与△A′B′C′有什么关系？
通过上述一系列活动，你能得出什么结论？
线段CC′与l 有什么关系？
△ABC ≌ △A′B′C′
CC′被 l 垂直平分
1．成轴对称的两个图形全等．
2．成轴对称的两个图形中，对应点的连线被对称轴垂直平分．
例1　小明取一张纸，用小针在纸上扎出“4”，然后将纸放在镜子前．
(1)图中两个“4”有什么关系？
（1）你能画出镜子所在直线l的位置吗？
（2）图中点A、B、C、D的对称点分别是 ，线段AC、AB的对应线段分别是 ，CD= ， ∠CAB= ，∠ACD= .
（3）连接AE、BG， AE与BG平行吗？为什么？
因为 A和E，B和G是关于直线 l 的对称点，
所以 l⊥AE ，l⊥BG．
解：（3）平行．
（4） AE与BG平行，能说明轴对称图形对称点的连线一定互相平行吗？
解：（4） 不一定．
如图，对称点的连线DH、CF就不互相平行，而是在同一条直线上。
轴对称图形对称点的连线互相平行或在同一条直线上．
（5）延长线段CA、FE，连接CB、FG并延长，作直线AB、EG，你有什么发现吗？
　　轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行．
　　通过本节课的学习，你有什么收获？还有哪些疑惑？
（1）成轴对称的两个图形全等．
　　（2）如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线．
2．轴对称图形对称点的连线互相平行或在同一条直线上．
3．轴对称图形中的对称线段所在直线的交点在对称轴上或对称线段所在直线互相平行．