


苏科版(2024)九年级上册2.1 圆优秀课件ppt
展开1. 掌握正多边形的有关计算;
2. 掌握弧长和扇形面积的相关计算;
3. 掌握与圆有关的作图.
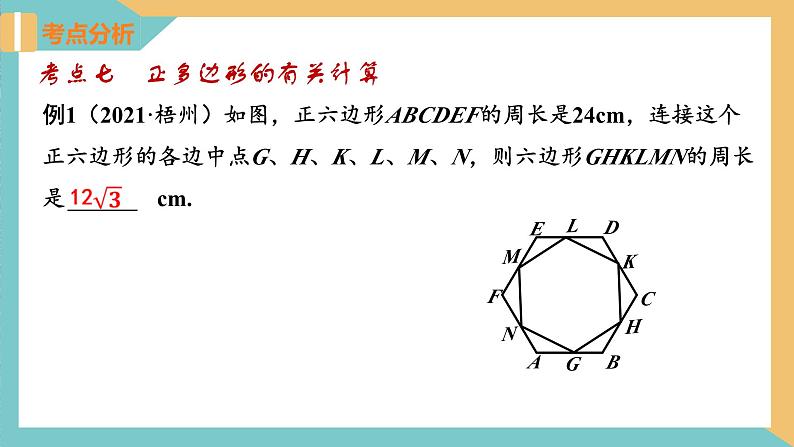
例1(2021·梧州)如图,正六边形ABCDEF的周长是24cm,连接这个正六边形的各边中点G、H、K、L、M、N,则六边形GHKLMN的周长是 ______cm.
考点七 正多边形的有关计算
1.(2023·江苏无锡)下列命题:①各边相等的多边形是正多边形;②正多边形是中心对称图形;③正六边形的外接圆半径与边长相等;④正n边形共有n条对称轴.其中真命题的个数是( ) A.4 B.3 C.2 D.1
解:各边相等各角相等的多边形是正多边形,只有各边相等的多边形不一定是正多边形,如菱形,故①是假命题;正三角形和正五边形就不是中心对称图形,故②为假命题;正六边形中由外接圆半径与边长可构成等边三角形,所以外接圆半径与边长相等,故③为真命题;根据轴对称图形的定义和正多边形的特点,可知正n边形共有n条对称轴,故④为真命题.
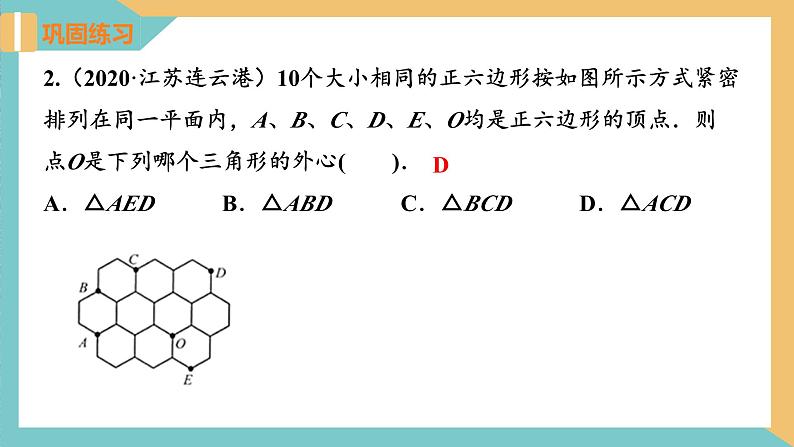
2.(2020·江苏连云港)10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点.则点O是下列哪个三角形的外心( ).A.△AED B.△ABD C.△BCD D.△ACD
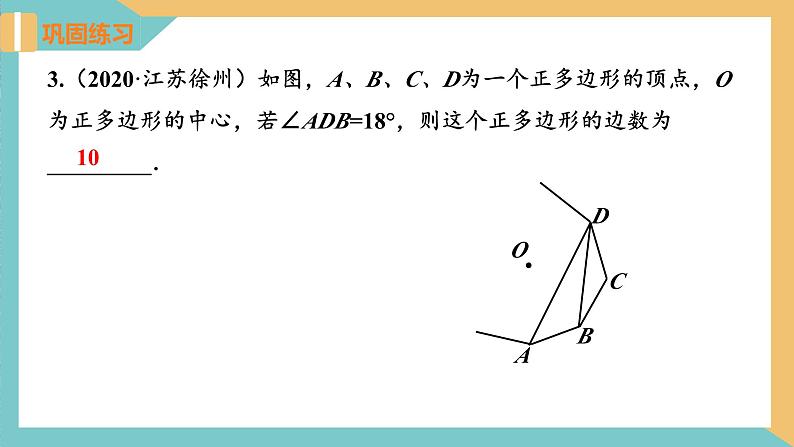
3.(2020·江苏徐州)如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为_________.
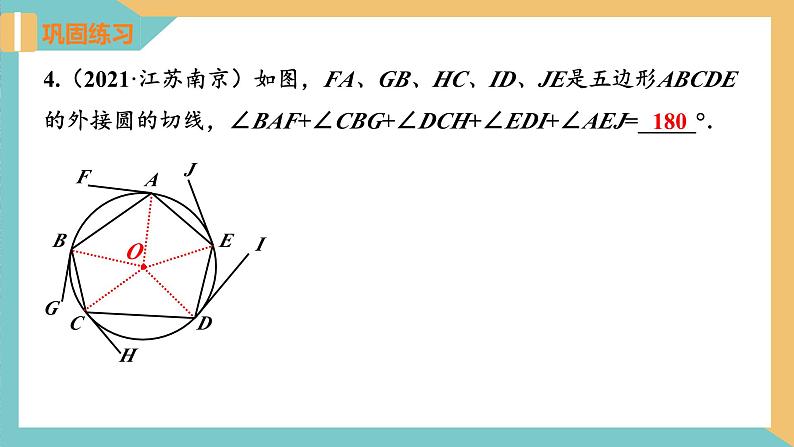
4.(2021·江苏南京)如图,FA、GB、HC、ID、JE是五边形ABCDE的外接圆的切线,∠BAF+∠CBG+∠DCH+∠EDI+∠AEJ=_____°.
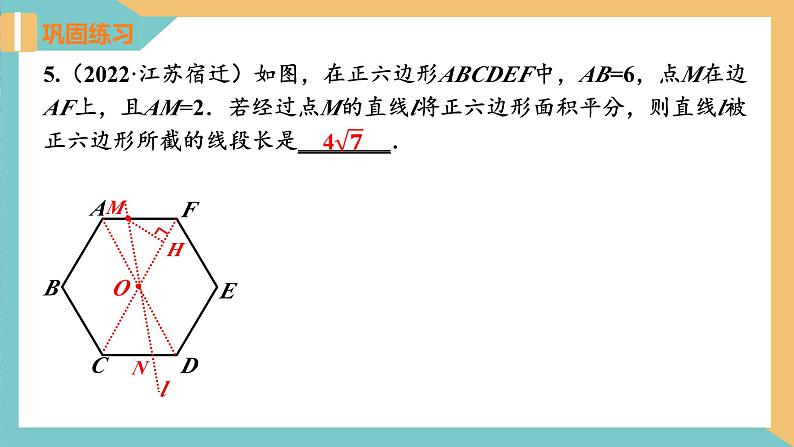
5.(2022·江苏宿迁)如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是________.
考点八 弧长和扇形面积
注意:用扇形面积公式进行计算时,要注意公式中n的意义,n表示1°圆心角的倍数,它是不带单位的.
例1 有一长为4 cm、宽为3 cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上的顶点A的位置变化为A→A1→A2,其中第二次翻滚被桌面上的一小木块挡住,使木板边沿A2C与桌面成30°角,求点A翻滚到A2位置走过的路径长.
例2 运用图形运动的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8. 求图中阴影部分的面积.
在有关圆的面积计算问题中: 如果是规则图形,那么按规则图形的面积公式去求;如果是不规则图形,那么需采用“转化”的数学思想方法,把不规则图形采用“割补法”“等积变形法” “平移法”“旋转法”等转化为规则图形,再求面积.
1.(2023·江苏连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形:乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形,下列叙述正确的是( ).
A.只有甲是扇形 B.只有乙是扇形C.只有丙是扇形 D.只有乙、丙是扇形
3.(2022·江苏连云港)如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
4.(2023·江苏扬州)用半径为24cm,面积为120πcm2的扇形纸片,围成一个圆锥的侧面,则这个圆锥的底面圆的半径为_____cm.
5.(2021·江苏南通)圆锥的母线长为2cm,底面圆的半径长为1cm,则该圆锥的侧面积为______cm2.
6.(2023·江苏徐州)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角θ=120°,则该圆锥的底面圆的半径r长为______.
例(2023·江苏徐州)两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.(1)若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为_______;
(1)解:由图1可知:璧的“肉”的面积为π(32-12)=8π;环的“肉”的面积为π(32-1.52)=6.75π,∴它们的面积之比为8π:6.75π=32:27;
考点九 与圆有关的作图
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
②按照①中作出圆的圆心O,过圆心画一条直径AB,过点A作一条射线,然后以A为圆心,适当长为半径画弧,把射线三等分,交点分别为C、D、E,连接BC,然后分别过点D、E作BC的平行线,交AB于点F、G,进而以为直径画圆,则问题得解;如图所示:
1.(2019·江苏宿迁)在Rt△ABC中,∠C=90°.(1)如图①,点O在斜边AB上,以点O为圆心,OB长为半径的圆交AB于点D,交BC于点E,与边AC相切于点F.求证:∠1=∠2;
证明:如图①,连接OF,∵AC是⊙O的切线,∴OE⊥AC,∵∠C=90°,∴OE∥BC,∴∠1=∠OFB,∵OF=OB,∴∠OFB=∠2,∴∠1=∠2.
(2)在图②中作⊙M,使它满足以下条件:①圆心在边AB上;②经过点B;③与边AC相切.(尺规作图,只保留作图痕迹,不要求写出作法)
2.如图,在△ABC中,已知AB=AC,且∠BAC<60 °,AD ⊥BC于点D.(1)在图1中,请你在AD上,仅用圆规确定E点,使∠BEC=60°;(2)在图2中,请你分别在AB、AC上,仅用圆规确定P、Q两点,使∠BPC=∠BQC=90°(作图要求:保留痕迹,不写画法).
解:(1)作以B为圆心,以BC长为半径为弧,交AD于点E;
(2)以D为圆心,BD长为半径作半圆,与AB、AC分别交于点P、Q两点.
3. P是⊙O上的一点.(1)在⊙O上求作一点B,使PB是⊙O的内接正三角形的一边;(2)在BP上求作一点A,使PA是⊙O的内接正方形的一边;
解:(1)如图①,以P为圆心,OP长为半径在⊙O上依次截取两条弧,第二条弧与⊙O的交点为B,连接PB,则PB即为所求.
(2)如图①,作直径PH,过圆心O作直径PH的垂线与BP交于点A,则PA即为所求.
(3)求作⊙O的内接正十二边形.
● M
(3)如图②,以P为圆心,OP长为半径在⊙O上依次截取6条弧得6个点,则这6个点是圆的六等分点,作各弧的中点,顺次连接12个点,得到⊙O的内接正十二边形.
苏科版九年级数学上册 小结与思考(1)(课件): 这是一份苏科版九年级上册本册综合备课ppt课件,共24页。PPT课件主要包含了创设情境,中考真题,延伸探究1,探究应用,延伸探究2,延伸探究3,谈一谈你学到了什么等内容,欢迎下载使用。
苏科版九年级数学上册 小结与思考(19)(课件): 这是一份数学九年级上册本册综合背景图课件ppt,
苏科版九年级数学上册 小结与思考(9)(课件): 这是一份初中数学苏科版九年级上册本册综合课文配套ppt课件,共9页。PPT课件主要包含了圆的有关性质,与圆有关的位置关系,圆中的计算,知识梳理,分类讨论思想,问题1,错题再现,归纳反思,例题分析,几何画板等内容,欢迎下载使用。













