人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数优秀ppt课件

这是一份人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数优秀ppt课件，共29页。PPT课件主要包含了学习目标，观察如图，0＋∞，-∞0，定义域，答案2＋∞，答案B，通性通法，关于定点问题，答案-22等内容，欢迎下载使用。

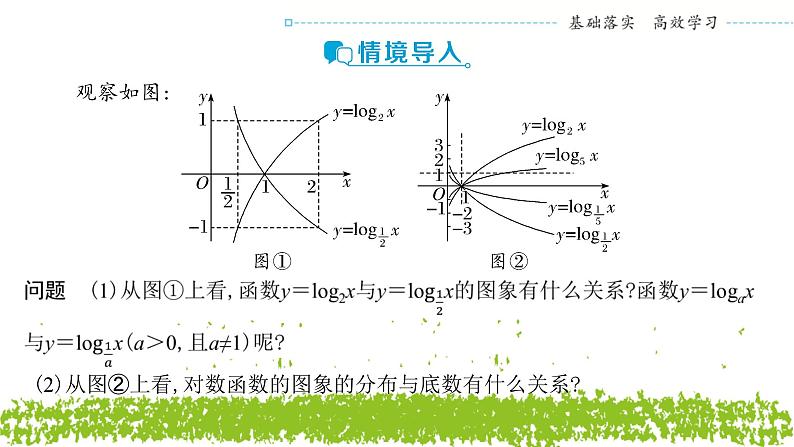
(2)从图②上看,对数函数的图象的分布与底数有什么关系?
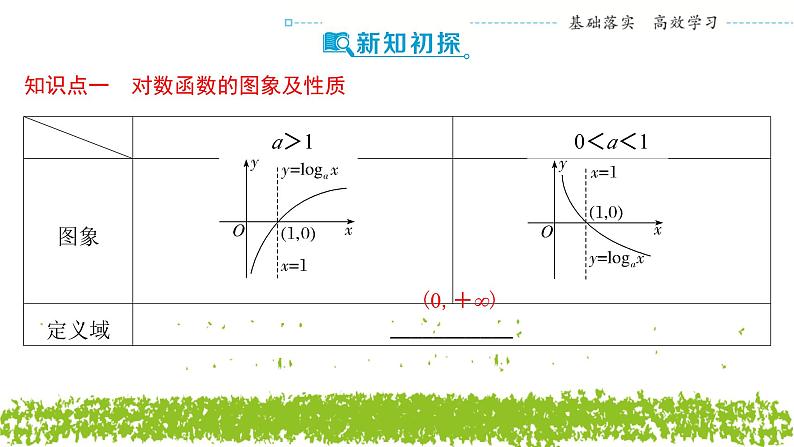
知识点一　对数函数的图象及性质
提醒　(1)函数图象只出现在y轴右侧;(2)对任意底数a,当x＝1时,y＝0,故过定点(1,0);(3)当0＜a＜1时,底数越小,图象越靠近x轴;(4)当a＞1时,底数越大,图象越靠近x轴.
知识点二　反函数　指数函数y＝ax(a＞0,且a≠1)与对数函数y＝lgax(a＞0,且a≠1)互为反函数,它们的 　定义域　⁠与 　值域　⁠正好互换.提醒　反函数性质的再理解:①互为反函数的两个函数图象关于直线y＝x对称;②反函数的定义域是原函数的值域,反函数的值域是原函数的定义域.
1.函数y＝lg(x＋1)的图象大致是(　　)
解析:C　将y＝lg x的图象向左平移1个单位得y＝lg(x＋1)的图象.
2.函数f(x)＝lga(x-1)＋1(a＞0,且a≠1)的图象恒过点(　　)
解析:C　令x-1＝1,即x＝2,得f(2)＝lga1＋1＝1,因此f(x)的图象恒过点(2,1).故选C.
4.若函数y＝lg(2a-3)x在(0,＋∞)上是增函数,则实数a的取值范围是 　　　　⁠. 
解析:由题意,得2a-3＞1,解得a＞2.所以a的取值范围是(2,＋∞).
【例1】　(1)如图,若C1,C2分别为函数y＝lgax和y＝lgbx的图象,则(　　)
(1)解析　作直线y＝1,则直线与C1,C2的交点的横坐标分别为a,b,易知0＜b＜a＜1.
∴函数y＝lg5｜x｜的图象如图所示:
(2)已知f(x)＝lga｜x｜,满足f(-5)＝1,试画出函数f(x)的图象.
(变设问)在本例(2)中,若条件不变,试画出函数h(x)＝｜lgax｜的图象.
解:因为a＝5,所以h(x)＝｜lg5x｜.h(x)的图象如图中实线部分所示.
1.对数函数底数对图象的影响
其中a,b,c,d是图象对应的对数函数的底数,根据图象,其大小关系为0＜c＜d＜1＜a＜b.
求函数y＝m＋lgaf(x)(a＞0,且a≠1)的图象过定点时,只需令f(x)＝1求出x,即得定点为(x,m).
1.函数f(x)＝lga｜x｜＋1(a＞1)的图象大致为(　　)
解析:C　∵函数f(x)＝lga｜x｜＋1(a＞1)是偶函数,∴f(x)的图象关于y轴对称,当x＞0时,f(x)＝lgax＋1单调递增;当x＜0时,f(x)＝lga(-x)＋1单调递减, 又∵函数f(x)的图象过(1,1),(-1,1)两点,∴结合选项可知选项C中的图象符合题意.
2.若函数y＝lga(x＋b)＋c(a＞0,且a≠1)的图象恒过定点(3,2),则实数b＝ 　　　　⁠,c＝ 　　　　⁠. 
【例2】　比较下列各题中两个值的大小:
(1)lg31.9,lg32;
解　(1)因为y＝lg3x在(0,＋∞)上是增函数,且1.9＜2,所以lg31.9＜lg32.
(3)lg23,lg0.32;
解　(3)因为lg23＞lg21＝0,lg0.32＜lg0.31＝0,所以lg23＞lg0.32.
(4)lgaπ,lga3.14(a＞0,且a≠1).
解　(4)π＞3.14,当a＞1时,函数y＝lgax在(0,＋∞)上是增函数,有lgaπ＞lga3.14;当0＜a＜1时,函数y＝lgax在(0,＋∞)上是减函数,有lgaπ＜lga3.14.综上可得,当a＞1时,lgaπ＞lga3.14;当0＜a＜1时,lgaπ＜lga3.14.
通性通法比较对数值大小时常用的4种方法(1)若底数为同一常数,则可由对数函数的单调性直接进行比较;(2)若底数为同一字母,则根据底数对对数函数单调性的影响,对底数进行分类讨论;(3)若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较,也可以利用顺时针方向底数增大画出对数函数的图象,再进行比较;(4)若底数与真数都不同,则常借助1,0等中间量进行比较.
下列式子中成立的是(　　)
解析:D　因为f(x)＝lg0.4x为减函数,故lg0.44＞lg0.46,故A错;因为f(x)＝1.01x为增函数,所以1.013.4＜1.013.5,故B错;由指数函数图象特点知,3.50.3＞3.40.3,故C错.设函数f(x)＝lg7x,g(x)＝lg6x,则这两个函数在定义域内都是增函数,所以lg76＜lg77＝1＝lg66＜lg67,所以D正确.
【例3】　解下列不等式:
对数不等式的三种考查类型及解法
(1)形如lgax＞lgab的不等式,借助y＝lgax的单调性求解,如果a的取值不确定,需分a＞1与0＜a＜1两种情况进行讨论;
(2)形如lgax＞b的不等式,应将b化为以a为底数的对数式的形式(b＝lgaab),再借助y＝lgax的单调性求解;
(3)形如lgf(x)a＞lgg(x)a(f(x),g(x)＞0且不等于1,a＞0)的不等式,可利用换底公式化为同底的对数进行求解,或利用函数图象求解.
(1)lg2(2x＋3)≥lg2(5x-6);
(2)lga(2x-5)＞lga(x-1).
（1）对数函数有哪些性质？结合图象说明。（2）我们可以通过哪些方式来探究对数函数的图象及性质？（3）在探究对数函数的图像及性质的过程中， 我们应用了哪些数学思想与方法？ 你还想探究关于对数函数的哪些问题？
2.下列选项正确的是(　　)