2024春高中数学第六章平面向量及其应用章末素养提升课件（人教A版必修第二册）

这是一份2024春高中数学第六章平面向量及其应用章末素养提升课件（人教A版必修第二册），共50页。
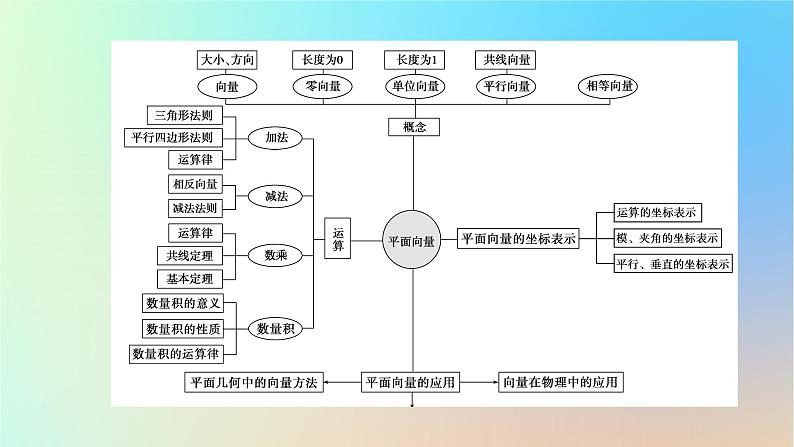
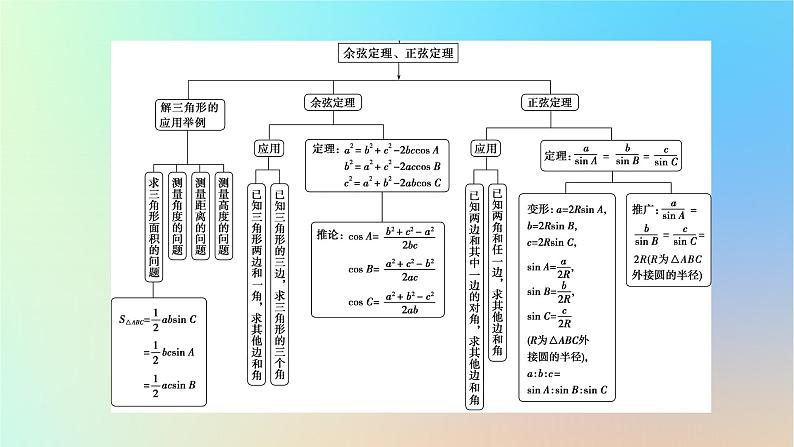
第六章　平面向量及其应用章末素养提升| 体 系 构 建 | | 核 心 归 纳 | 1．五种常见的向量(1)单位向量：模为1的向量．(2)零向量：模为0的向量．(3)平行(共线)向量：方向相同或相反的非零向量．(4)相等向量：模相等，方向相同的向量．(5)相反向量：模相等，方向相反的向量．2．两个重要定理(1)向量共线定理：向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ，使b＝λa．(2)平面向量基本定理：如果e1，e2是同一个平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a＝λ1e1＋λ2e2，其中{e1，e2}是一个基底．3．两个非零向量平行、垂直的等价条件若a＝(x1，y1)，b＝(x2，y2)，则：(1)a∥b⇔a＝λb(λ≠0)⇔x1y2－x2y1＝0；(2)a⊥b⇔a·b＝0⇔x1x2＋y1y2＝0．5．投影向量与向量b同向的单位向量为e，向量a与b的夹角为θ，则向量a在向量b上的投影向量为|a|cos θ· e．6．向量的运算律(1)交换律：a＋b＝b＋a，a·b＝b·a．(2)结合律：a＋b＋c＝(a＋b)＋c，a－b－c＝a－(b＋c)，(λa)·b＝λ(a·b)＝a·(λb)．(3)分配律：(λ＋μ)a＝λa＋μa，λ(a＋b)＝λa＋λb，(a＋b)·c＝a·c＋b·c．(4)重要公式：(a＋b)·(a－b)＝a2－b2，(a±b)2＝a2±2a·b＋b2．8．余弦定理及其推论(1)a2＝b2＋c2－2bc cos A，b2＝c2＋a2－2ca cos B，c2＝a2＋b2－2ab cos C．(3)在△ABC中，c2＝a2＋b2⇔C为直角；c2＞a2＋b2⇔C为钝角；c2＜a2＋b2⇔C为锐角．| 思 想 方 法 | (一)函数与方程思想【思想方法解读】函数与方程思想在平面向量中的应用主要是利用平面向量共线或垂直的线性运算或坐标运算，建立关于参数的方程，从而求出参数的值．平面向量中有关模、夹角的计算，常转化为函数关系，利用函数的性质求解．　　　　设0＜|a|≤2，f(x)＝cos2x－|a|sinx－|b|的最大值为0，最小值为－4，且a与b的夹角为45°，求|a＋b|．【答案】A(二)数形结合思想【思想方法解读】向量是一个有“形”的几何量，因此数形结合法适用于已知平面几何图形或向量等式，利用向量的模的几何意义，求解模的最值或取值范围等问题．【答案】(1)D　(2)B(三)化归与转化思想【思想方法解读】(1)用向量方法解决平面几何中的夹角与垂直问题的关键在于：选用适当向量为基底，把所要研究的问题转化为两向量的夹角与垂直问题，再利用向量知识求角．【答案】B3．设|a|＝|b|＝1，|3a－2b|＝3，求|3a＋b|的值．| 链 接 高 考 | 【答案】C向量的数量积【答案】11【点评】本题主要考查平面向量的数量积的定义、平面向量的运算法则等知识，属于中档题．　　　　(2022年乙卷)已知向量a＝(2，1)，b＝(－2，4)，则|a－b|＝ (　　)A．2 B．3 C．4 D．5【答案】D向量的模【点评】本题考查平面向量的坐标运算，考查向量模的求法，是基础题．　　　　(2022年新高考Ⅰ)已知向量a＝(1，1)，b＝(1，－1)．若(a＋λb)⊥(a＋μb)，则 (　　)A．λ＋μ＝1 B．λ＋μ＝－1C．λμ＝1 D．λμ＝－1【答案】D向量的垂直与夹角【解析】∵a＝(1，1)，b＝(1，－1)，∴a＋λb＝(λ＋1，1－λ)，a＋μb＝(μ＋1，1－μ)．由(a＋λb)⊥(a＋μb)，得(λ＋1)(μ＋1)＋(1－λ)(1－μ)＝0，整理得2λμ＋2＝0，即λμ＝－1．故选D．【点评】本题考查平面向量加法与数乘的坐标运算，考查两向量垂直与数量积的关系，是基础题．　　　　(2022年新高考Ⅱ)已知向量a＝(3，4)，b＝(1，0)，c＝a＋tb，若〈a，c〉＝〈b，c〉，则t＝ (　　)A．－6 B．－5 C．5 D．6【答案】C【点评】本题考查实数值的求法，考查向量坐标运算法则、向量夹角余弦公式等基础知识以及运算求解能力，属于基础题．　　　　(2023年乙卷)在△ABC中，已知∠BAC＝120°，AB＝2，AC＝1．(1)求sin ∠ABC；(2)若D为BC上一点，且∠BAD＝90°，求△ADC的面积．正、余弦定理的应用【点评】本题考查余弦定理的应用、三角形面积的计算，属基础题．　　　　 (2022年乙卷)记△ABC的内角A，B，C的对边分别为a，b，c，已知sin C sin (A－B)＝sin B sin (C－A)．(1)若A＝2B，求C；(2)求证：2a2＝b2＋c2．(1)解：由sin C sin (A－B)＝sin B sin (C－A)，又∵A＝2B，∴sin C sin B＝sin B sin (C－A)．∵sin B≠0，∴sin C＝sin (C－A)，即C＝C－A(舍去)或C＋C－A＝π．(2)证明：由sin C sin (A－B)＝sin B sin (C－A)，得sin C sin A cos B－sin C cos A sin B＝sin B sin C cos A－sin Bcos C sin A，由正弦定理可得ac cos B－bc cos A＝bc cos A－ab cos C，【点评】本题考查三角形的解法、正弦定理与余弦定理的应用以及运算求解能力，属于中档题．【点评】本题考查倍角公式、和差公式、三角形内角和定理、余弦定理、基本不等式、转化方法以及推理能力与计算能力，属于中档题．