2021学年8.1 基本立体图形教案配套课件ppt

这是一份2021学年8.1 基本立体图形教案配套课件ppt，共25页。PPT课件主要包含了新知梳理，旋转轴叫做圆柱的轴，旋转轴叫做圆锥的轴，旋转轴叫做圆台的轴，典例分析，课堂小结，课后作业等内容，欢迎下载使用。

1、一般地，由若干个平面多边形围成的几何体叫做多面体.
（1）棱柱：一般地，有两个面互相平行，其余各面都是四边形，并 且相邻两个四边形的公共边都互相平行，由这些面所围成的多 面体叫做棱柱.
（2）棱锥：一般地，有一个面是多边形，其余各面都是有一个公 共顶点的三角形，由这些面所围成的多面体叫做棱锥.
（3）棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面 之间的部分叫做棱台.
2、一条平面曲线（包括直线）绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面，封闭的旋转面围成的几何体叫做旋转体.
思考：圆柱是由什么平面图形旋转形成的？圆柱.gsp
定义：以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱.
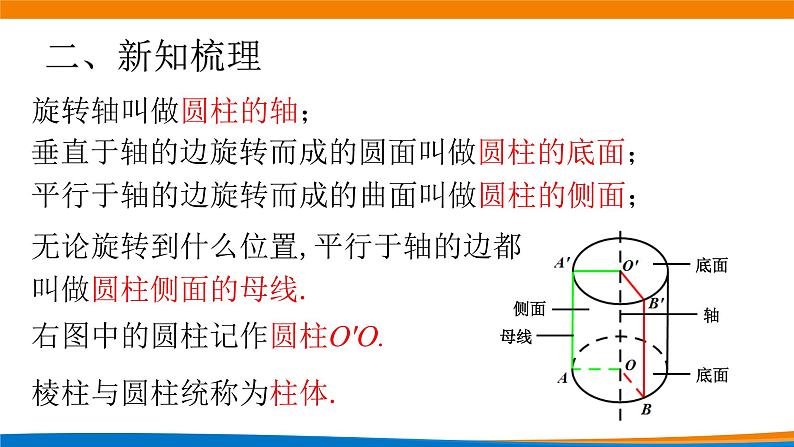
垂直于轴的边旋转而成的圆面叫做圆柱的底面；
平行于轴的边旋转而成的曲面叫做圆柱的侧面；
无论旋转到什么位置,平行于轴的边都叫做圆柱侧面的母线.
右图中的圆柱记作圆柱O'O.
棱柱与圆柱统称为柱体.
思考：圆锥是由什么平面图形旋转形成的？圆锥.gsp
定义：以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
直角三角形另一条直角边旋转而成的圆面叫做圆锥的底面；
斜边旋转而成的曲面叫做圆锥的侧面；
无论旋转到什么位置,直角三角形的斜边都叫做圆锥侧面的母线.
棱锥与圆锥统称为锥体.
右图可表示为圆锥SO .
思考：圆台是如何定义的？
定义：用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
思考：圆柱可以由矩形旋转得到，圆锥可以由直角三角形旋转得到，圆台是否也可以由平面图形旋转得到？如果可以，由什么平面图形旋转得到？如何旋转？圆台.gsp
直角梯形上、下底旋转而成的圆面叫做圆台的上、下底面；
不垂直底边的腰旋转而成的曲面叫做圆台的侧面；
无论旋转到什么位置,直角梯形中不垂直底边的腰都叫做圆台侧面的母线.
棱台与圆台统称为台体.
右图的圆台可表示为圆台O'O .
思考：球是由什么平面图形旋转形成的？球.gsp
定义：半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球.
半圆的圆心叫做球的球心,
连接球心和球面上任意一点的线段叫做球的半径,
连接球面上两点并且经过球心的线段叫做球的直径.
球常用表示球心的字母来表示,右图可表示为球O .
探究：圆柱、圆锥、圆台都是旋转体，当底面发生变化时，它们能否互相转化？
当圆台的上底面扩大，和下底面全等时，就是圆柱；当圆台上底面缩为一点时，就是圆锥.
棱柱、棱锥、棱台、圆柱、圆锥、圆台和球是常见的简单几何体.
由简单几何体组合而成的几何体称作简单组合体.
简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成;另一种是由简单几何体截去或挖去一部分而成.
1、旋转体：圆柱、圆锥、圆台、球2、简单组合体：由简单几何体拼接而成；由简单几何体截去或挖去一部分而成.
教材104页练习；105-106页习题8.1第3，4，5，9题。