





还剩48页未读,
继续阅读
第2章 轴对称图形 小结与思考 苏科版八年级数学上册课件
展开
这是一份第2章 轴对称图形 小结与思考 苏科版八年级数学上册课件,共56页。
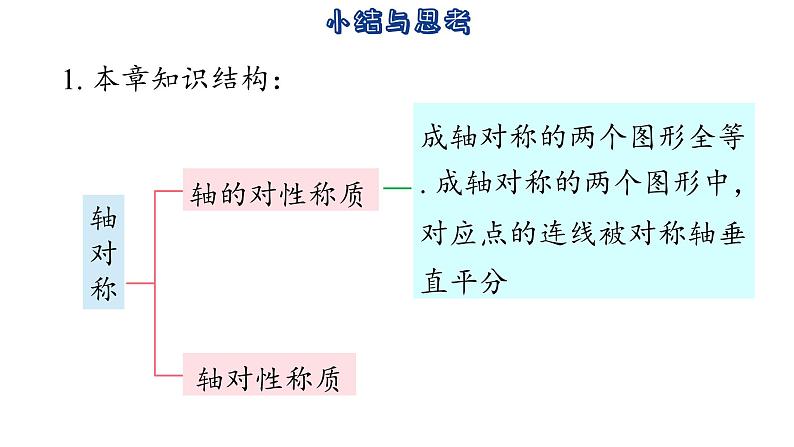
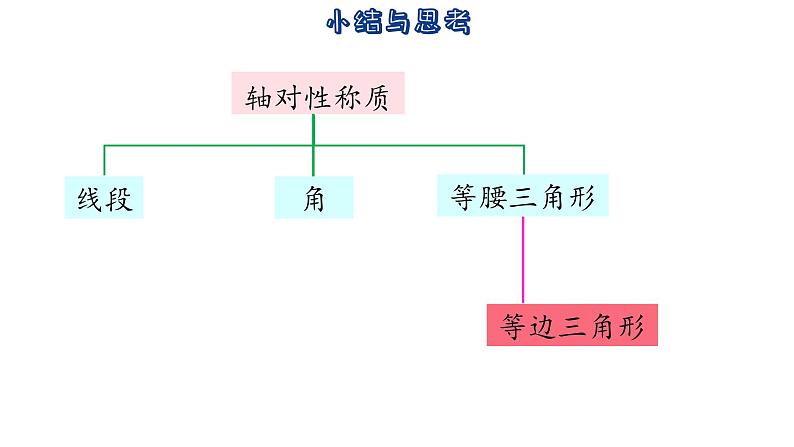
第2章 轴对称图形小结与思考 1. 本章知识结构:轴对称轴的对性称质轴对性称质轴对性称质线段角等腰三角形等边三角形线段线段的垂直平分线是它的对称轴线段垂直平分线上的点到线段两端的距离相等到线段两端距离相等的点在线段的垂直平分线上角角平分线所在直线是它的对称轴角平分线上的点到角 两边的离相等角的内部到角两边距离相等的点在角的平分线上等腰三角形顶角平分线所在直线是它的对称轴等腰三角形的两底角相等。等腰三角形底边上的高线、中线及顶角平分线重合有两个角相等的三角形是等腰三角形直角三角形斜边上的中线等于斜边的一半等边三角形角平分线所在直线它的对称轴等边三角形的各角都等于 60° 三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形2. 说说轴对称与轴对称图形的区别和联系. 3.“等腰三角形的两底角相等”揭示了等腰三角形具有的一个性质,称为等腰三角形的性质定理;“有两个角相等的三角形是等腰三角形”揭示了具备什么条件的三角形是等腰三角形,称为等腰三角形的判定定理. 这两个定理是互逆定理. 你能在学过的定理中,再说出一对互逆定理,并指出其中哪一个是性质定理,哪一个是判定定理吗? 4. 在本章学习中,通过图形的翻折,探索并证实了线段的垂直平分线、角平分线、等腰三角形的性质. 运用图形运动的方法,也可以研究图形的性质. 5. 本章例题中的“思考与表述”,体现了“由未知想须知”的思路,这是我们探索解决问题途径常用的一种思考方法.复习题1.下列图形是不是轴对称图形?如果是,画出它的对称轴. 解:图③不是轴对称图形,图①②④是轴对称图形,画对称轴略.2. 请查找一些国家的国旗图案,并指出其中哪些是轴对 称图形?试分别找出它们的对称轴.略3. (1) 图①是轴对称图形吗?如果是,它有几条对称轴? 如果不是可以怎样把它补成轴对称图形? 解:图①不是轴对称图形,只要把拐角处“断开”部分连接起来,即可补成轴对称图形,如图所示.(2) 图②由5张全等的正方形纸片组成,只移动其中1张 纸片,你能使它变成轴对称图形吗?能,如图所示. (答案不唯一)4. 如图,在△ABC中,AB= AC, D是BC的中点,AC 的垂直平 分线分别交 AC、AD、AB 于 点E、F、G. 点F到△ABC的边 __________的距离相等,点F 到△ABC的顶点___________ 的距离相等.AB,ACA,B,C5. (1) 在等腰三角形ABC中,∠A=80°. 若∠A是顶角,则∠B= _________°; 若∠B是顶角,则∠B= _________°; 若∠C是顶角,则∠B= _________°.502080(2) 等腰三角形ABC的周长为8 cm,AB=3cm. 若AB是底边,则BC= ________ cm; 若_________,则BC =________ cm; 若_________ ,则BC= ________cm.2.5BC是底边2AC是底边36. 在如图的网格中: (1)画△A1B1C1,使它与△ABC 关于l1对称; (2)画△A2B2C2,使它与△A1B1C1关于l2对称; (3) 画△A3B3C3,使它与△A2B2C2关于l3对称; (4) 画出△A3B3C3与△ABC 的对称轴.7. 根据下列已知条件,分别指出各个图形中的等腰三 角形,并加以证明, (1) 如图①,BD平分∠ABC,点 E 在BC 上,且 DE∥AB;解:△BED是等腰三角形.证明如下:∵BD 平分∠ABC, ∴∠ABD=∠CBD. ∵DE∥AB, ∴∠BDE=∠ABD. ∴∠CBD=∠BDE, ∴EB=ED(等角对等边), ∴△BED 是等腰三角形.(2) 如图②,AD平分∠BAC,点E在BA的 延长线上,且 EC//AD;解:△ACE 是等腰三角形.证明如下: ∵AD 平分∠BAC, ∴∠BAD = ∠CAD. ∵EC∥AD, ∴∠BAD =∠E, ∠CAD =∠ACE.∴∠E=∠ACE,∴AC=AE (等角对等边),∴△ACE 是等腰三角形.(3) 如图③,AD平分∠BAC,点E在 BD 上,点G在CA 的延长线上, 且GE∥AD,GE交AB 于点F.解:△AGF是等腰三角形.证明如下: ∵AD 平分∠BAC, ∴∠BAD=∠CAD. ∵GE∥AD,∴∠G=∠CAD,∠AFG=∠BAD.∴∠G=∠AFG,∴ AG=AF(等角对等边),∴△AGF 为等腰三角形.8. 已知:如图,在△ABC 中,∠ABC、∠ACB的平分线 相交于点O,MN 过点O,且 MN ∥BC,分别 交AB、AC 于点M、N. 求证:MN=BM+CN.证明:∵BO 平分∠ABC, ∴∠MBO=∠CBO. ∵MN∥BC, ∴∠MOB=∠CBO. ∴∠MBO=∠MOB, ∴BM=MO(等角对等边). 同理 CN=NO. ∴MN=MO+NO=BM+CN.9. 如图,点 D、E 在 BC 上,且AB=AC,AD=AE. 图中 还有哪些相等的线段?试用不同的方法证明你的结论。解:BD=CE,BE=CD.方法一: ∵AB=AC,AD=AE, ∴∠B=∠C,∠ADE=∠AED.10. 已知:如图,∠ABC =∠ADC=90°,M、N 分别 是 AC、BD 的中点. 求证:MN⊥BD.证明:如图,连接 BM,DM.11. (1) 野营活动中,小明用一块等腰三角形的铁皮代替 锅,烙一块与铁皮形状、大小相同的饼,烙好一 面后把饼翻身,这块饼仍能正好落在“锅”中, 这是为什么? 解:因为烙的饼与“锅(铁皮)”是全等的等腰三角形,而等腰三角形是轴对称图形,所以把饼翻身后会正好落在“锅”中. (2) 小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、大小相同的饼,如果烙好一面后就把饼翻身,那么这块饼不能正好落在“锅”中. 小丽将饼切了一刀,然后将两小块都翻身,结果饼就能正好落在“锅”中. 小丽怎样切的? 为什么? 解:小丽将其沿直角三角形斜边中线分开为两个三角形,这两个三角形都是等腰三角形,如图所示的△ACD与△BCD,因此由(1)知“翻身后能与原图形重合,故还是能正好落在“锅”中. (3) 如果用来烙饼的铁皮既不是等腰三角形也不是直角三角形 (如图②),那么烙好一面后,怎样将烙饼翻身,才能使烙饼仍能正好落在“锅”中? 解:如图所示,作△ABC 的高AD,把△ABC 分成两个直角三角形,根据(2)中的方法,再作边AB,AC 的中线DE,DF. 因此,共切3刀:AD,DE,DF,或者只切2刀,即只要找出图中的 D点所在的位置,只需切 DE,DF,图中四边形AEDF 是轴对称图形,“翻身”后仍能与原来重合. 12. 在一个三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形吗?证明你的结论. 13,如图,AB=AC=AD. (1) 如果 AD∥BC,那么∠C和∠D有 怎样的数量关系?证明你的结论;解:∠C=2∠D.证明如下: ∵AD∥BC, ∴∠DBC=∠D. ∵AB=AD, ∴∠D=∠ABD,∴∠ABC=2∠D.∵AB=AC,∴∠ABC=∠C.∴∠C=2∠D.(2) 如果∠C=2∠D,那么你能得到 什么结论?证明你的结论解:AD∥BC. 证明如下: ∵AB=AC, ∴∠C=∠ABC=2∠D. ∵AB=AD, ∴∠ABD=∠D.∵∠ABC=2∠D.∴∠CBD=∠D.∴AD∥BC.14. (1) 如图,在△ABC中,∠BAC=90°,AB=AC, 点D在 BC 上且BD=BA,点E在BC的延长线上, 且CE=CA,求∠DAE的度数; (2) 如果把第(1)题中“AB=AC”的条件舍去,其余条件 不变,那么∠DAE的度数会改变吗? 解:∠DAE 的度数不会改变.如图所示.∵BD=BA,∠BAC=90°,∴∠4=∠BAD=90°-∠1.∵CA=CE,∴∠2=∠E.又∵∠4=∠1+∠3, ∠3=∠2+∠E,∴∠3=2∠2,∴∠4=90°-∠1=∠1+2∠2,∴2∠1+2∠2=90°,∴2(∠1+∠2)=90°,∴∠1+∠2=45°,∴∠DAE=45°,∴∠DAE 的度数不会改变.(3) 如果把第(1)题中“∠BAC=90°”的条件改为 “∠BAC=90°”,其余条件不变,那么∠DAE 与∠BAC 有怎样的数量关系? 解:∠BAC 的度数是∠DAE 度数的2倍.如图所示∵BA=BD,∴∠BAD=∠4,∴∠BAC=∠BAD+∠1=∠4+∠1.又∵∠4=∠1+∠3,CA=CE,∴∠2=∠E,∴∠3=2∠2,∴∠BAC=∠1+∠4 = ∠1+∠1+2∠2 =2(∠1+∠2).又∵∠DAE=∠1+∠2.∴∠BAC=2∠DAE.∴∠BAC 的度数是∠DAE 度数的2倍.15. 我们知道:如果点P在线段AB 的垂直平分线l上,那 么PA=PB;如果 PA=PB,那么点P在线段AB 的垂直 平分线l上;如果点P不在线段AB 的垂直平分线l上, 那么 PA≠PB. 试证明:如果 PA≠PB,那么点P不在 线段AB的垂直平分线l上. 证明:假设点P在线段AB的垂直平分线上,由线段垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”得 PA=PB,这与PA≠PB 相矛盾,所以点 P 不在线段AB 的垂直平分线上.16. 已知直线l、点A和点B. 试在直线l上确定一点P,使 PA+PB最小.若点 A,B 在直线l的异侧:如图 4,5,6. 如图2,点A,B到直线的距离相等,线段AB的垂直平分线与直线l的交点为 P,则此时PA+PB最小; 如图 3,点A,B 所在直线垂直于直线l,垂足为P,则此时 PA+PB 最小. 如图 4,5,6,线段 AB 与直线的交点为P,则此时PA+PB 最小.
第2章 轴对称图形小结与思考 1. 本章知识结构:轴对称轴的对性称质轴对性称质轴对性称质线段角等腰三角形等边三角形线段线段的垂直平分线是它的对称轴线段垂直平分线上的点到线段两端的距离相等到线段两端距离相等的点在线段的垂直平分线上角角平分线所在直线是它的对称轴角平分线上的点到角 两边的离相等角的内部到角两边距离相等的点在角的平分线上等腰三角形顶角平分线所在直线是它的对称轴等腰三角形的两底角相等。等腰三角形底边上的高线、中线及顶角平分线重合有两个角相等的三角形是等腰三角形直角三角形斜边上的中线等于斜边的一半等边三角形角平分线所在直线它的对称轴等边三角形的各角都等于 60° 三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形2. 说说轴对称与轴对称图形的区别和联系. 3.“等腰三角形的两底角相等”揭示了等腰三角形具有的一个性质,称为等腰三角形的性质定理;“有两个角相等的三角形是等腰三角形”揭示了具备什么条件的三角形是等腰三角形,称为等腰三角形的判定定理. 这两个定理是互逆定理. 你能在学过的定理中,再说出一对互逆定理,并指出其中哪一个是性质定理,哪一个是判定定理吗? 4. 在本章学习中,通过图形的翻折,探索并证实了线段的垂直平分线、角平分线、等腰三角形的性质. 运用图形运动的方法,也可以研究图形的性质. 5. 本章例题中的“思考与表述”,体现了“由未知想须知”的思路,这是我们探索解决问题途径常用的一种思考方法.复习题1.下列图形是不是轴对称图形?如果是,画出它的对称轴. 解:图③不是轴对称图形,图①②④是轴对称图形,画对称轴略.2. 请查找一些国家的国旗图案,并指出其中哪些是轴对 称图形?试分别找出它们的对称轴.略3. (1) 图①是轴对称图形吗?如果是,它有几条对称轴? 如果不是可以怎样把它补成轴对称图形? 解:图①不是轴对称图形,只要把拐角处“断开”部分连接起来,即可补成轴对称图形,如图所示.(2) 图②由5张全等的正方形纸片组成,只移动其中1张 纸片,你能使它变成轴对称图形吗?能,如图所示. (答案不唯一)4. 如图,在△ABC中,AB= AC, D是BC的中点,AC 的垂直平 分线分别交 AC、AD、AB 于 点E、F、G. 点F到△ABC的边 __________的距离相等,点F 到△ABC的顶点___________ 的距离相等.AB,ACA,B,C5. (1) 在等腰三角形ABC中,∠A=80°. 若∠A是顶角,则∠B= _________°; 若∠B是顶角,则∠B= _________°; 若∠C是顶角,则∠B= _________°.502080(2) 等腰三角形ABC的周长为8 cm,AB=3cm. 若AB是底边,则BC= ________ cm; 若_________,则BC =________ cm; 若_________ ,则BC= ________cm.2.5BC是底边2AC是底边36. 在如图的网格中: (1)画△A1B1C1,使它与△ABC 关于l1对称; (2)画△A2B2C2,使它与△A1B1C1关于l2对称; (3) 画△A3B3C3,使它与△A2B2C2关于l3对称; (4) 画出△A3B3C3与△ABC 的对称轴.7. 根据下列已知条件,分别指出各个图形中的等腰三 角形,并加以证明, (1) 如图①,BD平分∠ABC,点 E 在BC 上,且 DE∥AB;解:△BED是等腰三角形.证明如下:∵BD 平分∠ABC, ∴∠ABD=∠CBD. ∵DE∥AB, ∴∠BDE=∠ABD. ∴∠CBD=∠BDE, ∴EB=ED(等角对等边), ∴△BED 是等腰三角形.(2) 如图②,AD平分∠BAC,点E在BA的 延长线上,且 EC//AD;解:△ACE 是等腰三角形.证明如下: ∵AD 平分∠BAC, ∴∠BAD = ∠CAD. ∵EC∥AD, ∴∠BAD =∠E, ∠CAD =∠ACE.∴∠E=∠ACE,∴AC=AE (等角对等边),∴△ACE 是等腰三角形.(3) 如图③,AD平分∠BAC,点E在 BD 上,点G在CA 的延长线上, 且GE∥AD,GE交AB 于点F.解:△AGF是等腰三角形.证明如下: ∵AD 平分∠BAC, ∴∠BAD=∠CAD. ∵GE∥AD,∴∠G=∠CAD,∠AFG=∠BAD.∴∠G=∠AFG,∴ AG=AF(等角对等边),∴△AGF 为等腰三角形.8. 已知:如图,在△ABC 中,∠ABC、∠ACB的平分线 相交于点O,MN 过点O,且 MN ∥BC,分别 交AB、AC 于点M、N. 求证:MN=BM+CN.证明:∵BO 平分∠ABC, ∴∠MBO=∠CBO. ∵MN∥BC, ∴∠MOB=∠CBO. ∴∠MBO=∠MOB, ∴BM=MO(等角对等边). 同理 CN=NO. ∴MN=MO+NO=BM+CN.9. 如图,点 D、E 在 BC 上,且AB=AC,AD=AE. 图中 还有哪些相等的线段?试用不同的方法证明你的结论。解:BD=CE,BE=CD.方法一: ∵AB=AC,AD=AE, ∴∠B=∠C,∠ADE=∠AED.10. 已知:如图,∠ABC =∠ADC=90°,M、N 分别 是 AC、BD 的中点. 求证:MN⊥BD.证明:如图,连接 BM,DM.11. (1) 野营活动中,小明用一块等腰三角形的铁皮代替 锅,烙一块与铁皮形状、大小相同的饼,烙好一 面后把饼翻身,这块饼仍能正好落在“锅”中, 这是为什么? 解:因为烙的饼与“锅(铁皮)”是全等的等腰三角形,而等腰三角形是轴对称图形,所以把饼翻身后会正好落在“锅”中. (2) 小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、大小相同的饼,如果烙好一面后就把饼翻身,那么这块饼不能正好落在“锅”中. 小丽将饼切了一刀,然后将两小块都翻身,结果饼就能正好落在“锅”中. 小丽怎样切的? 为什么? 解:小丽将其沿直角三角形斜边中线分开为两个三角形,这两个三角形都是等腰三角形,如图所示的△ACD与△BCD,因此由(1)知“翻身后能与原图形重合,故还是能正好落在“锅”中. (3) 如果用来烙饼的铁皮既不是等腰三角形也不是直角三角形 (如图②),那么烙好一面后,怎样将烙饼翻身,才能使烙饼仍能正好落在“锅”中? 解:如图所示,作△ABC 的高AD,把△ABC 分成两个直角三角形,根据(2)中的方法,再作边AB,AC 的中线DE,DF. 因此,共切3刀:AD,DE,DF,或者只切2刀,即只要找出图中的 D点所在的位置,只需切 DE,DF,图中四边形AEDF 是轴对称图形,“翻身”后仍能与原来重合. 12. 在一个三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形吗?证明你的结论. 13,如图,AB=AC=AD. (1) 如果 AD∥BC,那么∠C和∠D有 怎样的数量关系?证明你的结论;解:∠C=2∠D.证明如下: ∵AD∥BC, ∴∠DBC=∠D. ∵AB=AD, ∴∠D=∠ABD,∴∠ABC=2∠D.∵AB=AC,∴∠ABC=∠C.∴∠C=2∠D.(2) 如果∠C=2∠D,那么你能得到 什么结论?证明你的结论解:AD∥BC. 证明如下: ∵AB=AC, ∴∠C=∠ABC=2∠D. ∵AB=AD, ∴∠ABD=∠D.∵∠ABC=2∠D.∴∠CBD=∠D.∴AD∥BC.14. (1) 如图,在△ABC中,∠BAC=90°,AB=AC, 点D在 BC 上且BD=BA,点E在BC的延长线上, 且CE=CA,求∠DAE的度数; (2) 如果把第(1)题中“AB=AC”的条件舍去,其余条件 不变,那么∠DAE的度数会改变吗? 解:∠DAE 的度数不会改变.如图所示.∵BD=BA,∠BAC=90°,∴∠4=∠BAD=90°-∠1.∵CA=CE,∴∠2=∠E.又∵∠4=∠1+∠3, ∠3=∠2+∠E,∴∠3=2∠2,∴∠4=90°-∠1=∠1+2∠2,∴2∠1+2∠2=90°,∴2(∠1+∠2)=90°,∴∠1+∠2=45°,∴∠DAE=45°,∴∠DAE 的度数不会改变.(3) 如果把第(1)题中“∠BAC=90°”的条件改为 “∠BAC=90°”,其余条件不变,那么∠DAE 与∠BAC 有怎样的数量关系? 解:∠BAC 的度数是∠DAE 度数的2倍.如图所示∵BA=BD,∴∠BAD=∠4,∴∠BAC=∠BAD+∠1=∠4+∠1.又∵∠4=∠1+∠3,CA=CE,∴∠2=∠E,∴∠3=2∠2,∴∠BAC=∠1+∠4 = ∠1+∠1+2∠2 =2(∠1+∠2).又∵∠DAE=∠1+∠2.∴∠BAC=2∠DAE.∴∠BAC 的度数是∠DAE 度数的2倍.15. 我们知道:如果点P在线段AB 的垂直平分线l上,那 么PA=PB;如果 PA=PB,那么点P在线段AB 的垂直 平分线l上;如果点P不在线段AB 的垂直平分线l上, 那么 PA≠PB. 试证明:如果 PA≠PB,那么点P不在 线段AB的垂直平分线l上. 证明:假设点P在线段AB的垂直平分线上,由线段垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”得 PA=PB,这与PA≠PB 相矛盾,所以点 P 不在线段AB 的垂直平分线上.16. 已知直线l、点A和点B. 试在直线l上确定一点P,使 PA+PB最小.若点 A,B 在直线l的异侧:如图 4,5,6. 如图2,点A,B到直线的距离相等,线段AB的垂直平分线与直线l的交点为 P,则此时PA+PB最小; 如图 3,点A,B 所在直线垂直于直线l,垂足为P,则此时 PA+PB 最小. 如图 4,5,6,线段 AB 与直线的交点为P,则此时PA+PB 最小.
相关资料
更多









